6.9 Systèmes linéaires non homogènes
Dans cette section, nous traitons du système linéaire non homogène
où la matrice 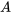 est une fonction matricielle
est une fonction matricielle  et
et 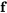 est une fonction de forçage à n vecteurs. Le système homogène associé
est une fonction de forçage à n vecteurs. Le système homogène associé 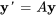 est appelé système complémentaire.
est appelé système complémentaire.
Les méthodes abordées au chapitre 3, à savoir les coefficients indéterminés et la variation des paramètres, utilisées pour trouver des solutions particulières à des équations linéaires non homogènes peuvent être appliquées à des systèmes linéaires non homogènes. Nous nous intéressons ici à la méthode de variation des paramètres.
Variation des paramètres
La méthode de variation des paramètres expliquée à la section 3.5 pour des équations linéaires, s’applique également à des systèmes linéaires. Elle exige un ensemble fondamental de solutions à l’équation complémentaire (homogène).
Théorème. Supposons qu’une matrice 
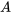 et un vecteur n
et un vecteur n 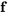 sont continus sur un intervalle ouvert
sont continus sur un intervalle ouvert 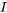 . Disons que
. Disons que 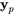 est une solution particulière du système 6.9.1 sur
est une solution particulière du système 6.9.1 sur 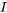 et que
et que 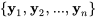 est un ensemble fondamental de solutions du système complémentaire
est un ensemble fondamental de solutions du système complémentaire 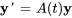 . Alors, la solution générale de l’équation de la section 6.9.1 sur
. Alors, la solution générale de l’équation de la section 6.9.1 sur 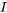 est
est
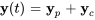
où où 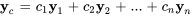 est la solution complémentaire et
est la solution complémentaire et 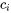 est une constante arbitraire. La solution générale peut donc être exprimée sous la forme
est une constante arbitraire. La solution générale peut donc être exprimée sous la forme
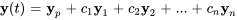
Méthode de variation des paramètres pour des systèmes linéaires non homogènes
Trouver une solution particulière à 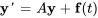
1. Trouver un ensemble fondamental de solutions 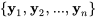 au système complémentaire correspondant
au système complémentaire correspondant 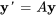 .
.
2. Former la matrice fondamentale 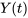 pour le système complémentaire.
pour le système complémentaire.
![Y(t)= [bb(y)_1 \ bb(y)_2 \ ... \ bb(y)_n] Y(t)= [bb(y)_1 \ bb(y)_2 \ ... \ bb(y)_n]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/000d5aec63659080180dd2ddd4ff486d-1.png)
3. Trouver l’inverse de la matrice fondamentale, 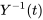 .
.
4. Déterminer 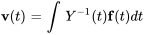
5. Une solution particulière du système est donnée par
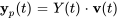
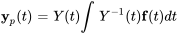
6. Une solution générale du système est donnée par
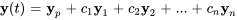
Trouver la solution générale du système
![bb"y"'=[(-4,-3),(6,5)]bb"y"+[(2),(-2e^t)] bb"y"'=[(-4,-3),(6,5)]bb"y"+[(2),(-2e^t)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/c6e69d08fd1d3d681398b2a788d4fc05.png)
Afficher/Masquer la solution
1. Il faut d’abord trouver une solution fondamentale au système complémentaire associé (homogène).
Le polynôme caractéristique de la matrice coefficient 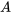 est donné par
est donné par
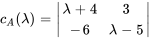
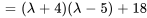

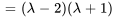
Les racines de 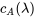 , à savoir
, à savoir 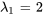 et
et 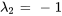 , sont les valeurs propres de
, sont les valeurs propres de 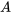 . On trouve ensuite les vecteurs propres correspondants.
. On trouve ensuite les vecteurs propres correspondants.
Pour 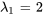 , on a
, on a
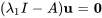
![[(6,3),(-6,-3) ] [(6,3),(-6,-3) ]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/468513c5eb5053861dd8d69a535c0c72.png)
![[(u_1),(u_2)]=[(0),(0)] [(u_1),(u_2)]=[(0),(0)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/e9b1c0442c96e0d85aaf52b869bdcbfa-1.png)
Par conséquent, les vecteurs propres correspondant à 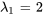 sont
sont ![bb"u"_1=t[(-1),(2)] bb"u"_1=t[(-1),(2)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/cc143b78eb613fd3944af0d7531b3292.png) pour
pour 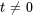 .
.
Pour 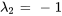 , on a
, on a
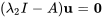
![[(3,3),(-6,-6) ] [(3,3),(-6,-6) ]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/78d2ec3a99ffae4eb51705b0afe0ae7f.png)
![[(u_1),(u_2)]=[(0),(0)] [(u_1),(u_2)]=[(0),(0)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/e9b1c0442c96e0d85aaf52b869bdcbfa-1.png)
Les vecteurs propres correspondant à 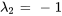 sont
sont ![bb"u"_2=t[(-1),(1)] bb"u"_2=t[(-1),(1)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/d7edd41fab71b4c250b10a63da2cf820-1.png) pour
pour 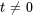 .
.
Par conséquent, ![{e^(2t) [(-1),(2)], \ e^(-t) [(-1),(1)] } {e^(2t) [(-1),(2)], \ e^(-t) [(-1),(1)] }](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/b781a469ccaca3ae4c143b54f811e96f.png) est un ensemble fondamental de solutions au système complémentaire.
est un ensemble fondamental de solutions au système complémentaire.
2. Ainsi, la matrice fondamentale 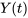 pour le système complémentaire est
pour le système complémentaire est
![Y(t)=[(-e^(2t),-e^-t),(2e^(2t),e^-t)] Y(t)=[(-e^(2t),-e^-t),(2e^(2t),e^-t)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/db7d9dd48e019c4e4fe46cc24f604e40.png)
3. On détermine 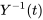
![Y^-1(t)=1/(-e^(2t)e^-t+2e^(2t)e^-t)[(e^(-t),e^-t),(-2e^(2t),-e^(2t))] Y^-1(t)=1/(-e^(2t)e^-t+2e^(2t)e^-t)[(e^(-t),e^-t),(-2e^(2t),-e^(2t))]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/97b5115722fdb5aa28a9f7c54ae636d0.png)
![=[(e^(-2t),e^(-2t)),(-2e^(t),-e^(t))] =[(e^(-2t),e^(-2t)),(-2e^(t),-e^(t))]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/b3dd76be9c70f4eb1b4d795721b4982f.png)
4. On détermine 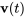 en définissant une constante d’intégration nulle
en définissant une constante d’intégration nulle
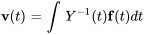
![=int \ [(e^(-2t),e^(-2t)),(-2e^(t),-e^(t))][(2),(-2e^t)] dt =int \ [(e^(-2t),e^(-2t)),(-2e^(t),-e^(t))][(2),(-2e^t)] dt](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/db5570c631ae5d84972b4a025f4cb9f2.png)
![=int \ [(2e^(-2t)-2e^-t),(-4e^t+2e^(2t))] dt =int \ [(2e^(-2t)-2e^-t),(-4e^t+2e^(2t))] dt](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/10e77983c78d601ace074776d5cd0ec4.png)
![=[(-e^(-2t)+2e^-t),(-4e^t+e^(2t))] =[(-e^(-2t)+2e^-t),(-4e^t+e^(2t))]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/7b7c8a66d8666f1770fcb768fa071679.png)
5. Une solution particulière du système est donc donnée par
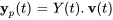
![=[(-e^(2t),-e^-t),(2e^(2t),e^-t)][(-e^(-2t)+2e^-t),(-4e^t+e^(2t))] =[(-e^(2t),-e^-t),(2e^(2t),e^-t)][(-e^(-2t)+2e^-t),(-4e^t+e^(2t))]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/2c9343797188975a44b493cd34dbfd93.png)
![=[(5-3e^t),(-6+5e^t)] =[(5-3e^t),(-6+5e^t)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/2736aea97ed6001185d60c30ede23371.png)
6. Une solution générale du système est donc donnée par
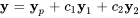
![=[(5-3e^t),(-6+5e^t)] =[(5-3e^t),(-6+5e^t)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/2736aea97ed6001185d60c30ede23371.png)
![+c_1e^(2t) [(-1),(2)] +c_2e^(-t) [(-1),(1)] +c_1e^(2t) [(-1),(2)] +c_2e^(-t) [(-1),(1)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/d786006b25748f15420fa8bb3ec73895.png)
Ce qui peut s’écrire
![bb"y"=[(5-3e^t),(-6+5e^t)] bb"y"=[(5-3e^t),(-6+5e^t)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/74a23b6bb6924cd15c520aeeebda447b.png)
![+[(-e^(2t),-e^-t),(2e^(2t),e^-t)] [(c_1),(c_2)] +[(-e^(2t),-e^-t),(2e^(2t),e^-t)] [(c_1),(c_2)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/3f6e27414ef4c1628576d54d93edeced.png)
Prenons un exemple
Trouver la solution générale du système
![bb(y)'=[(3,14,-13),(0,11,-7),(0,14,-10)]bb(y)+[(2e^t),(0),(-e^(2t))] bb(y)'=[(3,14,-13),(0,11,-7),(0,14,-10)]bb(y)+[(2e^t),(0),(-e^(2t))]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/ce9eb99af0c095407c0add2d74fde843.png)
Afficher/Masquer la solution
Le système complémentaire est
![bb(y)'=[(3,14,-13),(0,11,-7),(0,14,-10)]bb(y) bb(y)'=[(3,14,-13),(0,11,-7),(0,14,-10)]bb(y)](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/5959eac6d6adf680cd1e706a9440ae78.png)
Le vecteur de forçage est
![bb(f)(t)=[(2e^t),(0),(-e^(2t))] bb(f)(t)=[(2e^t),(0),(-e^(2t))]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/61d942657bd581b8e39c47f8da146f1a.png)
1. Dans l’exemple 6.6.3 de la section 6.6, on a trouvé un ensemble fondamental de solutions du système complémentaire associé au système donné dans cet exemple.
![{e^(3t) [(1),(0),(0)], \ e^(4t) [(1),(1),(1)] ,\ e^(-3t)[(2),(1),(2)] } {e^(3t) [(1),(0),(0)], \ e^(4t) [(1),(1),(1)] ,\ e^(-3t)[(2),(1),(2)] }](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/0deb39c7e0345f354db2c992df8d262c.png)
2. La matrice fondamentale 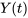 pour le système complémentaire est
pour le système complémentaire est
![Y"(t)=[(e^(3t),e^(4t),2e^(-3t)),(0,e^(4t),e^(-3t) ),(0,e^(4t),2e^(-3t) ) ] Y"(t)=[(e^(3t),e^(4t),2e^(-3t)),(0,e^(4t),e^(-3t) ),(0,e^(4t),2e^(-3t) ) ]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/955c95dc2fcb264e99df1b45dc0ea4b5.png)
3. On détermine 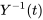 au moyen de la méthode de réduction en lignes, ce qui suppose d’augmenter la matrice
au moyen de la méthode de réduction en lignes, ce qui suppose d’augmenter la matrice 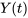 avec la matrice identité.
avec la matrice identité.
![[Y|I]~[I|Y^-1] [Y|I]~[I|Y^-1]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/07daec0952ea2ca5425a61567d9b5830.png)
![Y^-1=[(e^(-3t),0,-e^(-3t)),(0,2e^(-4t),-e^(-4t) ),(0,-e^(3t),e^(3t) ) ] Y^-1=[(e^(-3t),0,-e^(-3t)),(0,2e^(-4t),-e^(-4t) ),(0,-e^(3t),e^(3t) ) ]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/29a939aac4e1fd310744133c97ad4bd6.png)
4. On détermine 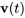 en définissant une constante d’intégration nulle.
en définissant une constante d’intégration nulle.
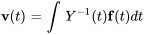
![=int \ [(e^(-3t),0,-e^(-3t)),(0,2e^(-4t),-e^(-4t) ),(0,-e^(3t),e^(3t) ) ] [(2e^t),(0),(-e^(2t))] dt =int \ [(e^(-3t),0,-e^(-3t)),(0,2e^(-4t),-e^(-4t) ),(0,-e^(3t),e^(3t) ) ] [(2e^t),(0),(-e^(2t))] dt](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/c3c28e8a239f5fe70298875f7903eb32.png)
![=int \ [(2e^(-2t)+e^(-t)),(e^(-2t)),(-e^(5t))] dt =int \ [(2e^(-2t)+e^(-t)),(e^(-2t)),(-e^(5t))] dt](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/d1b9e63f7ac25f00fbc016c4d6fc4e62.png)
![=[(-e^(-2t)-e^(-t)),(-1/2e^(-2t)),(-1/5e^(5t))] =[(-e^(-2t)-e^(-t)),(-1/2e^(-2t)),(-1/5e^(5t))]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/d07c3c2515bc74ad35b40da6446c2788.png)
5. Une solution particulière du système est donc donnée par
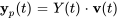
![=[(e^(3t),e^(4t),2e^(-3t)),(0,e^(4t),e^(-3t) ),(0,e^(4t),2e^(-3t) ) ] =[(e^(3t),e^(4t),2e^(-3t)),(0,e^(4t),e^(-3t) ),(0,e^(4t),2e^(-3t) ) ]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/90f921651a5594c31914188221cf488c.png)
![[(-e^(-2t)-e^(-t)),(-1/2e^(-2t)),(-1/5e^(5t))] [(-e^(-2t)-e^(-t)),(-1/2e^(-2t)),(-1/5e^(5t))]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/48ed3e18cd8f3462cba330d7cd2c81a9.png)
![=1/10[(-10e^(t)-19e^(2t)),(-7e^(2t)),(-9e^(2t))] =1/10[(-10e^(t)-19e^(2t)),(-7e^(2t)),(-9e^(2t))]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/a08f2a0ee4bd9960514405bb1a1ba5c7.png)
6. Une solution générale du système est donc donnée par
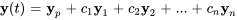
![bb(y)(t)=1/10[(-10e^(t)-19e^(2t)),(-7e^(2t)),(-9e^(2t))] + bb(y)(t)=1/10[(-10e^(t)-19e^(2t)),(-7e^(2t)),(-9e^(2t))] +](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/83549c2ca081dec05d20914cdc9e07ac.png)
![c_1e^(3t) [(1),(0),(0)]+c_2 e^(4t) [(1),(1),(1)]+c_3e^(-3t)[(2),(1),(2)] c_1e^(3t) [(1),(0),(0)]+c_2 e^(4t) [(1),(1),(1)]+c_3e^(-3t)[(2),(1),(2)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/b18254164f9167ab7f262cfd018899e7.png)
Ce qui peut également être exprimé par
![bb"y"=1/10[(-10e^(t)-19e^(2t)),(-7e^(2t)),(-9e^(2t))] bb"y"=1/10[(-10e^(t)-19e^(2t)),(-7e^(2t)),(-9e^(2t))]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/3447c0b1d3cb865a6d89e5f7091ccb5f.png)
![+[(e^(3t),e^(4t),2e^(-3t)),(0,e^(4t),e^(-3t) ),(0,e^(4t),2e^(-3t) ) ] [(c_1),(c_2),(c_3)] +[(e^(3t),e^(4t),2e^(-3t)),(0,e^(4t),e^(-3t) ),(0,e^(4t),2e^(-3t) ) ] [(c_1),(c_2),(c_3)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/ef0f85e6f5d5adb2c08e46d5839defc6.png)
Section 6.9 Exercices
- Trouve la solution générale du système d’équations différentielles
![bb"y'"=[(-25,36),(-18,26)] bb"y" bb"y'"=[(-25,36),(-18,26)] bb"y"](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/0cfb5490807641faadba4c7654f75a2c.png)
![+[(-2),(5 e^t)] +[(-2),(5 e^t)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/404052f200ef1e4c2eaa9517879d2543.png)
Afficher/Masquer la réponse
![bb(y)(t)=[(-26-90 e^t),(-18-65 e^t)]+[(3e^-t,4e^(2t)),(2e^-t,3e^(2t))][(c_1),(c_2)] bb(y)(t)=[(-26-90 e^t),(-18-65 e^t)]+[(3e^-t,4e^(2t)),(2e^-t,3e^(2t))][(c_1),(c_2)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/323ebc77fb623c37f9b254e815489d52.png)
- Trouve la solution générale du système d’équations différentielles
![bb"y'"=[(5,3),(-6,-4)] bb"y" bb"y'"=[(5,3),(-6,-4)] bb"y"](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/e9b37c4ca61fe7d497ec38e25222cef4.png)
![+[(2),(5 e^t)] +[(2),(5 e^t)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/b713ac20cead32f01c8687235006df36.png)
Afficher/Masquer la réponse
![bb(y)(t)=[(-4-7.5 e^t),(6+10 e^t)]+[(-e^-t,-e^(2t)),(2e^-t,e^(2t))][(c_1),(c_2)] bb(y)(t)=[(-4-7.5 e^t),(6+10 e^t)]+[(-e^-t,-e^(2t)),(2e^-t,e^(2t))][(c_1),(c_2)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/a7b1e8b088beea791cfe876b2218cbd6.png)
