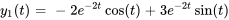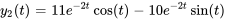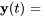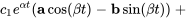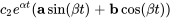6.7 Systèmes homogènes à coefficients constants : valeurs propres complexes
Dans cette section, nous examinons les solutions d’un système homogène à coefficients constants 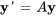 dans les situations où les valeurs propres de la matrice coefficient sont complexes. Normalement, ces valeurs propres sont des conjugués les unes des autres, ce qu’on représente par
dans les situations où les valeurs propres de la matrice coefficient sont complexes. Normalement, ces valeurs propres sont des conjugués les unes des autres, ce qu’on représente par 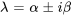 , où
, où  est l’unité imaginaire et
est l’unité imaginaire et 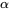 et
et 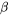 sont des nombres réels. Comme dans le cas complexe d’équations différentielles du second ordre, on utilise la formule d’Euler pour convertir des exponentielles complexes en fonctions trigonométriques réelles, en commençant par la forme de solution supposée
sont des nombres réels. Comme dans le cas complexe d’équations différentielles du second ordre, on utilise la formule d’Euler pour convertir des exponentielles complexes en fonctions trigonométriques réelles, en commençant par la forme de solution supposée 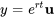 .
.
Théorème. Si une matrice 
 a des valeurs propres complexes conjuguées
a des valeurs propres complexes conjuguées 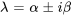 avec le vecteur propre correspondant
avec le vecteur propre correspondant 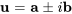 , alors deux solutions linéairement indépendantes du système homogène
, alors deux solutions linéairement indépendantes du système homogène 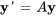 sont
sont
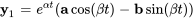
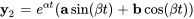
La solution générale du système est donnée par
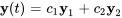
où 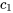 et
et 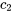 sont des constantes arbitraires.
sont des constantes arbitraires.
Trouver la solution générale de
![bb"y"'=[(5,6),(-3,-1)]bb"y" bb"y"'=[(5,6),(-3,-1)]bb"y"](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/c8d891414eefe9460b3e0389ea7bac01.png)
Afficher/Masquer la solution
1. Il faut d’abord trouver les valeurs propres de  .
.
Le polynôme caractéristique de la matrice coefficient  est donné par
est donné par
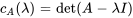
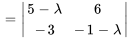

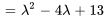
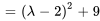
Les racines de 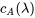 , à savoir
, à savoir 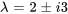 , sont donc les valeurs propres de
, sont donc les valeurs propres de .
.
2. Ensuite, on trouve les vecteurs propres correspondants en trouvant la solution à l’équation 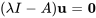 . Cependant, on doit seulement trouver le vecteur propre associé à l’une des valeurs propres, par exemple
. Cependant, on doit seulement trouver le vecteur propre associé à l’une des valeurs propres, par exemple 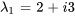 .
.
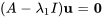
![[(5-(2+i3),6),(-3,-1-(2+i3)) ] [(5-(2+i3),6),(-3,-1-(2+i3)) ]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/89218795ad4da7974d7c6d68cfa23547.png)
![[(u_1),(u_2)]=[(0),(0)] [(u_1),(u_2)]=[(0),(0)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/e9b1c0442c96e0d85aaf52b869bdcbfa.png)
![[(3-i3,6),(-3,-3-i3) ] [(3-i3,6),(-3,-3-i3) ]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/e8d7d3e8e20fc06d41a53d3be509a986.png)
![[(u_1),(u_2)]=[(0),(0)] [(u_1),(u_2)]=[(0),(0)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/e9b1c0442c96e0d85aaf52b869bdcbfa.png)
Pour résoudre le système, on forme la matrice augmentée et on la transforme en FERL au moyen d’opérations de ligne.
![[(3-i3,6,|,0),(-3,-3-i3,|,0) ]~ [(3-i3,6,|,0),(-3,-3-i3,|,0) ]~](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/0fd22ea12ccd2335a6b0c3bdc35250f5.png)
![[(1,1+i,|,0),(0,0,|,0) ] [(1,1+i,|,0),(0,0,|,0) ]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/7dfb7f0199097de96b59e447819c9315.png)
Par conséquent, les vecteurs propres correspondant à la valeur propre 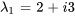 sont
sont ![bb"u"_1=t[(-1-i),(1)] bb"u"_1=t[(-1-i),(1)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/4a6ab4ccacf815527304b48b224d4810.png) pour
pour 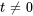 . En prenant
. En prenant 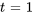 , on a un vecteur propre basique
, on a un vecteur propre basique
![bb"u"_1=[(-1-i),(1)] bb"u"_1=[(-1-i),(1)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/fdf2d97aa65b6dfcc56b377307cfa8de.png)
![=[(-1),(1)]+i[(-1),(0)] =[(-1),(1)]+i[(-1),(0)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/8e615179c467ea665a840025ced8c339.png)
La partie réelle de 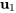 est
est ![bb"a"=[(-1),(1)] bb"a"=[(-1),(1)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/9803cde2a83877319fa2327dd4a8db0a.png) et la partie imaginaire de
et la partie imaginaire de 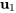 est
est ![bb"b"=[(-1),(0)] bb"b"=[(-1),(0)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/7fba2eacacb5fade842dda019d516791.png) .
.
Le vecteur propre correspondant à la valeur propre conjuguée est le conjugué du vecteur propre 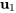 . Ainsi, le vecteur propre associé à la valeur propre
. Ainsi, le vecteur propre associé à la valeur propre 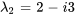 est
est
![bb"u"_2=[(-1+i),(1)] bb"u"_2=[(-1+i),(1)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/cd446a345827152a4156d836e1b66161.png)
![=[(-1),(1)]-i[(-1),(0)] =[(-1),(1)]-i[(-1),(0)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/eacee602b09cda212c1a9963da9c2339.png)
3. Une solution générale du système est donc donnée par l’équation présentée à la section 6.7.1.
![bb"y"(t)=c_1e^(2t)([(-1),(1)] cos(3t)-[(-1),(0)] sin(3 t)) bb"y"(t)=c_1e^(2t)([(-1),(1)] cos(3t)-[(-1),(0)] sin(3 t))](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/cff9331521e60ff25cea6c16a500bcb7.png)
![+c_2e^(2t)([(-1),(1)] sin(3t)+[(-1),(0)] cos(3 t)) +c_2e^(2t)([(-1),(1)] sin(3t)+[(-1),(0)] cos(3 t))](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/556a0db004a12acedd4c3657241c38b4.png)
![=c_1e^(2t)([(-cos(3t)+sin(3t)),(cos(3t))] ) =c_1e^(2t)([(-cos(3t)+sin(3t)),(cos(3t))] )](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/ff278e8dcdb672271f71b40b9b124656.png)
![+c_2e^(2t)([(-sin(3t)-cos(3t)),(sin(3t))] ) +c_2e^(2t)([(-sin(3t)-cos(3t)),(sin(3t))] )](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/6f36a69599e60dc4a30eedeb5a29e2e1.png)
Prenons un exemple
Résoudre le système d’équations différentielles avec des conditions initiales
![bb"y"' = [[1,3],[-15,-11]] \ bb"y", \quad \ bb"y"(0) = [(-3), (12)] bb"y"' = [[1,3],[-15,-11]] \ bb"y", \quad \ bb"y"(0) = [(-3), (12)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/9ea03bc03a2613d22a5a55501fbc4ec7.png) .
.
Afficher/Masquer la solution
1. Il faut d’abord trouver les valeurs propres de  .
.
Le polynôme caractéristique de la matrice coefficient  est donné par
est donné par
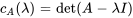
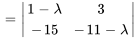
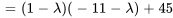
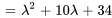
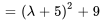
Les racines de 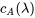 , à savoir
, à savoir 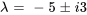 , sont donc les valeurs propres de
, sont donc les valeurs propres de  .
.
2. Ensuite, on trouve les vecteurs propres correspondants en trouvant la solution à l’équation 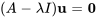 . Cependant, on doit seulement trouver le vecteur propre associé à l’une des valeurs propres, par exemple
. Cependant, on doit seulement trouver le vecteur propre associé à l’une des valeurs propres, par exemple  .
.
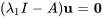
![[(1-lambda,3),(-15,-11-lambda) ] [(1-lambda,3),(-15,-11-lambda) ]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/3e7fc4e133d0be8d400f4223559fc429.png)
![[(u_1),(u_2)]=[(0),(0)] [(u_1),(u_2)]=[(0),(0)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/e9b1c0442c96e0d85aaf52b869bdcbfa.png)
![[(6+i3,3),(-15,-6+i3) ] [(6+i3,3),(-15,-6+i3) ]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/c33227e247cdeed88c250c547c724086.png)
![[(u_1),(u_2)]=[(0),(0)] [(u_1),(u_2)]=[(0),(0)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/e9b1c0442c96e0d85aaf52b869bdcbfa.png)
Pour résoudre le système, on forme la matrice augmentée et on la transforme en FERL au moyen d’opérations de ligne.
![[(6+i3,3,|,0),(-15,-6+i3,|,0) ]~ [(6+i3,3,|,0),(-15,-6+i3,|,0) ]~](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/cdfb259271a0c2e332501ff22b5fdaea.png)
![[(1,2/5-i1/5,|,0),(0,0,|,0) ] [(1,2/5-i1/5,|,0),(0,0,|,0) ]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/c9841b8c82600d6e16eebdba0879e728.png)
Par conséquent, les vecteurs propres correspondant à la valeur propre  sont
sont ![bb"u"_1=t[(-2/5+i1/5),(1)] bb"u"_1=t[(-2/5+i1/5),(1)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/ea439e45144e49f69653e3bd22681513.png) pour
pour 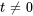 . En prenant
. En prenant 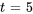 , on a un vecteur propre basique
, on a un vecteur propre basique
![bb"u"_1=[(-2+i),(5)] bb"u"_1=[(-2+i),(5)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/916cf475ef7c412e0bb7f81c2b4867fc.png)
![=[(-2),(5)]+i[(1),(0)] =[(-2),(5)]+i[(1),(0)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/35b6e2905ea2b1196a963c66d65bbfa9.png)
La partie réelle de 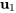 est
est ![bb"a"=[(-2),(5)] bb"a"=[(-2),(5)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/0465306ac322fb9ce9ff4191a59a7be9.png) et la partie imaginaire de
et la partie imaginaire de 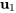 est
est ![bb"b"=[(-1),(0)] bb"b"=[(-1),(0)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/4ad4bddc7597e953d2cada88f1da6144.png) .
.
Le vecteur propre correspondant à la valeur propre conjuguée est le conjugué du vecteur propre 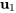 . Ainsi, le vecteur propre associé à la valeur propre
. Ainsi, le vecteur propre associé à la valeur propre  est
est
![bb"u"_1=[(-2+i),(5)] bb"u"_1=[(-2+i),(5)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/fb55221b2a349387f1d899e6716f04f1.png)
![=[(-2),(5)]+i[(1),(0)] =[(-2),(5)]+i[(1),(0)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/46752576acf42e7268d05e16fb266f31.png)
3. Une solution générale du système est donc donnée par l’équation présentée à la section 6.7.1.
![bb"y"(t)=c_1e^(-5t)([(-2),(5)] cos(3t)-[(1),(0)] sin(3 t)) bb"y"(t)=c_1e^(-5t)([(-2),(5)] cos(3t)-[(1),(0)] sin(3 t))](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/93b6584b1852e5e8f23ac282b159166b.png)
![+c_2e^(-5t)([(-2),(5)] sin(3t)+[(1),(0)] cos(3 t)) +c_2e^(-5t)([(-2),(5)] sin(3t)+[(1),(0)] cos(3 t))](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/2810b0b4bd4591fe1ecdd07623f2c9ee.png)
4. On applique les conditions initiales pour trouver les constantes 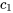 et
et 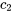 .
.
![bb"y"(0)=[(-3),(12)] bb"y"(0)=[(-3),(12)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/c9d70edadd023c7406587e78d8486529.png)
![c_1e^(0)([(-2),(5)] cos(0)-[(1),(0)] sin(0)) c_1e^(0)([(-2),(5)] cos(0)-[(1),(0)] sin(0))](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/53978b822e69ff07683c48b409131436.png)
![+c_2e^(0)([(-2),(5)] sin(0)+[(1),(0)] cos(0)) = +c_2e^(0)([(-2),(5)] sin(0)+[(1),(0)] cos(0)) =](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/1d10622ee9cb7f731e9549bdc9d359f7.png)
![[(-3),(12)] [(-3),(12)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/f659f82f9f02a1017da1887546b397f3.png)
![c_1[(-2),(5)]+c_2[(1),(0)]= c_1[(-2),(5)]+c_2[(1),(0)]=](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/60d6e74b3ed98e2d751322f15bc831c7.png)
![[(-3),(12)] [(-3),(12)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/f659f82f9f02a1017da1887546b397f3.png)
On obtient ainsi un système de deux équations à deux inconnues.
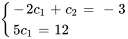
En résolvant le système, on trouve
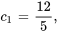
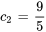
La solution du problème de valeur initiale est donc
![bb"y"(t)=12/5e^(-5t)([(-2),(5)] cos(3t)-[(1),(0)] sin(3 t)) bb"y"(t)=12/5e^(-5t)([(-2),(5)] cos(3t)-[(1),(0)] sin(3 t))](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/8039c5e54662cd3b4c58c9a45c384fb2.png)
![+9/5e^(-5t)([(-2),(5)] sin(3t)+[(1),(0)] cos(3 t)) +9/5e^(-5t)([(-2),(5)] sin(3t)+[(1),(0)] cos(3 t))](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/d9a8e8bcb84901ba366609836cb16d5d.png)
Prenons un exemple
Section 6.7 Exercices
- Trouve une solution au système d’équations différentielles
![bb"y"'=[(-7,-12),(6,5)] bb"y" bb"y"'=[(-7,-12),(6,5)] bb"y"](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/c4550369d47040303fbfc9bfeb86f03a.png)
Afficher/Masquer la réponse
![bb"y"(t)=c_1e^(-t)([(-1),(1)]cos(6t)-[(1),(0)]sin(6t))+ bb"y"(t)=c_1e^(-t)([(-1),(1)]cos(6t)-[(1),(0)]sin(6t))+](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/7b49a7f0bd422ab5ed5d7ae3778dfb1f.png)
![c_2e^(-t)([(-1),(1)]sin(6t)+[(1),(0)]cos(6t)) c_2e^(-t)([(-1),(1)]sin(6t)+[(1),(0)]cos(6t))](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/17ca6af12c361f1fad1b345093985441.png)
- Résoudre le système d’équations différentielles avec des conditions initiales
![bb"y"' = [[4,2],[-29,-10]] \ bb"y", \quad \ bb"y"(0) = [(-2), (19)] bb"y"' = [[4,2],[-29,-10]] \ bb"y", \quad \ bb"y"(0) = [(-2), (19)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/8757c9b230ad0f7ea94e8006bf3047f6.png) .
.Afficher/Masquer la réponse
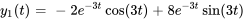
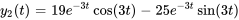
- Résoudre le système d’équations différentielles avec des conditions initiales
![bb"y"' = [[2,1],[-17,-6]] \ bb"y", \quad \ bb"y"(0) = [(-2), (11)] bb"y"' = [[2,1],[-17,-6]] \ bb"y", \quad \ bb"y"(0) = [(-2), (11)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/d7751a6ef3fac4592cb7fc204e2b65e5.png) .
.Afficher/Masquer la réponse