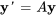6.5 Solutions de systèmes homogènes
A. Ensemble fondamental de solutions et wronskien
Commençons par étudier le système linéaire homogène
où  est une matrice constante
est une matrice constante  à éléments réels et
à éléments réels et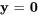 est la solution triviale du système. Toute autre solution est une solution non triviale.
est la solution triviale du système. Toute autre solution est une solution non triviale.
Théorème. Si 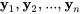 sont
sont  solutions linéairement indépendantes au système présenté dans la section 6.5.1 et
solutions linéairement indépendantes au système présenté dans la section 6.5.1 et  est continue sur un intervalle ouvert
est continue sur un intervalle ouvert 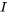 , alors l’ensemble
, alors l’ensemble 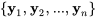 est appelé ensemble fondamental de solutions au système sur
est appelé ensemble fondamental de solutions au système sur 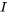 .
.
Comme expliqué à la section 6.2 sur l’indépendance linéaire, les vecteurs 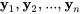 sont linéairement indépendants si
sont linéairement indépendants si 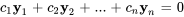 n’a pour solution que la solution triviale. Ainsi, si
n’a pour solution que la solution triviale. Ainsi, si
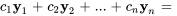
![[[y_11, y_12 ,..., y_(1n)],[y_21,y_22, ..., y_(2n)], [vdots,vdots ,ddots, vdots] ,[y_(n1), y_(n2) , ..., y_(n\n)] ] [[y_11, y_12 ,..., y_(1n)],[y_21,y_22, ..., y_(2n)], [vdots,vdots ,ddots, vdots] ,[y_(n1), y_(n2) , ..., y_(n\n)] ]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/210673bd528f7b46a75654b5191793d8.png)
![[[c_1],[c_2], [vdots] ,[c_n] ]=bb"0" [[c_1],[c_2], [vdots] ,[c_n] ]=bb"0"](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/2b120ae9b191de4d93fb48c7d2ce0379.png)
alors ![bb"c"=[[c_1],[c_2], [vdots] ,[c_n] ]=bb"0" bb"c"=[[c_1],[c_2], [vdots] ,[c_n] ]=bb"0"](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/578b6b9fd0d79d52a0f08f0415c73ee2.png)
Pour que cette solution soit unique, le déterminant de la matrice du coefficient de l’équation dont les colonnes sont les fonctions vectorielles ![[(bb"y"_1,bb"y"_2, ..., bb"y"_n)] [(bb"y"_1,bb"y"_2, ..., bb"y"_n)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/1a2fe1fcf4b963095fb626a316b0791e.png) ne doit pas être nul. Le déterminant de la matrice du coefficient de l’équation est appelé wronskien et transcrit
ne doit pas être nul. Le déterminant de la matrice du coefficient de l’équation est appelé wronskien et transcrit 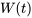 .
.

Théorème. Si le wronkien 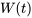 de
de 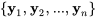 n’est pas nul en un point (et donc jamais nul) sur
n’est pas nul en un point (et donc jamais nul) sur 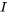 , alors
, alors 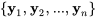 est linéairement indépendant, formant un ensemble fondamental de solutions pour le système présenté à la section 6.5.1 sur
est linéairement indépendant, formant un ensemble fondamental de solutions pour le système présenté à la section 6.5.1 sur 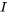 . La matrice fondamentale
. La matrice fondamentale 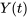 du système est
du système est
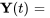
![[(bb"y"_1,bb"y"_2, ..., bb"y"_n)]= [(bb"y"_1,bb"y"_2, ..., bb"y"_n)]=](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/5837101a172e7de88ce571f8e1d4566e.png)
![[[y_11, y_12 ,..., y_(1n)],[y_21,y_22, ..., y_(2n)], [vdots,vdots ,ddots, vdots] ,[y_(n1), y_(n2) , ..., y_(n\n)] ] [[y_11, y_12 ,..., y_(1n)],[y_21,y_22, ..., y_(2n)], [vdots,vdots ,ddots, vdots] ,[y_(n1), y_(n2) , ..., y_(n\n)] ]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/210673bd528f7b46a75654b5191793d8.png)
Étant donné que les fonctions vectorielles
![bb"y"_1=[(-2),(3)]e^(3t) bb"y"_1=[(-2),(3)]e^(3t)](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/1fd5b4549a72bc72f0fdf85446d5ef0e.png) et
et ![bb"y"_2=[(-2),(-1)]e^(t) bb"y"_2=[(-2),(-1)]e^(t)](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/ce30498e8d09c443028da1a1df6ca37a.png)
sont des solutions d’un système à coefficient constant 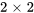 , a) calculer le wronkskien de
, a) calculer le wronkskien de  et b) trouver la solution générale du système.
et b) trouver la solution générale du système.
Afficher/Masquer la solution
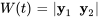
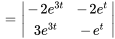
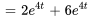
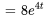
b) Comme 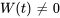 ,
,  sont linéairement indépendants, l’ensemble est un ensemble fondamental de solutions au système et la matrice suivante est la matrice fondamentale du système.
sont linéairement indépendants, l’ensemble est un ensemble fondamental de solutions au système et la matrice suivante est la matrice fondamentale du système.
![Y=[(-2e^(3t),-2e^t),(3e^(3t),-e^t)] Y=[(-2e^(3t),-2e^t),(3e^(3t),-e^t)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/a576b4cafb66b8f1a0074ec88604132b.png)
La solution générale est donc
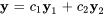
![=c_1[(-2),(3)]e^(3t) =c_1[(-2),(3)]e^(3t)](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/c5afe47b33ed8874b02d56a117021304.png)
![+c_2[(-2),(-1)]e^(t) +c_2[(-2),(-1)]e^(t)](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/89415a04f31518914c703e9f90dbf3ef.png)
![=[(-2e^(3t),-2e^t),(3e^(3t),-e^t)] =[(-2e^(3t),-2e^t),(3e^(3t),-e^t)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/17d51d9f9e97c367634208d7f53f2113.png)
![[(c_1),(c_2)] [(c_1),(c_2)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/9163ee11f687e7de98db610527c319eb.png)
Prenons un exemple
B. Solutions de systèmes homogènes à coefficients constants
Pour trouver les solutions de systèmes homogènes à coefficients constants, représentés par le système présenté à la section 6.5.1, on applique une approche similaire à celle utilisée pour résoudre des équations différentielles linéaires homogènes à coefficients constants.
À la section 3.2, on a trouvé une solution non triviale de la forme  pour une équation différentielle linéaire homogène à coefficients constants. La section 6.4 a montré que toute équation différentielle linéaire d’ordre supérieur peut être exprimée comme un système linéaire d’équations différentielles du premier ordre. Par conséquent, il est raisonnable qu’une solution du système indiqué à la section 6.5.1 présente la forme
pour une équation différentielle linéaire homogène à coefficients constants. La section 6.4 a montré que toute équation différentielle linéaire d’ordre supérieur peut être exprimée comme un système linéaire d’équations différentielles du premier ordre. Par conséquent, il est raisonnable qu’une solution du système indiqué à la section 6.5.1 présente la forme
Ici, 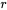 est une constante et
est une constante et 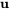 est un vecteur constant. L’étape suivante consiste à remplacer la solution présentée à la section 6.5.2 dans notre système. Ce qui donne
est un vecteur constant. L’étape suivante consiste à remplacer la solution présentée à la section 6.5.2 dans notre système. Ce qui donne
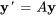
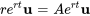
Après avoir annulé le terme exponentiel 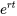 , on arrive à
, on arrive à
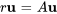
En réarrangeant l’équation, on obtient
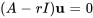
C’est l’équation caractéristique utilisée pour trouver les valeurs propres et les vecteurs propres de la matrice  , comme expliqué à la section 6.3. Pour que la solution que nous avons trouvée
, comme expliqué à la section 6.3. Pour que la solution que nous avons trouvée 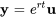 ne soit pas triviale,
ne soit pas triviale, 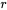 et
et 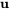 doivent correspondre à la valeur propre et au vecteur propre de la matrice
doivent correspondre à la valeur propre et au vecteur propre de la matrice  , respectivement.
, respectivement.
Ainsi, pour résoudre le système 6.5.1, il faut d’abord trouver les valeurs propres et les vecteurs propres de la matrice coefficient  . La structure de la solution varie selon la nature des valeurs propres, qui peuvent être réelles et distinctes, complexes ou répétées. Chacun de ces scénarios sera exploré dans les sections suivantes.
. La structure de la solution varie selon la nature des valeurs propres, qui peuvent être réelles et distinctes, complexes ou répétées. Chacun de ces scénarios sera exploré dans les sections suivantes.
Section 6.5 Exercices
- Étant donné que les fonctions vectorielles
![bb"y"_1=[(-5),(6)]e^(-t) bb"y"_1=[(-5),(6)]e^(-t)](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/d3f7da196b2cca467e0df2d229fe6c01.png) et
et ![bb"y"_2=[(3),(1)]e^(4t) bb"y"_2=[(3),(1)]e^(4t)](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/5819b83ce59ffa93ac4816e340cfc10e.png)
sont des solutions à un système différentiel à coefficients constants
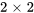 , calcule le wronskien de
, calcule le wronskien de  . Détermine si les vecteurs sont linéairement indépendants.
. Détermine si les vecteurs sont linéairement indépendants.Afficher/Masquer la réponse
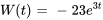 . Les vecteurs sont linéairement indépendants, car leur wronskien n’est jamais nul pour tout nombre réel
. Les vecteurs sont linéairement indépendants, car leur wronskien n’est jamais nul pour tout nombre réel  .
. - Étant donné que les fonctions vectorielles
![bb"y"_1=[(-1),(-1)]e^(4t) bb"y"_1=[(-1),(-1)]e^(4t)](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/0c94f9223a83180a74c18706c1b00479.png) et
et ![bb"y"_2=[(-7),(-2)]e^(-4t) bb"y"_2=[(-7),(-2)]e^(-4t)](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/92435f434d3d68de4b2ee75793dbd2d7.png)
sont des solutions à un système différentiel à coefficients constants
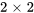 , calcule le wronskien de
, calcule le wronskien de  . Détermine si les vecteurs sont linéairement indépendants.
. Détermine si les vecteurs sont linéairement indépendants.Afficher/Masquer la réponse
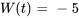 . Les vecteurs sont linéairement indépendants, car leur wronskien n’est pas nul.
. Les vecteurs sont linéairement indépendants, car leur wronskien n’est pas nul.