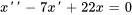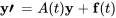6.4 Systèmes linéaires d’équations différentielles
A. Introduction
Après avoir exploré les équations différentielles du premier ordre et du second ordre, intéressons-nous maintenant aux systèmes d’équations différentielles. Ces systèmes permettent de modéliser des scénarios comportant de multiples processus interdépendants, ce qui est courant dans les situations complexes du monde réel.
Par exemple, dans un écosystème où interagissent des espèces comme les proies et les prédateurs, le taux de variation de la population de chaque espèce dépend non seulement de sa taille, mais aussi des populations d’autres espèces. Cette interaction conduit à un système d’équations différentielles, où chaque équation représente le taux de croissance d’une espèce, incarnant leurs interrelations. De même, dans les problèmes de mélanges avec des réservoirs interconnectés, la concentration dans un réservoir affecte et est affectée par les concentrations dans les réservoirs connectés. Dans les systèmes mécaniques, tels qu’un système masse-ressort à multiples masses et ressorts, le déplacement de chaque masse est influencé par ses voisines, formant un système d’équations différentielles interconnectées.
B. Systèmes d’équations différentielles linéaires du premier ordre
Cette section présente la méthode matricielle pour résoudre des systèmes d’équations différentielles linéaires du premier ordre. Ces systèmes sont caractérisés par le fait que chaque équation est du premier ordre et linéaire. Ils peuvent être écrits sous la forme suivante :
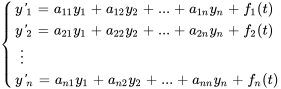
La notation matricielle simplifie la caractérisation et la résolution de ces systèmes, de la même manière que les systèmes d’équations algébriques. Un système linéaire du premier ordre peut être exprimé sous forme de matrice comme suit :
![[[y'_1],[y'_2], [vdots] ,[y'_n] ]= [[y'_1],[y'_2], [vdots] ,[y'_n] ]=](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/ccd697174769ff7d7bdbae8e78cb46af.png)
![[[a_11, a_12 ,..., a_(1n)],[a_21,a_22, ..., a_(2n)], [vdots,vdots ,ddots, vdots] ,[a_(n1), a_(n2) , ..., a_(n\n)] ] [[a_11, a_12 ,..., a_(1n)],[a_21,a_22, ..., a_(2n)], [vdots,vdots ,ddots, vdots] ,[a_(n1), a_(n2) , ..., a_(n\n)] ]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/b3cbeb5023078db66d19fce4b66d8644.png)
![[[y_1],[y_2], [vdots] ,[y_n] ]+ [[y_1],[y_2], [vdots] ,[y_n] ]+](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/ebe315c7d2963a400b4e6697c0b4eb9d.png)
![[[f_1],[f_2], [vdots] ,[f_n] ] [[f_1],[f_2], [vdots] ,[f_n] ]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/1bcff6840b1963b01a8954227bcfaf50.png)
Dans la notation vectorielle, le système est écrit comme suit :
Ici, la matrice 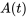 est la matrice coefficient et
est la matrice coefficient et 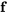 est la fonction vectorielle de forçage.
est la fonction vectorielle de forçage. 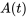 et
et 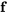 sont continues si leurs éléments sont continus. Si
sont continues si leurs éléments sont continus. Si 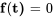 dans l’équation de la section 6.4.1, le système est homogène, sinon, il est non homogène.
dans l’équation de la section 6.4.1, le système est homogène, sinon, il est non homogène.
Un problème de valeur initiale suppose de trouver une solution pour
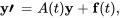
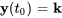 (6.4.2)
(6.4.2)
où 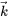 est un vecteur constant représentant la condition initiale.
est un vecteur constant représentant la condition initiale.
![veck=[[k_1],[k_2], [vdots] ,[k_n] ] veck=[[k_1],[k_2], [vdots] ,[k_n] ]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/4e55b4ce0b94d9cb0a7f416f1c0ce1bf.png)
Écrire le système d’équations différentielles donné sous forme matricielle.
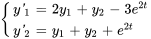
Afficher/Masquer la solution
Le système peut être écrit sous cette forme matricielle :
![[(y'_1),(y'_2)] =[(2,1),(1,1)][(y_1),(y_2)]+[(-3e^(2t)),(e^(2t))] [(y'_1),(y'_2)] =[(2,1),(1,1)][(y_1),(y_2)]+[(-3e^(2t)),(e^(2t))]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/4b1c0d2c3e496d7fdc68dcc0df19b691.png)
![bb (y)'=[(2,1),(1,1)]bb"y"+[(-3),(1)]e^(2t) bb (y)'=[(2,1),(1,1)]bb"y"+[(-3),(1)]e^(2t)](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/6120e29dc4cbba74f61873b7de90daf9.png)
Un problème de valeur initiale pour le système peut être écrit comme ceci :
![bb"y'"=[(2,1),(1,1)]bb"y"+[(-3),(1)]e^(2t), bb"y'"=[(2,1),(1,1)]bb"y"+[(-3),(1)]e^(2t),](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/07d626e19e96d1eb9a92ed9ccc69309f.png)
!["y"(t_0)=[(k_0),(k_1)] "y"(t_0)=[(k_0),(k_1)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/a4808305845881f46225b0164f6cd4da.png)
Prenons un exemple
Théorème d’existence et d’unicité des solutions. Si la matrice coefficient 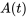 et la fonction de forçage
et la fonction de forçage 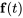 sont continues sur un intervalle ouvert comportant
sont continues sur un intervalle ouvert comportant 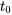 , alors il existe une solution unique au problème de valeur initiale suivant sur cet intervalle.
, alors il existe une solution unique au problème de valeur initiale suivant sur cet intervalle.
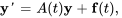
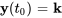
a) Vérifier que
![bb"y"=c_1[(-5),(3)]e^(2t)+c_2[(2),(-1)]e^(t) bb"y"=c_1[(-5),(3)]e^(2t)+c_2[(2),(-1)]e^(t)](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/afc4bd5a77680c0963eb20b1da9e542e.png)
est une solution au système suivant pour n’importe quelles valeurs de 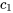 et
et 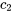 .
.
![bb"y'"=[(-4,-10),(3,7)]bb"y" bb"y'"=[(-4,-10),(3,7)]bb"y"](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/385fbc75d4bb938f7ce19133c59cebfe.png)
b) Trouver la solution de la condition initiale
![bb"y'"=[(-4,-10),(3,7)]bb"y", bb"y'"=[(-4,-10),(3,7)]bb"y",](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/643c5c88ba2fab51b2b10702925c9d9e.png)
![bb"y"(0)=[(1),(-2)] bb"y"(0)=[(1),(-2)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/26b7c7117caffaea4f07062c15efec5f.png)
Afficher/Masquer la solution
a) Si 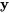 est une solution au système, alors
est une solution au système, alors 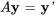 .
.
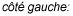
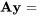
![c_1[(-4,-10),(3,7)][(-5),(3)]e^(2t) c_1[(-4,-10),(3,7)][(-5),(3)]e^(2t)](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/3dbb67690946a8c1e7a9a334e5e54269.png)
![+c_2[(-4,-10),(3,7)] [(2),(-1)]e^(t) +c_2[(-4,-10),(3,7)] [(2),(-1)]e^(t)](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/5f42b9666dfda35ca48c88ea05fdda94.png)
![=c_1[(-10),(6)]e^(2t) =c_1[(-10),(6)]e^(2t)](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/bebc82b97bd9485d63dda5928f55558f.png)
![+c_2[(2),(-1)]e^(t) +c_2[(2),(-1)]e^(t)](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/633798d07769d503f5f35d0e9f0271c3.png)
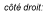
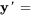
![c_1[(-5),(3)]d/dt( e^(2t))+c_2[(2),(-1)]d/dt( e^(t) ) c_1[(-5),(3)]d/dt( e^(2t))+c_2[(2),(-1)]d/dt( e^(t) )](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/8896748e05e5bb5b7b51793a6802e8ec.png)
![=2c_1[(-5),(3)]e^(2t)+c_2[(2),(-1)]e^(t) =2c_1[(-5),(3)]e^(2t)+c_2[(2),(-1)]e^(t)](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/29d2171b496f5108afbbc6ac248d6d0b.png)
![=c_1[(-10),(6)]e^(2t)+c_2[(2),(-1)]e^(t) =c_1[(-10),(6)]e^(2t)+c_2[(2),(-1)]e^(t)](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/9f458dc36d0a0af01fce1d26d665542f.png)
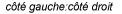
b) Comme la matrice coefficient est continue pour tous les nombres réels 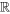 , le théorème d’existence des solutions garantit pour le problème de valeur initiale une solution unique sur
, le théorème d’existence des solutions garantit pour le problème de valeur initiale une solution unique sur 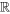 . Pour trouver les constantes
. Pour trouver les constantes 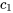 et
et 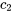 , il faut appliquer la condition initiale :
, il faut appliquer la condition initiale :
![bb"y"(0)=[(1),(-2)] bb"y"(0)=[(1),(-2)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/26b7c7117caffaea4f07062c15efec5f.png)
![c_1[(-5),(3)]e^(0)+c_2[(2),(-1)]e^(0)= c_1[(-5),(3)]e^(0)+c_2[(2),(-1)]e^(0)=](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/e74b4e7534d6bdc93521f813b81c0c60.png)
![[(1),(-2)] [(1),(-2)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/b6c80c345d893aac080a8e1b60cd9c13.png)
![[(-5c_1+2c_2),(3c_1-c_2)]= [(-5c_1+2c_2),(3c_1-c_2)]=](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/f5f2af3a2e2187d0fb629a248d220d7a.png)
![[(1),(-2)] [(1),(-2)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/b6c80c345d893aac080a8e1b60cd9c13.png)
Cela donne un système de deux équations dans deux variables 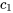 et
et 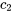 .
.
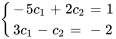
En résolvant le système, on trouve

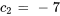
La solution du problème de valeur initiale est donc
![bb(y)=-3[(-5),(3)]e^(2t)-7[(2),(-1)]e^(t) bb(y)=-3[(-5),(3)]e^(2t)-7[(2),(-1)]e^(t)](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/4cd81284cdc89aa2631bb58058ed8526.png)
Prenons un exemple
C. Équation différentielle d’ordren sous forme d’un système de n équations du premier ordre
Les équations différentielles de degré supérieur peuvent être transformées en systèmes d’équations différentielles du premier ordre. Cette conversion permet d’analyser des problèmes complexes d’ordre supérieur à l’aide de techniques et d’outils développés pour les systèmes du premier ordre. Cette approche est largement utilisée dans les méthodes numériques et l’analyse théorique dans diverses applications scientifiques et techniques. Voici un guide étape par étape de ce processus.
Comment convertir des équations différentielles d’ordre 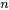 en un système de
en un système de 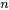 équations du premier ordre
équations du premier ordre
Prenons une équation différentielle linéaire d’ordre 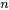 :
:

1. Introduire de nouvelles variables : introduire 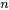 nouvelles variables correspondant à la fonction
nouvelles variables correspondant à la fonction 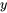 et à ses dérivées jusqu’à l’ordre
et à ses dérivées jusqu’à l’ordre  . Soit
. Soit
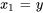
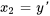
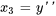
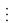
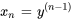
2. Exprimer les dérivées : exprimer les dérivées de ces nouvelles variables en fonction de l’équation différentielle d’origine.
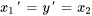
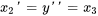
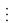
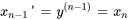
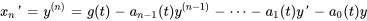
On observe que la dernière équation est l’équation originale réarrangée pour la plus haute dérivée de 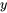 . Dans la dernière équation, remplacer les nouvelles variables par
. Dans la dernière équation, remplacer les nouvelles variables par 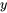 et ses dérivées :
et ses dérivées :

3. Écrire le système d’équations du premier ordre : on a maintenant un système de 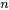 équations différentielles linéaires du premier ordre :
équations différentielles linéaires du premier ordre :
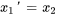
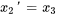
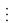
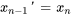

Écrire l’équation différentielle du second ordre donnée sous forme de système d’équations différentielles linéaires du premier ordre
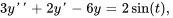
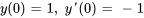
Afficher/Masquer la solution
1. Introduire une nouvelle variable 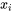 :
:
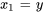
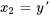
2. Exprimer les dérivées en différenciant les équations ci-dessus et réarranger l’équation différentielle originale afin d’isoler 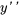 :
:
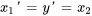
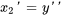
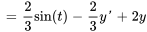

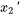
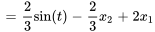
On exprime aussi les conditions initiales par rapport aux nouvelles variables :
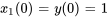
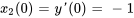
3. Le système d’équations du premier ordre est donc
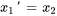
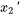
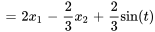
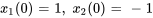
Prenons un exemple
Section 6.4 Exercices
- Écris le système d’équations différentielles donné sous forme matricielle.
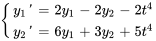
Afficher/Masquer la réponse
![[(y_1'),(y_2')]=[(2,-2),(6,3)][(y_1),(y_2)]+[(-2),(5)]t^4 [(y_1'),(y_2')]=[(2,-2),(6,3)][(y_1),(y_2)]+[(-2),(5)]t^4](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/acdaa2ba77826629fe9d012fdb134d88.png)
- Convertis l’équation différentielle donnée en un système d’équations du premier ordre avec
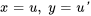 .
.
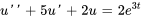
Afficher/Masquer la réponse
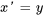
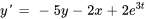
- Réécris le système d’équations linéaires
![[(x'),(y')] = [(3,-5),(2,4)] \ [(x),(y)] [(x'),(y')] = [(3,-5),(2,4)] \ [(x),(y)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/48af37b2f7360f3cd94c24ded9a6052f.png)
sous la forme d’une équation différentielle du second ordre pour
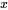 .
.Afficher/Masquer la réponse