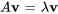6.3 Révision : valeurs propres et vecteurs propres
Il est essentiel de comprendre les valeurs propres et les vecteurs propres pour résoudre des systèmes d’équations différentielles, en particulier pour trouver les solutions de systèmes homogènes. Cette section passe en revue ces concepts et explique comment les trouver.
A. Définition
Considérons une matrice carrée  de taille
de taille  et un vecteur
et un vecteur 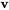 avec
avec 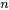 éléments. En multipliant la matrice
éléments. En multipliant la matrice  par le vecteur
par le vecteur 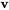 , on obtient un nouveau vecteur
, on obtient un nouveau vecteur 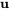 avec
avec 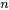 éléments. Géométriquement, cette opération peut être vue comme la transformation du vecteur
éléments. Géométriquement, cette opération peut être vue comme la transformation du vecteur 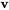 par la matrice
par la matrice  , qui peut impliquer une rotation, une dilatation, une réflexion ou une combinaison de ces éléments, en fonction des propriétés de
, qui peut impliquer une rotation, une dilatation, une réflexion ou une combinaison de ces éléments, en fonction des propriétés de  . Le vecteur
. Le vecteur 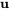 ainsi obtenu peut différer en direction et en magnitude du vecteur original
ainsi obtenu peut différer en direction et en magnitude du vecteur original 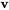 .
.
Dans de nombreuses applications, on recherche un scalaire spécial 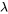 et un vecteur non nul correspondant
et un vecteur non nul correspondant 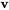 de façon à ce que, lorsque la matrice
de façon à ce que, lorsque la matrice  multiplie
multiplie 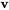 , le résultat soit un scalaire multiple de
, le résultat soit un scalaire multiple de 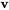 , et non un nouveau vecteur. La relation est exprimée sous la forme
, et non un nouveau vecteur. La relation est exprimée sous la forme
En ce cas, le scalaire 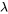 est appelé valeur propre, tandis que le vecteur
est appelé valeur propre, tandis que le vecteur 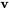 est le vecteur propre de la matrice
est le vecteur propre de la matrice  . Une valeur propre représente donc le facteur par lequel un vecteur propre est dilaté lorsqu’il subit la transformation linaire représentée par
. Une valeur propre représente donc le facteur par lequel un vecteur propre est dilaté lorsqu’il subit la transformation linaire représentée par  .
.
Pour trouver les valeurs propres de la matrice  , il faut résoudre l’équation de la section 6.3.1 pour un
, il faut résoudre l’équation de la section 6.3.1 pour un 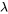 non nul. En réécrivant l’équation, on obtient
non nul. En réécrivant l’équation, on obtient
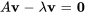
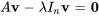
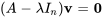
Ici, 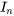 est la matrice identité de la même taille que
est la matrice identité de la même taille que  . Le déterminant de
. Le déterminant de 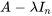 doit être nul pour que ce système ait des solutions non triviales. On définit
doit être nul pour que ce système ait des solutions non triviales. On définit 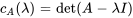 comme lepolynôme caractéristique de la matrice
comme lepolynôme caractéristique de la matrice  . Les racines du polynôme caractéristique sont les valeurs propres, ce qui peut être exprimé sous la forme
. Les racines du polynôme caractéristique sont les valeurs propres, ce qui peut être exprimé sous la forme
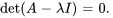 (6.3.2)
(6.3.2)
Une fois les valeurs propres déterminées, les vecteurs propres correspondants sont obtenus en résolvant le système 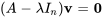 pour chaque valeur propre
pour chaque valeur propre 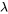 . Ces vecteurs ne sont pas uniques, car tout multiple scalaire d’un vecteur propre est aussi un vecteur propre valide.
. Ces vecteurs ne sont pas uniques, car tout multiple scalaire d’un vecteur propre est aussi un vecteur propre valide.
B. Propriétés des valeurs propres et vecteurs propres
- Multiplicité algébrique : renvoie au nombre de fois où une valeur propre apparaît comme racine dans le polynôme caractéristique d’une matrice. Permet de savoir combien de fois une valeur propre est répétée.
- Multiplicité géométrique : indique le nombre de vecteurs propres linéairement indépendants associés à une valeur propre. La multiplicité géométrique est toujours inférieure ou égale à la multiplicité algébrique.
- Indépendance linéaire des vecteurs propres : les vecteurs propres correspondant à différentes valeurs propres d’une matrice sont linéairement indépendants. Il s’agit d’une propriété essentielle qui permet de former une base dans l’espace vectoriel couvert par ces vecteurs propres. Si les multiplicités algébrique et géométrique d’une valeur propre sont égales, alors il existe un ensemble complet de vecteurs propres linéairement indépendants pour cette valeur propre.
- Valeurs et vecteurs propres conjugués complexes : dans les systèmes qui ont des valeurs propres complexes, ces valeurs propres et leurs vecteurs propres correspondants apparaissent par paires conjuguées. Cela signifie que, si
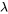 est une valeur propre complexe avec un vecteur propre associé
est une valeur propre complexe avec un vecteur propre associé 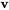 , alors
, alors 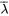 (le conjugué complexe de
(le conjugué complexe de 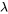 ) est aussi une valeur propre, avec pour vecteur propre correspondant
) est aussi une valeur propre, avec pour vecteur propre correspondant 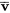 (le conjugué complexe de
(le conjugué complexe de 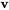 ).
). - Diagonalisation : une matrice est diagonalisable si et seulement si, pour chaque valeur propre, la multiplicité algébrique est égale à la multiplicité géométrique. Cela signifie qu’il y a suffisamment de vecteurs propres linéairement indépendants pour former une base pour l’espace. Si une matrice n’est pas diagonalisable, elle est appelée matrice défectueuse.
Pour la matrice donnée, a) trouver le polynôme caractéristique de la matrice et b) toutes les valeurs propres et leurs vecteurs propres associés.
![A=[(3,5),(1,-1)] A=[(3,5),(1,-1)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/d74d05e7a2fc9b33ae87796160f24505.png)
Afficher/Masquer la solution

![=[(3,5),(1,-1)] -lambda[(1,0),(0,1)] =[(3,5),(1,-1)] -lambda[(1,0),(0,1)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/f80f822493de27f66e3b49135fe0a5d3.png)
![=[(3-lambda,5),(1,-1-lambda) ] =[(3-lambda,5),(1,-1-lambda) ]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/4de0cca10041955f4b0ff7bfdeaeb87d.png)
Le polynôme caractéristique de  est
est
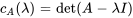
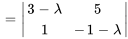
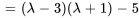
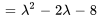
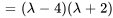
b) Les racines de 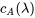 , à savoir
, à savoir 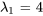 et
et 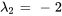 , sont les valeurs propres de
, sont les valeurs propres de  . Pour trouver les vecteurs propres correspondants, il faut trouver la solution du système
. Pour trouver les vecteurs propres correspondants, il faut trouver la solution du système 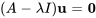 pour chaque valeur propre.
pour chaque valeur propre.
Pour 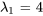 , on a
, on a
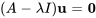
![[(3-lambda_1,5),(1,-1-lambda_1)] [(3-lambda_1,5),(1,-1-lambda_1)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/6ef987f624902a983a183e7b0b8e55a3.png)
![[(u_1),(u_2)]=[(0),(0)] [(u_1),(u_2)]=[(0),(0)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/e9b1c0442c96e0d85aaf52b869bdcbfa.png)
![[(3-4,5),(1,-1-4) ] [(3-4,5),(1,-1-4) ]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/707d89bbf1e3155fe2c65357ab93b0ee.png)
![[(u_1),(u_2)]=[(0),(0)] [(u_1),(u_2)]=[(0),(0)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/e9b1c0442c96e0d85aaf52b869bdcbfa.png)
![[(-1,5),(1,-5) ] [(-1,5),(1,-5) ]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/4fdd357d7663611bd8e8a14ce8a823ab.png)
![[(u_1),(u_2)]=[(0),(0)] [(u_1),(u_2)]=[(0),(0)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/e9b1c0442c96e0d85aaf52b869bdcbfa.png)
Pour résoudre le système, on forme la matrice augmentée et on la transforme en FERL au moyen d’opérations de ligne.
![[(-1,5,|,0),(1,-5,|,0) ] [(-1,5,|,0),(1,-5,|,0) ]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/c7f27a0f136a71e397bacd19f7d93af3.png)
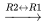
![[(1,-5,|,0),(-1,5,|,0) ] [(1,-5,|,0),(-1,5,|,0) ]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/a8c5ad9a1a1f3f4bd2596159b50628da.png)
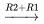 )
) ![[(1,-5,|,0),(0,0,|,0) ] [(1,-5,|,0),(0,0,|,0) ]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/97c2f67c1b292ae52ab2bd38f61f1f63.png)
La deuxième colonne n’a pas de pivot 1, donc 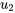 est une variable libre. On représente généralement la variable libre par un paramètre, par exemple
est une variable libre. On représente généralement la variable libre par un paramètre, par exemple  . On écrit alors
. On écrit alors 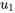 et
et 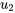 en fonction du paramètre
en fonction du paramètre  .
.
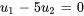
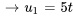
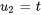
Ainsi, la solution générale est ![bb(u_1)=[(u_1),(u_2)]=t[(5),(1)] bb(u_1)=[(u_1),(u_2)]=t[(5),(1)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/8b126cb4ca21bfcebdc24d9a9435b197.png) , où
, où  est un nombre réel non nul arbitraire. On recherche généralement un vecteur propre basique (sans paramètre). On peut choisir une valeur pour
est un nombre réel non nul arbitraire. On recherche généralement un vecteur propre basique (sans paramètre). On peut choisir une valeur pour  pour trouver un vecteur propre basique. En utilisant
pour trouver un vecteur propre basique. En utilisant 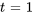 , le vecteur propre correspondant à
, le vecteur propre correspondant à 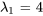 est
est 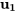
![=[(5),(1)] =[(5),(1)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/945c3e3d85b1cddd3e6489a0aed8ad94.png) .
.
Pour 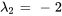 , on a
, on a
![[(3-lambda_2,5),(1,-1-lambda_2)] [(3-lambda_2,5),(1,-1-lambda_2)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/611a138f9809e0247ce43bfc7af8009e.png)
![[(u_1),(u_2)]=[(0),(0)] [(u_1),(u_2)]=[(0),(0)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/e9b1c0442c96e0d85aaf52b869bdcbfa.png)
![[(3+2,5),(1,-1+2) ] [(3+2,5),(1,-1+2) ]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/155fa47df0e5a0de95b157cdeb73d229.png)
![[(u_1),(u_2)]=[(0),(0)] [(u_1),(u_2)]=[(0),(0)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/e9b1c0442c96e0d85aaf52b869bdcbfa.png)
![[(5,5),(1,1) ] [(5,5),(1,1) ]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/3e852eaa6723a3ea234376260d10316a.png)
![[(u_1),(u_2)]=[(0),(0)] [(u_1),(u_2)]=[(0),(0)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/e9b1c0442c96e0d85aaf52b869bdcbfa.png)
Là encore, pour résoudre le système, on forme la matrice augmentée et on la transforme en FERL au moyen d’opérations de ligne.
La solution générale est
![bb(u_2)=[(u_1),(u_2)]=t[(-1),(1)] bb(u_2)=[(u_1),(u_2)]=t[(-1),(1)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/4454399dcd1e61e1538e284fc960e4de.png)
où  est un nombre réel non nul arbitraire. En utilisant
est un nombre réel non nul arbitraire. En utilisant 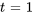 , le vecteur propre basique correspondant à
, le vecteur propre basique correspondant à 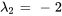 est
est 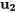
![=[(-1),(1)] =[(-1),(1)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/498f3f35f1049be0a6f6a50ecc2365de.png) .
.
Les deux valeurs propres sont des valeurs propres simples avec une multiplicité algébrique de 1 et, par conséquent, leurs vecteurs propres sont linéairement indépendants.
Prenons un exemple
Pour la matrice donnée, a) trouver le polynôme caractéristique de la matrice et b) toutes les valeurs propres et leurs vecteurs propres associés.
![A=[(-7,-1),(5,-9)] A=[(-7,-1),(5,-9)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/92dde544a0e44c46593b10fa6a3ff8a2.png)
Afficher/Masquer la solution

![=[(-7,-1),(5,-9)] -lambda[(1,0),(0,1)] =[(-7,-1),(5,-9)] -lambda[(1,0),(0,1)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/142265c7f50c7cdc32aa99c4cbf698e7.png)
![=[(-7-lambda,-1),(5,-9-lambda)] =[(-7-lambda,-1),(5,-9-lambda)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/d2783928d985cc6e6ff2304dec57d000.png)
Le polynôme caractéristique de  est
est
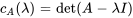
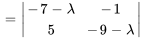
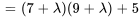
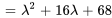
En complétant le carré, on obtient
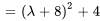
b) Les racines de 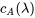 sont les valeurs propres de
sont les valeurs propres de  .
.
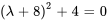
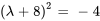
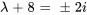
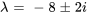
Ensuite, pour trouver les vecteurs propres correspondants, on suit les mêmes étapes que dans l’exemple précédent, en résolvant le système 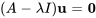 . Cependant, comme les valeurs propres sont des conjugués complexes, leurs vecteurs propres correspondants seront aussi des conjugués. Par conséquent, on doit seulement trouver le vecteur propre associé à l’une des valeurs propres.
. Cependant, comme les valeurs propres sont des conjugués complexes, leurs vecteurs propres correspondants seront aussi des conjugués. Par conséquent, on doit seulement trouver le vecteur propre associé à l’une des valeurs propres.
On trouve le vecteur propre associé à  .
.
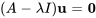
![[(-7-(-8-2i),-1),(5,-9-(-8-2i)) ] [(-7-(-8-2i),-1),(5,-9-(-8-2i)) ]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/ec87112680bc523e491ba8c450510a1a.png)
![[(u_1),(u_2)]=[(0),(0)] [(u_1),(u_2)]=[(0),(0)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/e9b1c0442c96e0d85aaf52b869bdcbfa.png)
![[(1+2i,-1),(5,-1+2i) ] [(1+2i,-1),(5,-1+2i) ]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/e1601a94e659c5eb5a717748fcc93f87.png)
![[(u_1),(u_2)]=[(0),(0)] [(u_1),(u_2)]=[(0),(0)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/e9b1c0442c96e0d85aaf52b869bdcbfa.png)
Pour résoudre le système, on forme la matrice augmentée et on la transforme en FERL au moyen d’opérations de ligne.
![[(1+2i,-1 ,|,0),(5,-1+2i ,|,0) ] [(1+2i,-1 ,|,0),(5,-1+2i ,|,0) ]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/172bc144b97c324bf6fc74cf0afe93fa.png)
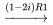 )
) ![[(5,-1+2i ,|,0),(5,-1+2i ,|,0) ] [(5,-1+2i ,|,0),(5,-1+2i ,|,0) ]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/dafb15e6dae4d39c3bd7e25f8bac65dc.png)
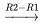
![[(5,-1+2i ,|,0) ,(0,0,|,0) ] [(5,-1+2i ,|,0) ,(0,0,|,0) ]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/962d1b76c8c6dd9f1679c916d2df1277.png)
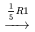 ) »
) » ![[(1,-1/5+2/5i ,|,0) ,(0,0,|,0) ] [(1,-1/5+2/5i ,|,0) ,(0,0,|,0) ]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/2b56063ac13ddd09cd5df5819b10f3f5.png)
La deuxième colonne n’a pas de pivot 1, donc 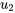 est une variable libre. On représente généralement la variable libre par un paramètre
est une variable libre. On représente généralement la variable libre par un paramètre  . On écrit alors
. On écrit alors 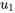 et
et 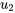 en fonction du paramètre
en fonction du paramètre  .
.
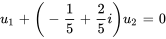
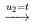 )
)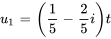
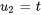
Donc, les vecteurs propres correspondant à la valeur propre  sont
sont ![bb(u_1)=t[(1/5-2/5i ),(1)] bb(u_1)=t[(1/5-2/5i ),(1)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/28c654a0e37af8671a1ed18dabca4afd.png) pour
pour 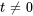 . Avec
. Avec 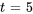 , on a
, on a
![bb(u_1)=[(1-2i),(5)] bb(u_1)=[(1-2i),(5)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/9069c527ffce7cfb3a46fe00e1af06a1.png)
![=[(1),(5)]-i[(2),(0)] =[(1),(5)]-i[(2),(0)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/93313608f4248b67e1e5773f42a6f41a.png)
Le vecteur propre correspondant à la valeur propre conjuguée est le conjugué du vecteur propre 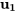 . Ainsi, le vecteur propre associé à la valeur propre
. Ainsi, le vecteur propre associé à la valeur propre  est
est
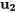
![=[(1+2i),(5)] =[(1),(5)]+i[(2),(0)] =[(1+2i),(5)] =[(1),(5)]+i[(2),(0)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/66c7a07f16a4c8197d6a45c04949d0fd.png)
Les deux valeurs propres sont des valeurs propres simples avec une multiplicité algébrique de 1 et, par conséquent, leurs vecteurs propres sont linéairement indépendants.
Prenons un exemple
Pour la matrice donnée, a) trouver le polynôme caractéristique de la matrice et b) toutes les valeurs propres et leurs vecteurs propres associés.
![A=[(0,6,-2),(0,-2,0),(1,3,-3)] A=[(0,6,-2),(0,-2,0),(1,3,-3)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/881e53e10622ef2b0b8159be78b4d4c0.png)
Afficher/Masquer la solution

![=[(0,6,-2),(0,-2,0),(1,3,-3)] -lambda[(1,0,0),(0,1,0),(0,0,1)] =[(0,6,-2),(0,-2,0),(1,3,-3)] -lambda[(1,0,0),(0,1,0),(0,0,1)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/20463cc54c4241196234c4401dfc8fe1.png)
![=[(-lambda,6,-2),(0,-2-lambda,0) ,(1,3,-3-lambda)] =[(-lambda,6,-2),(0,-2-lambda,0) ,(1,3,-3-lambda)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/36f6d1828b1d58e8b25050b18da0dcc6.png)
Le polynôme caractéristique de  est
est
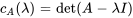
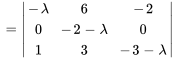
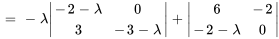
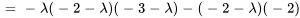
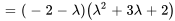
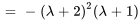
Les racines de 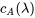 ,
, 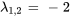 , avec une multiplicité de 2, et
, avec une multiplicité de 2, et 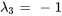 , avec une multiplicité de 1, sont les valeurs propres de
, avec une multiplicité de 1, sont les valeurs propres de  .
.
Pour trouver les vecteurs propres correspondants, il faut trouver la solution du système 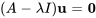 pour chaque valeur propre, comme dans l’exemple précédent.
pour chaque valeur propre, comme dans l’exemple précédent.
Pour 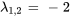 , on a
, on a
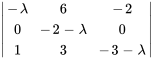
![[(u_1),(u_2),(u_3)]=[(0),(0),(0)] [(u_1),(u_2),(u_3)]=[(0),(0),(0)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/6dc2224125889777fa8b76b924f340f7.png)
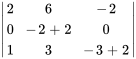
![[(u_1),(u_2),(u_3)]=[(0),(0),(0)] [(u_1),(u_2),(u_3)]=[(0),(0),(0)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/6dc2224125889777fa8b76b924f340f7.png)

![[(u_1),(u_2),(u_3)]=[(0),(0),(0)] [(u_1),(u_2),(u_3)]=[(0),(0),(0)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/6dc2224125889777fa8b76b924f340f7.png)
Pour résoudre le système, on forme la matrice augmentée et on la transforme en FERL au moyen d’opérations de ligne.

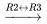 )
) 
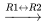

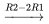

Les deuxième et troisième colonnes n’ayant pas de pivot 1, 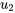 et
et 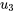 sont des variables libres. On fait en sorte que
sont des variables libres. On fait en sorte que 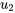 et
et 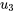 soient représentés par les paramètres
soient représentés par les paramètres 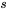 et
et  , respectivement. On écrit alors
, respectivement. On écrit alors 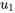 en fonction de ces paramètres.
en fonction de ces paramètres.
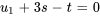
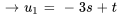
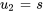
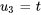
Le vecteur propre 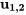 peut donc être exprimé sous la forme
peut donc être exprimé sous la forme
![bb(u_(1,2))=[(u_1),(u_2),(u_3)]=[(-3s+t),(s),(t)] bb(u_(1,2))=[(u_1),(u_2),(u_3)]=[(-3s+t),(s),(t)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/5eb7dda41f187583ddd4cda7782acfec.png)
![=s[(-3),(1),(0)]+t[(1),(0),(1)], =s[(-3),(1),(0)]+t[(1),(0),(1)],](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/8fae2282abafc7021bf4819558871b5f.png)
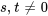 en même temps
en même temps
où 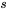 et
et  ne peuvent pas être nuls en même temps, car cela donnerait un vecteur nul et les vecteurs propres ne sont jamais nuls. L’espace propre est traversé par deux vecteurs
ne peuvent pas être nuls en même temps, car cela donnerait un vecteur nul et les vecteurs propres ne sont jamais nuls. L’espace propre est traversé par deux vecteurs ![{[(-3),(1),(0)], \ [(1),(0),(1)]} {[(-3),(1),(0)], \ [(1),(0),(1)]}](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/33ecad6b9640b39a6c959b4dded2c3b2.png) .
.
Les vecteurs propres basiques associés à la valeur propre 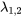 sont donc
sont donc ![bb(u_1)=[(-3),(1),(0)] bb(u_1)=[(-3),(1),(0)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/90a421ec164449e262f65db7fe7f8152.png) et
et ![bb(u_2)= [(1),(0),(1)] bb(u_2)= [(1),(0),(1)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/0904e4682f9649980fb1bd2811d4a26b.png) .
.
Pour 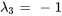 , on a
, on a
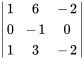
![[(u_1),(u_2),(u_3)]=[(0),(0),(0)] [(u_1),(u_2),(u_3)]=[(0),(0),(0)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/6dc2224125889777fa8b76b924f340f7.png)
Là encore, pour résoudre le système, on forme la matrice augmentée et on la transforme en FERL au moyen d’opérations de ligne.
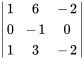
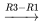 )
) 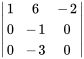
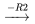
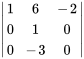
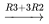 )
)
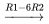

La troisième colonne n’a pas de pivot 1, donc 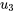 est une variable libre. On représente généralement la variable libre par un paramètre
est une variable libre. On représente généralement la variable libre par un paramètre  . On écrit alors
. On écrit alors 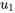 et
et 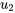 en fonction du paramètre
en fonction du paramètre  .
.
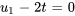
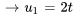
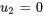
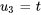
Le vecteur propre 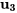 peut ainsi être exprimé sous la forme
peut ainsi être exprimé sous la forme
![bb(u_3)=[(u_1),(u_2),(u_3)]=[(2t),(0),(t)] bb(u_3)=[(u_1),(u_2),(u_3)]=[(2t),(0),(t)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/5485e3cbebd273822649958c01dd7d0d.png)
![=t[(2),(0),(1)], =t[(2),(0),(1)],](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/300b69b36adaae1c44dfde90aef93e62.png)
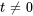
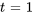 , le vecteur propre correspondant à
, le vecteur propre correspondant à 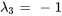 est
est 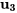
![=[(2),(0),(1)] =[(2),(0),(1)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/aeae6f8f8372c9300c3f9e442f2e4500.png) .
.Pour les deux valeurs propres, la multiplicité algébrique est égale à la multiplicité géométrique et leurs vecteurs propres sont donc linéairement indépendants.
Prenons un exemple
Section 6.3 Exercices
- Trouve les valeurs propres de la matrice
![[(0,-5),(4,6)] [(0,-5),(4,6)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/ddbeb1694f9b15a9a6a780b35c95155a.png) .
.Afficher/Masquer la réponse
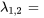
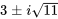
- Trouve les valeurs propres et les vecteurs propres de la matrice
![[(5,2,8),(-4,-1,-16),(0,0,3)] [(5,2,8),(-4,-1,-16),(0,0,3)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/87f33c85ec451b606bccbb123823e68d.png) .
.
Afficher/Masquer la réponse
![lambda_1=1, \ bb(v_1)=[(-1),(2),(0)] lambda_1=1, \ bb(v_1)=[(-1),(2),(0)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/9954daa4b3be8131b181e8aa3bdfb674.png) ou n’importe quel multiple scalaire.
ou n’importe quel multiple scalaire.![lambda_(2,3)=3, \ bb(v_2)=[(-1),(1),(0)], \ bb(v_3)=[(-4),(0),(1)] lambda_(2,3)=3, \ bb(v_2)=[(-1),(1),(0)], \ bb(v_3)=[(-4),(0),(1)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/088d28733e9d2add8c65a34e6a8dff53.png) ou n’importe quel multiple scalaire.
ou n’importe quel multiple scalaire. - Trouve les valeurs propres et les vecteurs propres de la matrice
![[(-5,-4),(14,10)]. [(-5,-4),(14,10)].](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/953e9e4555d90d812a5642717ce90a03.png)
Afficher/Masquer la réponse
![lambda_1=3, \ bb(v_1)=[(1),(-2)] lambda_1=3, \ bb(v_1)=[(1),(-2)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/cd6a3374be1cafd5ceed9426ec9cdbe4.png) ou n’importe quel multiple scalaire.
ou n’importe quel multiple scalaire.![lambda_2=2, \ bb(v_2)=[(4),(-7)] lambda_2=2, \ bb(v_2)=[(4),(-7)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/093ea8ebff350734b07ee92daa2f62c8.png) ou n’importe quel multiple scalaire.
ou n’importe quel multiple scalaire.