6.2 Révision : indépendance linéaire et systèmes d’équations
A. Résolution de systèmes d’équations linéaires
La résolution de systèmes d’équations linéaires est un aspect fondamental de l’algèbre linéaire. Pour résoudre efficacement ces systèmes, on les exprime souvent sous forme matricielle. Prenons un système d’équations linéaires
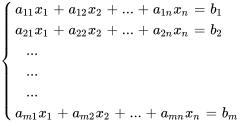
Ce système peut être représenté sous cette forme matricielle
![[[a_11, a_12 ,..., a_(1n)],[a_21,a_22, ..., a_(2n)], [vdots,vdots ,ddots, vdots] ,[a_(m1), a_(m2) , ..., a_(mn)] ] [[a_11, a_12 ,..., a_(1n)],[a_21,a_22, ..., a_(2n)], [vdots,vdots ,ddots, vdots] ,[a_(m1), a_(m2) , ..., a_(mn)] ]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/fd01831660b27cbc3917318d29e7212d.png)
![[[x_1],[x_2], [vdots] ,[x_n] ]= [[x_1],[x_2], [vdots] ,[x_n] ]=](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/d2d7f9db47967f1b580faa26dc51b130.png)
![[[b_1],[b_2], [vdots] ,[b_m] ] [[b_1],[b_2], [vdots] ,[b_m] ]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/776f8619e2ba6d1801963d58a8560cc5.png)
qui est simplement transcrite
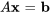
Ici,  est la matrice coefficient comportant les coefficients des variables du système,
est la matrice coefficient comportant les coefficients des variables du système,  est le vecteur (matrice colonne) représentant les variables et
est le vecteur (matrice colonne) représentant les variables et 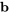 est le vecteur (matrice colonne) représentant les constantes du côté droit de chaque équation. Si tous les termes constants du vecteur
est le vecteur (matrice colonne) représentant les constantes du côté droit de chaque équation. Si tous les termes constants du vecteur 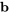 sont nuls, alors le système d’équations linéaires constitue un système homogène. À l’inverse, si une quelconque constante de
sont nuls, alors le système d’équations linéaires constitue un système homogène. À l’inverse, si une quelconque constante de 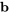 n’est pas nulle, le système est non homogène.
n’est pas nulle, le système est non homogène.
Pour simplifier ce système, on peut utiliser une matrice augmentée, qui combine la matrice coefficient  et le vecteur constant
et le vecteur constant 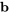 en une seule et même matrice. Il suffit pour ce faire d’ajouter
en une seule et même matrice. Il suffit pour ce faire d’ajouter 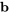 en colonne supplémentaire à
en colonne supplémentaire à  .
.
![[[a_11, a_12 ,..., a_(1n),|,b_1],[a_21,a_22, ..., a_(2n),|,b_2], [vdots,vdots ,ddots, vdots,|,vdots] ,[a_(m1), a_(m2) , ..., a_(mn),|,b_m] ] [[a_11, a_12 ,..., a_(1n),|,b_1],[a_21,a_22, ..., a_(2n),|,b_2], [vdots,vdots ,ddots, vdots,|,vdots] ,[a_(m1), a_(m2) , ..., a_(mn),|,b_m] ]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/8e1016c8e094d7167781189dc97e8c01.png)
On effectue ensuite des opérations de ligne afin de simplifier systématiquement cette matrice augmentée, en préservant l’équivalence du système. Le but est d’obtenir soit une forme échelonnée en lignes (FEL) ou une forme échelonnée réduite en lignes (FERL). La FEL, obtenue grâce à la méthode d’élimination de Gauss, simplifie la matrice en une forme triangulaire supérieure où toutes les lignes non nulles sont situées au-dessus des lignes de tous les zéros et où chaque coefficient principal (premier nombre non nul dans une ligne) est à droite du coefficient principal de la ligne du dessus. La FERL, obtenue grâce à la méthode d’élimination de Gauss-Jordan, simplifie encore la FEL de sorte que chaque coefficient principal est le seul nombre non nul de sa colonne et est égal à 1, ce qui facilite la lecture des solutions directement à partir de la matrice.
Solutions possibles
La solution du système dépend de la forme finale de la matrice augmentée après application des opérations de ligne :
- Solution unique : Si la matrice augmentée peut être réduite à une forme échelonnée en lignes où chaque variable a un coefficient principal 1 et s’il n’y a pas d’équations incohérentes (comme
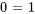 ), alors le système est cohérent et a une solution unique.
), alors le système est cohérent et a une solution unique.
Regarder la vidéo : Solution unique
- Pas de solution : Si la matrice produit une contradiction (comme
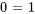 ), alors le système est incohérent et n’a pas de solution.
), alors le système est incohérent et n’a pas de solution.
Regarder la vidéo : Solutions possibles
- Solutions infinies : Si le système a au moins une ligne où tous les coefficients sont nuls, mais que le système est cohérent (comme
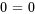 ), alors le système à un nombre infini de solutions. En ce cas, la solution est généralement exprimée sous forme paramétrique. Ce cas se présente normalement lorsqu’il y a moins d’équations indépendantes que de variables.
), alors le système à un nombre infini de solutions. En ce cas, la solution est généralement exprimée sous forme paramétrique. Ce cas se présente normalement lorsqu’il y a moins d’équations indépendantes que de variables.
Regarder la vidéo : Solutions infinies
B. Indépendance linéaire
Il est également important de comprendre le concept d’indépendance linéaire pour résoudre des systèmes d’équations linéaires et d’équations différentielles. Il permet de déterminer si un ensemble de solutions constitue une base valide pour l’espace des solutions et si les solutions sont uniques et couvrent l’ensemble de l’espace des solutions.
Un ensemble de vecteurs dans un espace vectoriel est dit linéairement indépendant si aucun vecteur de l’ensemble ne peut être écrit comme une combinaison linéaire des autres. Considérons un ensemble de vecteurs
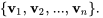
Les vecteurs sont linéairement indépendants si la seule solution à l’équation
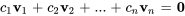
est  , où
, où 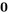 est le vecteur nul et
est le vecteur nul et 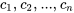 sont des constantes. Autrement dit, aucun des vecteurs ne peut être exprimé sous forme de combinaison linéaire des autres vecteurs. S’il existe au moins une solution non triviale (où tous les
sont des constantes. Autrement dit, aucun des vecteurs ne peut être exprimé sous forme de combinaison linéaire des autres vecteurs. S’il existe au moins une solution non triviale (où tous les 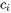 ne sont pas nuls) à cette équation, alors les vecteurs sont linéairement dépendants. Autrement dit, un des vecteurs au moins de l’ensemble peut être écrit comme une combinaison linéaire des autres segments.
ne sont pas nuls) à cette équation, alors les vecteurs sont linéairement dépendants. Autrement dit, un des vecteurs au moins de l’ensemble peut être écrit comme une combinaison linéaire des autres segments.
Pour vérifier l’indépendance ou la dépendance linéaire, on peut représenter ce système sous cette forme matricielle
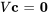
où 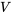 est une matrice dont les colonnes sont les vecteurs de l’ensemble.
est une matrice dont les colonnes sont les vecteurs de l’ensemble.
Test d’indépendance linéaire
- Au moyen d’une matrice : former une matrice
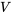 avec ces vecteurs comme colonnes. L’ensemble de vecteurs est linéairement indépendant si le déterminant de
avec ces vecteurs comme colonnes. L’ensemble de vecteurs est linéairement indépendant si le déterminant de 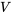 n’est pas nul. Si le déterminant est nul, les vecteurs sont linéairement dépendants.
n’est pas nul. Si le déterminant est nul, les vecteurs sont linéairement dépendants. - Réduction en lignes : réduire les lignes pour donner à la matrice
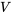 une forme échelonnée en lignes (FEL) ou une forme échelonnée réduite en lignes (FERL). Si une colonne dans
une forme échelonnée en lignes (FEL) ou une forme échelonnée réduite en lignes (FERL). Si une colonne dans 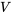 n’a pas de coefficient principal 1 (pivot), les vecteurs sont linéairement dépendants.
n’a pas de coefficient principal 1 (pivot), les vecteurs sont linéairement dépendants.
Si les vecteurs sont ainsi linéairement dépendants, la relation spécifique entre eux peut être déterminée en résolvant le système 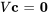 pour les constantes
pour les constantes 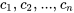 .
.
Déterminer si l’ensemble de vecteurs donné est linéairement indépendant ou dépendant. En cas de dépendance linéaire,trouver la relation exacte entre les vecteurs.
![bb v_1=[(1),( 5),(1)], \ bb v_2=[( -1),( 7),(-1)], \ bb v_3=[( 6),( 0),(9)] bb v_1=[(1),( 5),(1)], \ bb v_2=[( -1),( 7),(-1)], \ bb v_3=[( 6),( 0),(9)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/8a672315642bdbcbaa65a052ea25f27a.png)
Afficher/Masquer la solution
Pour tester l’indépendance linéaire d’un ensemble de vecteurs, il faut d’abord former une matrice avec ces vecteurs en colonnes, puis déterminer si les déterminants sont non nuls.
![V=[[1,-1,6],[5,7,0],[1,-1,9]] V=[[1,-1,6],[5,7,0],[1,-1,9]]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/41b4721fb4b9fac2004ddb716260bedb.png)
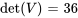
Le déterminant n’est pas nul, donc les vecteurs sont linéairement indépendants.
Déterminer si l’ensemble de vecteurs donné est linéairement indépendant ou dépendant. S’il est dépendant, trouver la relation exacte entre les vecteurs.
![bb v_1=[(5),( 6),(-10)], \ bb v_2=[( 1),( -1),(-2)], \ bb v_3=[( 4),( -2),(-8)] bb v_1=[(5),( 6),(-10)], \ bb v_2=[( 1),( -1),(-2)], \ bb v_3=[( 4),( -2),(-8)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/579c8f4d966d22e0388c77eb8d373a1e.png)
Afficher/Masquer la solution
Pour tester l’indépendance linéaire d’un ensemble de vecteurs, il faut d’abord former une matrice 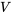 avec ces vecteurs en colonnes
avec ces vecteurs en colonnes
![V=[[5,1,4],[6,-1,-2],[-10,-2,-8]] V=[[5,1,4],[6,-1,-2],[-10,-2,-8]]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/0a3f1607a117aca2d4a8405e66eac902.png)
En calculant le déterminant de 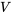 , on trouve
, on trouve
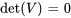
Comme le déterminant est nul, les vecteurs sont linéairement dépendants.
Pour trouver la relation entre les vecteurs, on résout le système 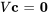 .
.
On forme ensuite la matrice augmentée, puis on réduit les lignes pour la simplifier.
![[[5,1,4,|,0],[6,-1,-2,|,0],[-10,-2,-8,|,0]] [[5,1,4,|,0],[6,-1,-2,|,0],[-10,-2,-8,|,0]]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/ab401bba7e2c50eac1163e4cbc7d787a.png)
En appliquant des opérations de ligne pour donner une forme FERL à la matrice, on obtient
![[[1,0,2/11,|,0],[0,1,34/11,|,0],[0,0,0,|,0]] [[1,0,2/11,|,0],[0,1,34/11,|,0],[0,0,0,|,0]]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/af5881d02157986618fa9b1b9122ac7e.png)
La troisième colonne n’a pas de coefficient principal 1 (pivot), ce qui indique que 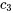 est une variable libre.
est une variable libre.
En convertissant la première ligne de la FERL en équation, on obtient
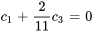

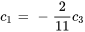
En convertissant la deuxième ligne de la FERL en équation, on obtient
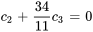

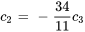
En choisissant 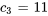 pour simplifier, on trouve
pour simplifier, on trouve
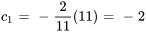
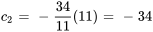
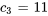
la relation entre les vecteurs de l’ensemble est donc
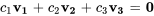
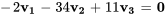
Prenons un exemple
Section 6.2 Exercices
- Résous le système d’équations donné.
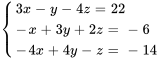
Afficher/Masquer la réponse
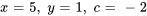
- Détermine si l’ensemble de vecteurs donné est linéairement indépendant en formant une matrice
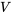 dont les colonnes sont les vecteurs et en calculant le déterminant de
dont les colonnes sont les vecteurs et en calculant le déterminant de 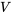 .
.
![bb(v_1)=[(5),( 6),(-10)], \ bb(v_2)=[( 2),( 1),(-4)], \ bb(v_3)=[( -2),( 0),(6)] bb(v_1)=[(5),( 6),(-10)], \ bb(v_2)=[( 2),( 1),(-4)], \ bb(v_3)=[( -2),( 0),(6)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/7a1bcf40e9220baa52784f769b854ad6.png)
Afficher/Masquer la réponse
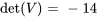
Le déterminant n’étant pas nul, les vecteurs sont linéairement indépendants.
- Détermine si l’ensemble de vecteurs donné est linéairement indépendant en formant une matrice
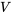 dont les colonnes sont les vecteurs et en calculant le déterminant de
dont les colonnes sont les vecteurs et en calculant le déterminant de 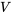 .
.
![bb (v_1)=[(6),( 2),(-18)], \ bb (v_2)=[( 4),( 1),(-12)], \ bb (v_3)=[( 0),( -3),(0)] bb (v_1)=[(6),( 2),(-18)], \ bb (v_2)=[( 4),( 1),(-12)], \ bb (v_3)=[( 0),( -3),(0)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/b1efea50c60c6ea4e9f3c8c6dfe3cfb4.png)
Afficher/Masquer la réponse
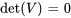
Comme le déterminant est nul, les vecteurs sont linéairement dépendants.
