6.1 Révision : Matrices
L’algèbre linéaire, en particulier l’étude des matrices, est indispensable pour comprendre et résoudre des systèmes d’équations différentielles. Cette section donne un aperçu ciblé des concepts clés de la théorie des matrices.
A. Définition de la matrice et notation
Une matrice est un tableau rectangulaire de nombres, de symboles ou d’expressions, disposés en lignes et en colonnes. Les éléments individuels d’une matrice sont appelés éléments ou entrées. Une matrice est généralement désignée par une lettre majuscule (par exemple, A, B, C). L’élément figurant à la ligne  et la colonne
et la colonne 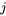 de la matrice A est noté
de la matrice A est noté 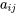 . Les dimensions d’une matrice sont données en
. Les dimensions d’une matrice sont données en 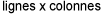 . Par exemple, une matrice A avec
. Par exemple, une matrice A avec 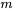 lignes et
lignes et 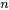 colonnes est une matrice
colonnes est une matrice 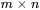 .
.
![A = [[a_11, a_12 ,..., a_(1n)],[a_21,a_22, ..., a_(2n)], [vdots,vdots ,ddots, vdots] ,[a_(m1), a_(m2) , ..., a_(mn)] ]_(mxxn) A = [[a_11, a_12 ,..., a_(1n)],[a_21,a_22, ..., a_(2n)], [vdots,vdots ,ddots, vdots] ,[a_(m1), a_(m2) , ..., a_(mn)] ]_(mxxn)](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/3822e77582622e2a9cc1b0410f5e36f0.png)
B. Matrices spéciales
Une matrice ligne a une seule ligne et plusieurs colonnes, tandis qu’une matrice colonne a une seule colonne et plusieurs lignes Elles sont également dénommées vecteurs ligne et vecteurs colonne, respectivement.
![x = [[a_11, a_12,...,a_(1n)]]_(1xxn) x = [[a_11, a_12,...,a_(1n)]]_(1xxn)](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/4480d0fc4b53f65d7de498d2142ed5bc.png)
![y = [[a_11],[a_(21)], [vdots] ,[a_(m1)] ]_(mxx1) y = [[a_11],[a_(21)], [vdots] ,[a_(m1)] ]_(mxx1)](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/c1001cc07bc48628ec706ab468252ace.png)
Une matrice comportant le même nombre de lignes et de colonnes est une matrice carrée. Par exemple, la matrice B est une matrice carrée  .
.
![B = [[a_11, a_12 ,..., a_(1n)],[a_21,a_22, ..., a_(2n)], [vdots,vdots ,ddots, vdots] ,[a_(n1), a_(n2) , ..., a_(n\n)] ]_(nxxn) B = [[a_11, a_12 ,..., a_(1n)],[a_21,a_22, ..., a_(2n)], [vdots,vdots ,ddots, vdots] ,[a_(n1), a_(n2) , ..., a_(n\n)] ]_(nxxn)](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/1d85735e5cdddfab5b5cb2943c199c3c.png)
Dans une matrice diagonale, les éléments en dehors de la diagonale principale sont tous nuls. La diagonale principale est l’ensemble d’éléments 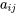 où
où 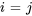 . Par exemple, la matrice C est une matrice diagonale
. Par exemple, la matrice C est une matrice diagonale  .
.
![C = [[a_11, 0 ,..., 0],[0,a_22, ..., 0], [vdots, vdots,ddots, vdots] ,[0, 0 , ..., a_(n\n)] ]_(nxxn) C = [[a_11, 0 ,..., 0],[0,a_22, ..., 0], [vdots, vdots,ddots, vdots] ,[0, 0 , ..., a_(n\n)] ]_(nxxn)](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/b36d57e1a007fe4a5ffa0effc526c9fa.png)
La matrice identité est un type particulier de matrice diagonale, où tous les éléments de la diagonale principale sont des 1. Elle est notée 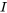 ou
ou 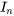 pour indiquer sa taille (
pour indiquer sa taille ( ).
).
![I_n = [[1, 0 ,..., 0],[0,1, ..., 0], [vdots, vdots,ddots, vdots] ,[0, 0 , ..., 1] ]_(nxxn) I_n = [[1, 0 ,..., 0],[0,1, ..., 0], [vdots, vdots,ddots, vdots] ,[0, 0 , ..., 1] ]_(nxxn)](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/15d61a62fbbd3f4322ec761967d6e172.png)
La matrice nulle est une matrice dont tous les éléments sont nuls. Elle est notée 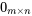 pour indiquer ses dimensions.
pour indiquer ses dimensions.
![0_(mxxn) = [[0, 0 ,..., 0],[0,0, ..., 0], [vdots, vdots,ddots, vdots] ,[0, 0 , ..., 0] ]_(mxxn) 0_(mxxn) = [[0, 0 ,..., 0],[0,0, ..., 0], [vdots, vdots,ddots, vdots] ,[0, 0 , ..., 0] ]_(mxxn)](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/288678af2fe03c972feeae61b6de0482.png)
C. Opérations matricielles
Addition et soustraction de matrices
L’addition et la soustraction de matrices sont des opérations élémentaires qui consistent à additionner ou soustraire des matrices de mêmes dimensions, élément par élément. Si ![A=[a_(ij)] A=[a_(ij)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/b8cb22330fb905bae2aedbf4683f0257.png) et
et ![B=[b_(ij)] B=[b_(ij)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/03f09e9a20341c9c81fc89ffa3850a2d.png) sont des matrices de même taille, leur somme
sont des matrices de même taille, leur somme 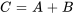 est une matrice dont chaque élément
est une matrice dont chaque élément 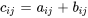 .
.
Ces opérations sont commutatives (c’est-à-dire 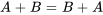 ) et associatives (c’est-à-dire
) et associatives (c’est-à-dire 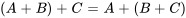 ).
).
Multiplication par un scalaire
La multiplication par un scalaire consiste à multiplier chaque élément d’une matrice par un scalaire (un nombre constant). Si 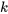 est un scalaire et si
est un scalaire et si ![A=[a_(ij)] A=[a_(ij)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/b8cb22330fb905bae2aedbf4683f0257.png) , alors
, alors 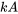 est une matrice dont chaque élément est
est une matrice dont chaque élément est 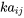 .
.
La multiplication par un scalaire est distributive sur l’addition ou la soustraction de matrices (c’est-à-dire 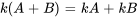 ) et associative par rapport à la multiplication de scalaires (c’est-à-dire
) et associative par rapport à la multiplication de scalaires (c’est-à-dire 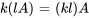 ).
).
Trouver la matrice 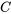 où
où 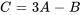 avec les matrices
avec les matrices  et
et 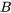 .
.
![A=[[-1,3],[0,7]] A=[[-1,3],[0,7]]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/6ad7c9fc8cd8eabfd44ec2f209c32d00.png) et
et ![B=[[2,-4],[-2,5]] B=[[2,-4],[-2,5]]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/c4d2306d307472b645c49dea09d3af59.png)
Afficher/Masquer la solution
Les matrices  et
et 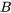 sont de la même taille et peuvent donc être soustraites.
sont de la même taille et peuvent donc être soustraites.
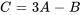
![C=3[[-1,3],[0,7]] -[[2,-4],[-2,5]] C=3[[-1,3],[0,7]] -[[2,-4],[-2,5]]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/0d6525bcc19b4e212d1dc5fbe34bcec9.png)
Il faut d’abord multiplier tous les éléments de la matrice A par 3.
![=[[-3,9],[0,21]] -[[2,-4],[-2,5]] =[[-3,9],[0,21]] -[[2,-4],[-2,5]]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/d84924f8b0a514e3aa946ebebf3c2125.png)
On soustrait ensuite les éléments correspondants.
![=[[-3-2,9-(-4)],[0-(-2),21-5]] =[[-3-2,9-(-4)],[0-(-2),21-5]]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/c8ece06490ea59f699b040b5313fb524.png)
![C=[[-5,13],[2,16]] C=[[-5,13],[2,16]]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/df4ec4e38d075d0184517ea24d641215.png)
Prenons un exemple
Multiplication par un scalaire
La multiplication par un scalaire n’est possible que lorsque le nombre de colonnes dans la première matrice est égal au nombre de lignes dans la deuxième matrice. Prenons deux matrices 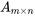 et
et 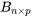 . Le produit de ces matrices donne une nouvelle matrice
. Le produit de ces matrices donne une nouvelle matrice 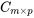 , où la dimension de C est
, où la dimension de C est 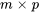 . Chaque élément de C est calculé en prenant le produit scalaire d’une ligne correspondante dans A et d’une colonne correspondante dans B. Le calcul de chaque élément à la ligne
. Chaque élément de C est calculé en prenant le produit scalaire d’une ligne correspondante dans A et d’une colonne correspondante dans B. Le calcul de chaque élément à la ligne  et la colonne
et la colonne 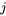 de C est donné par la formule
de C est donné par la formule
La multiplication des matrices est associative, ce qui signifie que 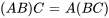 . Elle est aussi distributive sur l’addition, ce qui implique que
. Elle est aussi distributive sur l’addition, ce qui implique que 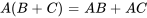 . Cependant, elle n’est pas commutative, de sorte que
. Cependant, elle n’est pas commutative, de sorte que 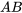 n’est pas nécessairement égal à
n’est pas nécessairement égal à 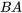 .
.
Les cas particuliers de la multiplication de matrices comprennent les interactions avec les matrices identité et les matrices nulles. La multiplication de n’importe quelle matrice par une matrice identité de taille appropriée laisse la matrice inchangée (c’est-à-dire 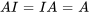 ). N’importe quelle matrice multipliée par une matrice nulle donne une matrice nulle de dimensions appropriées.
). N’importe quelle matrice multipliée par une matrice nulle donne une matrice nulle de dimensions appropriées.
Calculer la matrice 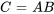 sachant que
sachant que
![A=[[1,4,-1],[2,0,-5]] A=[[1,4,-1],[2,0,-5]]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/55cd6152712bd70d58b73411a0f470e6.png) et
et ![B=[[-7,3,-1,0],[-5,1,4,3],[0,-2,1,2]]. B=[[-7,3,-1,0],[-5,1,4,3],[0,-2,1,2]].](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/1379ee328e4b92fdb9e21e1922295c17.png)
Afficher/Masquer la solution
Pour calculer le produit des matrices A et BT, 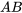 , il faut d’abord s’assurer que la multiplication est possible. La matrice A a les dimensions
, il faut d’abord s’assurer que la multiplication est possible. La matrice A a les dimensions 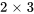 , et la matrice B les dimensions
, et la matrice B les dimensions 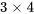 . Comme le nombre de colonnes dans A (3) est égal au nombre de lignes dans B (3), la multiplication peut être effectuée. La matrice C ainsi obtenue aura les dimensions
. Comme le nombre de colonnes dans A (3) est égal au nombre de lignes dans B (3), la multiplication peut être effectuée. La matrice C ainsi obtenue aura les dimensions 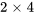 .
.
On calcule chaque élément de la matrice C au moyen de l’équation 6.1.1 :
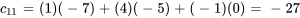
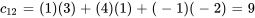
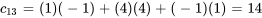
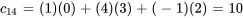
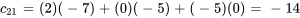
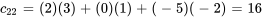
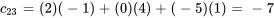
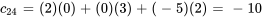
La matrice C obtenue est donc
![C=[[-27,9,14,10],[-14,16,-7,-10]] C=[[-27,9,14,10],[-14,16,-7,-10]]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/dd7e421ae0a982124c0588891df0ecd1.png)
Prenons un exemple
D. Déterminant de matrice
Le déterminant est une valeur scalaire associée à chaque matrice carrée. Il fournit des informations essentielles sur la matrice, telles que son inversibilité. Le déterminant d’une matrice A est noté comme suit
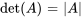
Pour une matrice 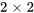 , le déterminant est calculé comme suit :
, le déterminant est calculé comme suit :
Pour les matrices carrées plus grandes, le déterminant est généralement calculé à l’aide de la méthode d’expansion en cofacteurs. Par exemple, le déterminant d’une matrice 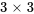 peut être calculé en pratiquant une expansion selon n’importe quelle ligne ou colonne. Pour l’expansion selon la première ligne, la formule est
peut être calculé en pratiquant une expansion selon n’importe quelle ligne ou colonne. Pour l’expansion selon la première ligne, la formule est
Une autre approche du calcul des déterminants, notamment pour les grandes matrices, consiste à utiliser la réduction des lignes pour transformer la matrice en une forme triangulaire supérieure. Le déterminant est alors le produit des éléments diagonaux.
Trouver le déterminant des matrices données.
![A=[[-5,-1],[3,2]] A=[[-5,-1],[3,2]]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/5790881d5a00dcbef515818dc5174f7a.png) et
et ![B= [[2,4,7],[5,-3,8],[0,-1,3] ] B= [[2,4,7],[5,-3,8],[0,-1,3] ]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/86ba0dfd1c8ed0cf775c07c07b11a00a.png)
Prenons un exemple
E. Inverse de matrice
L’inverse d’une matrice carrée  , noté
, noté 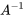 , est une matrice qui, lorsqu’elle est multipliée par
, est une matrice qui, lorsqu’elle est multipliée par  donne la matrice identité.
donne la matrice identité.
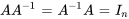
Une méthode courante pour trouver un inverse de matrice consiste à utiliser l’adjointe et le déterminant. La formule est
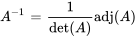
où 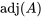 est l’adjointe de
est l’adjointe de  , calculée à partir des cofacteurs de
, calculée à partir des cofacteurs de  . Cette méthode consiste à calculer le déterminant puis la matrice cofacteur, qui est ensuite transposée pour obtenir la matrice adjointe. Pour une matrice
. Cette méthode consiste à calculer le déterminant puis la matrice cofacteur, qui est ensuite transposée pour obtenir la matrice adjointe. Pour une matrice 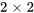 ,
, ![A=[[a_11,a_12],[a_21,a_22]] A=[[a_11,a_12],[a_21,a_22]]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/4274fe78ca6d9f4f0b322cb4aa087d8c.png) , l’inverse est donné par
, l’inverse est donné par
Une autre méthode pour trouver l’inverse est la réduction de ligne, qui suppose d’augmenter la matrice  avec la matrice identité
avec la matrice identité
![[A|I] [A|I]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/d26ef42e744ddaa445ef88eb14213f01.png)
puis à effectuer des opérations sur les lignes pour transformer  en matrice identité. Les opérations permettant de transformer A en
en matrice identité. Les opérations permettant de transformer A en 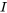 transforment la matrice identité augmentée en
transforment la matrice identité augmentée en 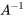 .
.
![[I|A^-1] [I|A^-1]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/9dbdc823b69c59a2bac71a8f5989ac82.png)
Cette méthode est particulièrement utile pour les calculs numériques et les matrices plus grandes.
Si une matrice est inversible, son inverse est unique. Une matrice carrée est inversible si et seulement si elle est non singulière, c’est-à-dire que son déterminant n’est pas nul. Si le déterminant d’une matrice est nul, la matrice n’a pas d’inverse et est alors dite singulière.
Trouver l’inverse de la matrice A, si tant est qu’il existe.
![A=[[4,6],[2,6]] A=[[4,6],[2,6]]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/d07df574ab2124b662937e948d40407c.png)
Afficher/Masquer la solution
Il faut d’abord trouver le déterminant de A pour déterminer si elle a un inverse.
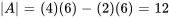
Le déterminant n’étant pas nul, il existe un inverse. Pour une matrice 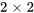 , l’approche des cofacteurs, la formule de la section 6.1.4, est plutôt simple.
, l’approche des cofacteurs, la formule de la section 6.1.4, est plutôt simple.
![A^-1=1/12[[6,-6],[-2,4]] A^-1=1/12[[6,-6],[-2,4]]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/dae4f24454ec630f863c76f36956acd6.png)
![=[[1/2,-1/2],[-1/6,1/3]] =[[1/2,-1/2],[-1/6,1/3]]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/23eeda67ce4b2c52a979adaa70133307.png)
Prenons un exemple
Trouver l’inverse de la matrice A, si tant est qu’il existe.
![A=[[1,0,3],[-3,1,-9],[0,2,1]] A=[[1,0,3],[-3,1,-9],[0,2,1]]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/a709ecf8b6a83a38d2af880b64c7545d.png)
Afficher/Masquer la solution
Pour trouver l’inverse d’une matrice 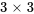 , la méthode de la réduction de ligne est la plus directe. Pour trouver l’inverse de la matrice
, la méthode de la réduction de ligne est la plus directe. Pour trouver l’inverse de la matrice  par la méthode de réduction de ligne, on commence par former une matrice augmentée avec la matrice
par la méthode de réduction de ligne, on commence par former une matrice augmentée avec la matrice  et la matrice identité
et la matrice identité 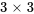
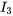 . Le but est d’effectuer des opérations sur les lignes pour transformer le côté gauche de la matrice augmentée (les trois premières colonnes) en matrice identité.
. Le but est d’effectuer des opérations sur les lignes pour transformer le côté gauche de la matrice augmentée (les trois premières colonnes) en matrice identité.
![[A|I]= [A|I]=](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/5325401372ea5b72aaeada54f6f3af71.png)
![[[1,0,3,|,1,0,0],[-3,1,-9,|,0,1,0],[0,2,1,|,0,0,1]] [[1,0,3,|,1,0,0],[-3,1,-9,|,0,1,0],[0,2,1,|,0,0,1]]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/121cf3902cd2a141cd37069f9b42c53a.png)
Effectuer l’opération de ligne :
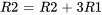 (Ajouter 3 fois la première ligne à la deuxième ligne) :
(Ajouter 3 fois la première ligne à la deuxième ligne) :
![[[1,0,3,|,1,0,0],[0,1,0,|,3,1,0],[0,2,1,|,0,0,1]] [[1,0,3,|,1,0,0],[0,1,0,|,3,1,0],[0,2,1,|,0,0,1]]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/d9d337066d566087f4de0d0ed85ba0e6.png)
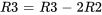 (Soustraire 2 fois la deuxième ligne de la troisième ligne) :
(Soustraire 2 fois la deuxième ligne de la troisième ligne) :
![[[1,0,3,|,1,0,0],[0,1,0,|,3,1,0],[0,0,1,|,-6,-2,1]] [[1,0,3,|,1,0,0],[0,1,0,|,3,1,0],[0,0,1,|,-6,-2,1]]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/5463455d45da23534d698a502a4a1a0e.png)
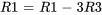 (Soustraire 3 fois la troisième ligne de la première ligne) :
(Soustraire 3 fois la troisième ligne de la première ligne) :
![[[1,0,0,|,19,6,-3],[0,1,0,|,3,1,0],[0,0,1,|,-6,-2,1]] [[1,0,0,|,19,6,-3],[0,1,0,|,3,1,0],[0,0,1,|,-6,-2,1]]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/49d0a39903e06da7c7fad95903465b31.png)
Puisqu’on a réussi à transformer le côté gauche de la matrice augmentée en matrice identité, l’inverse de la matrice A existe et est donné par le côté droit de la matrice augmentée :
![A^-1=[[19,6,-3],[3,1,0],[-6,-2,1]] A^-1=[[19,6,-3],[3,1,0],[-6,-2,1]]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/de9d9d2d34e1628b4b981e8efbcf57aa.png)
Prenons un exemple
F. Calcul matriciel
La différentiation et l’intégration des matrices sont importantes dans le contexte des systèmes d’équations différentielles linéaires, en particulier pour trouver la solution de systèmes non homogènes.
Différenciation matricielle
La différenciation d’une matrice dont les éléments sont des fonctions implique de prendre la dérivée de chaque élément de la matrice individuellement. Considérons la matrice 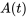 dont les éléments sont une fonction de
dont les éléments sont une fonction de  .
.
![A(t) = [[a_11(t), a_12(t) ,..., a_(1n)(t)],[a_21(t),a_22(t), ..., a_(2n)(t)], [vdots,vdots ,ddots, vdots] ,[a_(m1)(t), a_(m2)(t) , ..., a_(mn)(t) ] ] A(t) = [[a_11(t), a_12(t) ,..., a_(1n)(t)],[a_21(t),a_22(t), ..., a_(2n)(t)], [vdots,vdots ,ddots, vdots] ,[a_(m1)(t), a_(m2)(t) , ..., a_(mn)(t) ] ]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/6e1e8cd5a20fd4abfc96f87adc5a1e39.png)
La dérivée de 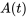 par rapport à
par rapport à  , notée
, notée 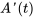 ou
ou 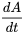 , est une matrice de la même taille dont chaque élément est la dérivée de l’élément correspondant de
, est une matrice de la même taille dont chaque élément est la dérivée de l’élément correspondant de 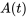 .
.
![A'(t) = [[a'_11(t), a'_12(t) ,..., a'_(1n)(t)],[a'_21(t),a'_22(t), ..., a'_(2n)(t)], [vdots,vdots ,ddots, vdots] ,[a'_(m1)(t), a'_(m2)(t) , ..., a'_(mn)(t)] ] A'(t) = [[a'_11(t), a'_12(t) ,..., a'_(1n)(t)],[a'_21(t),a'_22(t), ..., a'_(2n)(t)], [vdots,vdots ,ddots, vdots] ,[a'_(m1)(t), a'_(m2)(t) , ..., a'_(mn)(t)] ]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/6dea4b2fd091d4ac8bb1c3bc5e4634a2.png)
Les règles standard de différenciation, y compris la règle du produit, la règle du quotient et la règle de la chaîne, s’appliquent à chaque élément de la matrice.
Intégration matricielle
L’intégration d’une matrice avec des éléments qui ont des fonctions est similaire à la différenciation et se fait par éléments. L’intégrale d’une matrice 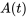 sur une variable
sur une variable  est une matrice de la même taille dont chaque élément est l’intégrale de l’élément correspondant de
est une matrice de la même taille dont chaque élément est l’intégrale de l’élément correspondant de 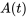 .
.
![intA(t)dt = [[inta_11(t)dt, inta_12(t)dt ,..., inta_(1n)(t)dt],[inta_21(t)dt,inta_22(t)dt, ..., inta_(2n)(t)dt], [vdots,vdots ,ddots, vdots] ,[inta_(m1)(t)dt, inta_(m2)(t)dt , ..., inta_(mn)(t)dt ] ] intA(t)dt = [[inta_11(t)dt, inta_12(t)dt ,..., inta_(1n)(t)dt],[inta_21(t)dt,inta_22(t)dt, ..., inta_(2n)(t)dt], [vdots,vdots ,ddots, vdots] ,[inta_(m1)(t)dt, inta_(m2)(t)dt , ..., inta_(mn)(t)dt ] ]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/a69188820d8bc3b4651e71bf65c1a4a1.png)
Évaluer l’intégrale de la matrice 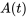 par rapport à
par rapport à  .
.
![A(t) = [(4 e^(4t) , 3te^(-t^2)) , (t^2cos(-3t^3) , -5t^7)] A(t) = [(4 e^(4t) , 3te^(-t^2)) , (t^2cos(-3t^3) , -5t^7)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/e260d44aa8962acbcfca944b87561594.png)
Afficher/Masquer la solution
L’intégrale de matrices est une opération qui s’effectue par éléments.
![intA(t)dt=[intA_(ij)(t)dt] intA(t)dt=[intA_(ij)(t)dt]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/fb91f39a2056595334eae944258f2529.png)
![=[(int4 e^(4t) dt, int3te^(-t^2)dt) , (intt^2cos(-3t^3)dt , int-5t^7dt)] =[(int4 e^(4t) dt, int3te^(-t^2)dt) , (intt^2cos(-3t^3)dt , int-5t^7dt)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/f1c6b4f5306a593ff3b874f5b9804f42.png)
![=[(e^(4t) , -3/2e^(-t^2)) , (-1/9sin(-3t^3) , -5/8t^8)] =[(e^(4t) , -3/2e^(-t^2)) , (-1/9sin(-3t^3) , -5/8t^8)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/50141623c3722d9c48bd8303ee2119b1.png)
Prenons un exemple
Section 6.1 Exercices
- Étant donné que
![A = [(0,-3,3),(3,4,-3)] A = [(0,-3,3),(3,4,-3)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/9c7f56b004d3b9448921f07fbd3462ce.png) et
et ![B = [(-4,0,-4),(-3,0,0)] B = [(-4,0,-4),(-3,0,0)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/95aa11af9c8a881c3754d1730352c887.png) , trouve la matrice
, trouve la matrice 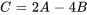 .
.
Afficher/Masquer la réponse
![C=[(16,-6,22),(18,8,-6)] C=[(16,-6,22),(18,8,-6)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/933567a6b900f6463406f0a8ff69f2fb.png)
- Trouve l’inverse de
![A = [(-8,3),(21,-8)] A = [(-8,3),(21,-8)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/8ca06309b54ecd2ae6eed2138a520042.png) .
.
Afficher/Masquer la réponse
![A^-1=[(-8,-3),(-21,-8)] A^-1=[(-8,-3),(-21,-8)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/8d91dc28a86a262c2cc118705da3f82a.png)
- Trouve l’inverse de
![A = [(3,2,0),(1,1,0),(-2,-4,1)]. A = [(3,2,0),(1,1,0),(-2,-4,1)].](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/f80f4c1e98677cc5f6a6e40e74b0bb53.png)
Afficher/Masquer la réponse
![A^-1=[(1,-2,0),(-1,3,0),(-2,8,1)] A^-1=[(1,-2,0),(-1,3,0),(-2,8,1)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/e8431e8128873efe5cc9d3e68fc9db33.png)
- Étant donné les matrices
![A=[(5,-5),(-2,-4)] A=[(5,-5),(-2,-4)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/0ff891b46255ec44d23ca47143f01224.png) et
et ![B=[(-2,1),(4,4)] B=[(-2,1),(4,4)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/9f58131b885d5330d7042f85dc67f65f.png) , trouve leur multiplication
, trouve leur multiplication 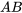 .
.
Afficher/Masquer la réponse
![AB=[(-30,-15),(-12,-18)] AB=[(-30,-15),(-12,-18)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/f76e039cfee5d994aa88a388a7d28eac.png)
- Étant donné la matrice
![A(t) = [(-2 e^(4t) , 3te^(-3t^2)) , (-5tsin(4t^2) , -7t^-5)] A(t) = [(-2 e^(4t) , 3te^(-3t^2)) , (-5tsin(4t^2) , -7t^-5)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/029f698df95cca3a671f439f947c3a7a.png)
Évaluer l’intégrale de
 par rapport à
par rapport à  .
.Afficher/Masquer la réponse
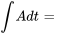
![[(-1/2 e^(4t) , -1/2e^(-3t^2)) , (5/8cos(4t^2) , 7/4t^-4)] [(-1/2 e^(4t) , -1/2e^(-3t^2)) , (5/8cos(4t^2) , 7/4t^-4)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/4c148808d817bdb08a167f798b55340b.png)

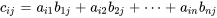
![|[a_11,a_12],[a_21,a_22]|=a_11a_22-a_21a_12 |[a_11,a_12],[a_21,a_22]|=a_11a_22-a_21a_12](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/059bb8efcaa1352ddcb141d23f141548.png)
![|[a_11,a_12,a_13],[a_21,a_22,a_23] ,[a_31,a_32,a_33] |= |[a_11,a_12,a_13],[a_21,a_22,a_23] ,[a_31,a_32,a_33] |=](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/d1d2577b861992088ee3fe65b7ef1eec.png)
![a_11|[a_22,a_23],[a_32,a_33]|- a_11|[a_22,a_23],[a_32,a_33]|-](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/544a2b797fe7ffbd5ec378f9d7aa74c6.png)
![a_12|[a_21,a_23],[a_31,a_33]|+ a_12|[a_21,a_23],[a_31,a_33]|+](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/6f19b481453b02652e1ed57c1a6c09b8.png)
![a_13|[a_21,a_22],[a_31,a_32]| a_13|[a_21,a_22],[a_31,a_32]|](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/053e38ea50ac7f1572e2347f7f06def1.png)
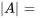
![|[-5,-1],[3,2]|=(-5)(2)-(3)(-1)=-7 |[-5,-1],[3,2]|=(-5)(2)-(3)(-1)=-7](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/2a47204968c0b6afa32c304d114d7357.png)
![|B|=|[2,4,7],[5,-3,8] ,[0,-1,3] |= |B|=|[2,4,7],[5,-3,8] ,[0,-1,3] |=](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/88f3bc20d396330811bd6d46a116d0c9.png)
![2|[-3,8],[-1,3]|- 2|[-3,8],[-1,3]|-](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/79d712b0d3e15837647e4212743c9080.png)
![4|[5,8],[0,3]|+ 4|[5,8],[0,3]|+](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/027a886f0c149a2b807840a695185439.png)
![7|[5,-3],[0,-1]| 7|[5,-3],[0,-1]|](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/bde87f849885fb920e0102553729e0e3.png)
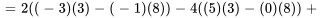
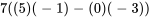
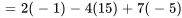
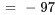
![A^-1=1/(det(A))[[a_22,-a_12],[-a_21,a_11]] A^-1=1/(det(A))[[a_22,-a_12],[-a_21,a_11]]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/db2c539a1405333a0d7c3939a1452ec4.png)