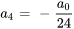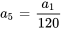5.1 Étude des séries de puissances
Les équations différentielles n’ont pas toutes des solutions qui peuvent être exprimées en termes de fonctions élémentaires telles que des polynômes, des exponentielles, des fonctions trigonométriques, etc. Même lorsque c’est le cas, la recherche explicite de ces solutions peut se révéler complexe, voire impossible. Les solutions de séries permettent de représenter la solution sous la forme d’une somme infinie de termes. Elles peuvent fournir des indications sur le comportement des solutions, notamment leur convergence, leur oscillation ou leurs propriétés de croissance lorsqu’aucune solution explicite n’est connue. Dans les applications pratiques, une solution exacte peut ne pas être nécessaire, et une série finie (une troncature de la série infinie) peut servir de solution approximative. Cette méthode est particulièrement utile dans les méthodes de calcul et les simulations.
Avant d’aborder les solutions d’équations différentielles en séries de puissances, examinons de plus près le concept de série de puissances et ses propriétés pertinentes.
A. Séries de puissances
Une série de puissances est une série infinie de la forme
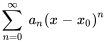
où 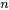 est l’indice de sommation,
est l’indice de sommation, 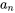 représente le coefficient du terme d’ordre n,
représente le coefficient du terme d’ordre n, 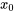 est le centre de la série et
est le centre de la série et 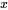 est la variable. La série peut être exprimée comme suit :
est la variable. La série peut être exprimée comme suit :
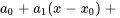
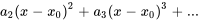
Cela nous permet d’approximer des fonctions dans les régions où la série converge, ce qui est essentiel pour comprendre et résoudre les équations différentielles. Nous pouvons parfois nous intéresser au modèle ou à la forme des termes initiaux de la série ou par la manipulation de termes tels que la réindexation ou la combinaison de termes. Nous pouvons donc « retirer » ces termes de la notation générale de la série.
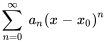
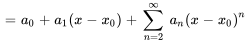
Ici, les deux premiers termes sont retirés de la notation générale de la série et l’indice de sommation commence désormais à 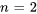 .
.
B. Déplacement de l’indice d’une série de puissances
Le déplacement de l’indice d’une série de puissances modifie le point de départ de la sommation et réindexe les termes de la série. C’est particulièrement utile pour aligner les termes lors de l’addition ou de la soustraction de séries. Considérons une série de puissances
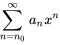
Déplacement à droite (indice croissant)
Pour déplacer la série à droite de 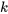 unité, il faut remplacer
unité, il faut remplacer 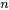 par
par  dans le terme général et ajouter
dans le terme général et ajouter 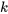 à la limite inférieure d’origine de la sommation.
à la limite inférieure d’origine de la sommation.
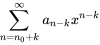
Déplacement à gauche (indice décroissant)
Pour déplacer la série de 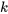 unité, il faut remplacer
unité, il faut remplacer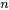 par
par  dans le terme général et soustraire
dans le terme général et soustraire 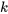 de la limite inférieure d’origine de la sommation.
de la limite inférieure d’origine de la sommation.
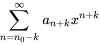
C. Combinaison linéaire de séries de puissances
Lorsque l’on résout des équations différentielles à l’aide de séries, il est souvent nécessaire d’ajouter ou de soustraire des séries. Lors de l’addition ou de la soustraction de séries, il faut s’assurer que les termes ajoutés ou soustraits correspondent à la même puissance de la variable. Autrement dit, il faut s’assurer que les deux séries ont la même puissance de 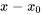 et que leurs indices de sommation sont correctement alignés à partir de la même limite inférieure. Considérons deux séries de puissances
et que leurs indices de sommation sont correctement alignés à partir de la même limite inférieure. Considérons deux séries de puissances
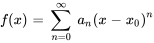 et
et 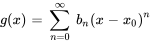
Comme la puissance du terme 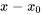 est la même dans les deux séries et que, dans les deux, l’indice commence à la même valeur, elles peuvent être linéairement combinées en
est la même dans les deux séries et que, dans les deux, l’indice commence à la même valeur, elles peuvent être linéairement combinées en
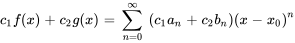
où 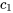 et
et 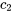 sont des constantes.
sont des constantes.
S’il y a un terme 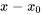 devant la sommation d’une série, on le déplace à l’intérieur de la sommation et on le combine avec le terme
devant la sommation d’une série, on le déplace à l’intérieur de la sommation et on le combine avec le terme 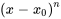 . Par exemple,
. Par exemple,
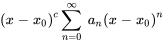
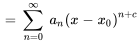
Cela simplifie la gestion et la manipulation des séries dans les solutions d’équations différentielles.
Écrire ce qui suit sous la forme d’une série unique en termes de 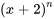 .
.
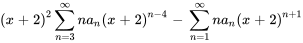
Afficher/Masquer la solution
1. D’abord, on multiplie le terme 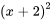 dans la première sommation.
dans la première sommation.
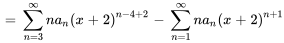
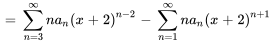
2. Ensuite, on déplace les indices dans les deux séries de façon à ce que l’exposant de 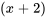 soit
soit 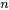 . On peut ainsi déplacer la première série de deux unités sur la gauche et la seconde série d’une unité sur la droite.
. On peut ainsi déplacer la première série de deux unités sur la gauche et la seconde série d’une unité sur la droite.
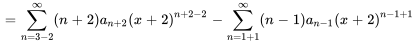
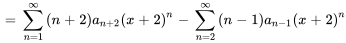
3. Enfin, on s’assure que les deux séries commencent à la même limite inférieure. Selon la série, on peut parfois retirer des termes ou ajuster l’indice si les termes précédents sont déjà nuls. Il convient de noter que, si la seconde série commence à 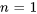 , le terme initial sera nul en raison du facteur
, le terme initial sera nul en raison du facteur  . Par conséquent, le fait de faire commencer l’indice à
. Par conséquent, le fait de faire commencer l’indice à 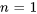 ne modifie en rien sa valeur globale.
ne modifie en rien sa valeur globale.
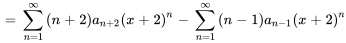
On combine maintenant les séries afin d’obtenir une seule et unique réponse finale.
![=somme_(n=1)^oo [(n+2)a_(n+2)-(n-1)a_(n-1)] (x+2)^(n) =somme_(n=1)^oo [(n+2)a_(n+2)-(n-1)a_(n-1)] (x+2)^(n)](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/73afff9b9536860c6906d1b4b066784c-1.png)
Remarque : en général, quand une série contient un facteur de  , le terme à
, le terme à 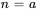 (où a est l’indice de départ) sera nul.
(où a est l’indice de départ) sera nul.
Prenons un exemple
D. Convergence de séries de puissances
La convergence des séries de puissances est essentielle pour garantir que la série représente la fonction avec précision sur un certain intervalle. Une série converge en un point particulier si la somme s’approche d’une limite finie lorsque 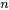 s’approche de l’infini. Autrement dit, une série de puissances converge pour un
s’approche de l’infini. Autrement dit, une série de puissances converge pour un 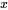 donné si la limite suivante existe.
donné si la limite suivante existe.
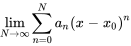
Pour toute série de puissances, l’un ou l’autre des trois cas suivants peut être vrai :
- Converge uniquement en
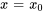 : ici, la somme des séries est égale à
: ici, la somme des séries est égale à 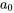 .
. - Converge pour toutes les valeurs de
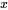 .
. - Converge dans un rayon de convergence
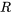 : la série converge si
: la série converge si 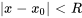 et diverge si
et diverge si 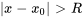 .
. 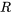 est appelé rayon de convergence et l’intervalle
est appelé rayon de convergence et l’intervalle 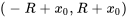 est l’intervalle de convergence.
est l’intervalle de convergence.
Pour déterminer le rayon et l’intervalle de convergence d’une série de puissances donnée, on utilise souvent le test de ratio. Le test de ratio consiste à prendre la limite
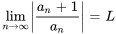
Si 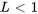 , la série converge et le rayon de convergence est
, la série converge et le rayon de convergence est 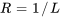 .
.
E. Différenciation de séries de puissances
La différenciation et l’intégration des séries de puissances dans leur intervalle de convergence peuvent être effectuées terme par terme. Pour une série de puissances donnée centrée en 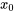
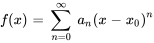
La dérivée première de 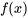 est
est
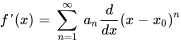
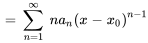
Notez que l’indice de la dérivée première commence à 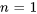 , car le premier terme de la série originale est constant (
, car le premier terme de la série originale est constant (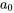 ) et disparaît lors de la différenciation. L’intervalle de convergence de la série dérivée est au moins aussi grand que celui de la série originale, mais une attention particulière doit être portée aux extrémités.
) et disparaît lors de la différenciation. L’intervalle de convergence de la série dérivée est au moins aussi grand que celui de la série originale, mais une attention particulière doit être portée aux extrémités.
De même, la dérivée seconde de 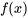 est
est
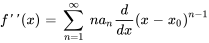
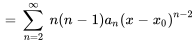
Notez que l’indice de la dérivée seconde commence à 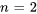 , car le premier terme de la dérivée première est constant (
, car le premier terme de la dérivée première est constant (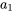 ) et disparaît lors de la différenciation.
) et disparaît lors de la différenciation.
Supposons que 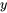 peut être exprimé sous la forme d’une série de puissances
peut être exprimé sous la forme d’une série de puissances 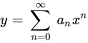 . Écrire ce qui suit sous la forme d’une seule série en termes de
. Écrire ce qui suit sous la forme d’une seule série en termes de 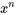 .
.
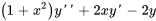
Afficher/Masquer la solution
1. Il faut d’abord trouver 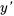 et
et 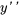 :
:
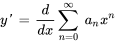
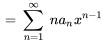
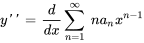
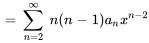
2. Ensuite, on remplace 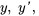 et
et 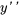 dans l’expression :
dans l’expression :
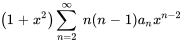
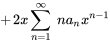
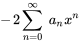
3. En multipliant le terme 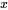 devant la sommation par le terme
devant la sommation par le terme 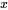 dans le terme général de chaque série, on obtient
dans le terme général de chaque série, on obtient
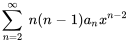
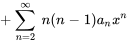
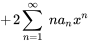
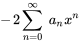
4. On observe que l’exposant de 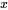 est le même dans toutes les séries sauf dans la première. Il suffit donc de décaler l’indice des premières sommations de 2 vers la gauche :
est le même dans toutes les séries sauf dans la première. Il suffit donc de décaler l’indice des premières sommations de 2 vers la gauche :
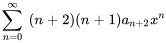
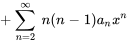
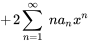
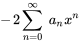
5. Enfin, on s’assure que toutes les séries partent de la même limite inférieure Remarquez que la deuxième série est nulle à 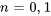 parce qu’il y a des facteurs
parce qu’il y a des facteurs 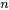 et
et  dans le terme général de la série. Ainsi, son indice peut commencer à
dans le terme général de la série. Ainsi, son indice peut commencer à 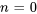 sans changer de valeur. Pareillement, la troisième série est nulle à
sans changer de valeur. Pareillement, la troisième série est nulle à 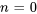 , de sorte qu’elle peut aussi commencer à
, de sorte qu’elle peut aussi commencer à 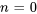 . On réécrit donc les indices pour obtenir
. On réécrit donc les indices pour obtenir
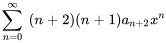
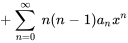
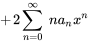
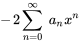
En combinant les séries, on obtient
![somme_(n=0)^oo\ [(n+2)(n+1) a_(n+2)+(n(n-1)+2n-2)a_n] x^n somme_(n=0)^oo\ [(n+2)(n+1) a_(n+2)+(n(n-1)+2n-2)a_n] x^n](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/fa7cf6625d240b2ee223644bdddd5e5e.png)
Prenons un exemple
F. Propriétés des séries de puissances
Égalité des séries
Si deux séries de puissances sont égales pour tous les 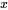 dans un intervalle ouvert contenant x_0, alors leurs coefficients doivent être égaux. Ainsi,
dans un intervalle ouvert contenant x_0, alors leurs coefficients doivent être égaux. Ainsi,
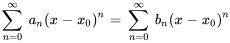
implique que 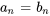 pour tous les
pour tous les 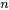 .
.
Séries de puissances disparaissant sur un intervalle
Si une série de puissances est égale à zéro pour tous les 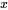 dans un intervalle ouvert, alors tous ses coefficients doivent être nuls. Ainsi,
dans un intervalle ouvert, alors tous ses coefficients doivent être nuls. Ainsi,
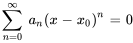
implique que 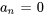 pour tous les
pour tous les 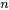 .
.
G. Séries de Taylor
Une série de Taylor est un type spécifique de représentation en série de puissances d’une fonction basée sur ses dérivées en un point spécifique, généralement en 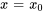 . Elle est donnée par
. Elle est donnée par
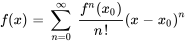
Ici, 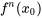 est la n-ième dérivée de
est la n-ième dérivée de 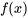 évaluée à
évaluée à 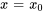 et
et 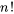 est le factoriel de
est le factoriel de 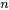 .
.
Lorsque 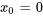 , la série est souvent appelée série de Maclaurin. Les développements de Taylor d’une nouvelle fonction en
, la série est souvent appelée série de Maclaurin. Les développements de Taylor d’une nouvelle fonction en 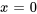 (série de Maclaurin) sont les suivants :
(série de Maclaurin) sont les suivants :
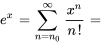
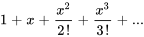
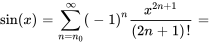
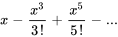
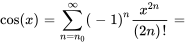
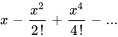
H. Relation récursive
Une relation récursive pour une série permet de calculer chaque terme de la série en utilisant un ou plusieurs des termes précédents. Au lieu de définir chaque terme indépendamment, la relation récursive relie chaque terme à ses prédécesseurs, construisant ainsi la série progressivement. Cette méthode est particulièrement utile lorsque le calcul direct des termes est complexe ou lorsque la relation entre des termes consécutifs est plus simple à exprimer.
En général, une relation récursive présente la structure suivante :
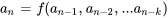 pour
pour 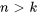
Ici, 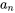 est le terme d’ordre n de la série et
est le terme d’ordre n de la série et 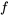 est une fonction qui définit le mode de calcul du terme d’ordre n en utilisant les termes
est une fonction qui définit le mode de calcul du terme d’ordre n en utilisant les termes 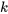 précédents.
précédents.
La relation récursive permet de calculer tous les coefficients de la série à partir d’un ensemble de conditions initiales ou de coefficients connus. Ceux-ci sont généralement dérivés des conditions initiales ou limites de l’équation différentielle.
Supposons que la formule récursive pour la solution d’une série de puissance soit
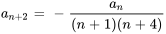
Trouver les deuxième, troisième et quatrième termes de la série en termes de 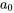 et
et 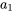 .
.
Afficher/Masquer la solution
Pour trouver les termes, il faut introduire 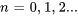 dans la relation récursive.
dans la relation récursive.
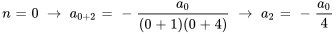
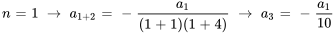
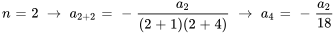
Étant donné que 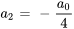 ,
, 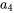 peut être écrit en termes de
peut être écrit en termes de 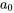 :
:
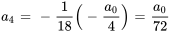
Prenons un exemple
Section 5.1 Exercices
- Écris ce qui suit sous la forme d’une série unique en termes de
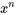 .
.
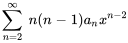
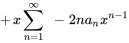
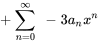
Afficher/Masquer la réponse
![somme_(n=0)^(oo)[(n+2)(n+1)a_(n+2)-2n a_n-3a_n]x^n somme_(n=0)^(oo)[(n+2)(n+1)a_(n+2)-2n a_n-3a_n]x^n](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/2af78124383a3768d20ba4c25718b5ae.png)
- Supposons
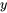 puisse être exprimé sous la forme d’une série de puissances
puisse être exprimé sous la forme d’une série de puissances 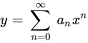 . Écris ce qui suit sous la forme d’une série unique en termes de
. Écris ce qui suit sous la forme d’une série unique en termes de 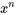 .
.
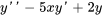
Afficher/Masquer la réponse
![somme_(n=0)^(oo)[(n+2)(n+1)a_(n+2)-5n a_n+2a_n]x^n somme_(n=0)^(oo)[(n+2)(n+1)a_(n+2)-5n a_n+2a_n]x^n](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/873f2c00e85f34e40f64b0e4b50274b2.png)
- Supposons que la formule récursive pour la solution d’une série de puissance soit
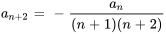
Trouvez les quatrième et cinquième termes en termes de
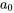 et
et 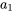 .
.Afficher/Masquer la réponse