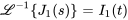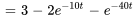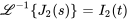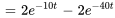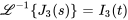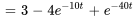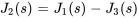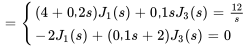4.8 Application : circuits électriques
A. Introduction
Cette section décrit brièvement l’utilisation pratique de la transformée de Laplace dans le domaine du génie électrique pour résoudre des équations différentielles et des systèmes d’équations différentielles associés à des circuits électriques. La transformée de Laplace est particulièrement utile pour convertir ces équations différentielles en formes algébriques plus faciles à gérer.
Commençons par un problème de valeur initiale (PVI) issu d’un circuit RLC de base. Nous démontrons comment la transformée de Laplace peut simplifier la recherche du courant du circuit en fonction du temps en traduisant une équation différentielle en une équation algébrique.
Prenons un circuit série RLC avec une résistance de 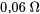 , un inducteur de
, un inducteur de 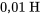 et un condensateur de
et un condensateur de 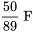 alimenté par une source de tension de
alimenté par une source de tension de 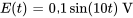 . Au départ, le courant et la charge sur le condensateur sont nuls. Déterminer le courant dans le circuit en fonction du temps.
. Au départ, le courant et la charge sur le condensateur sont nuls. Déterminer le courant dans le circuit en fonction du temps.
Afficher/Masquer la solution
Informations données :
- Résistance :
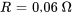
- Inducteur :
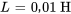
- Condensateur :
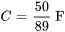
- Source de tension :
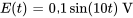
- Courant initial du condensateur :
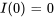
- Charge initiale du condensateur :
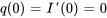
Dans l’exemple 3.9.1, nous avons développé le problème de valeur initiale régissant ce circuit RLC.
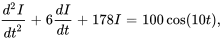
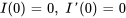
En appliquant la transformée de Laplace à l’équation différentielle, on trouve
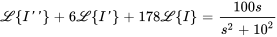
Si 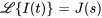 , on a
, on a
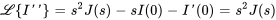
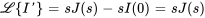
Comme 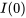 et
et 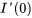 sont tous deux nuls, l’équation peut être simplifiée en
sont tous deux nuls, l’équation peut être simplifiée en
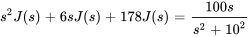
En résolvant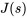 , on trouve
, on trouve
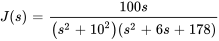
En décomposant 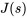 en fractions partielles, on obtient
en fractions partielles, on obtient
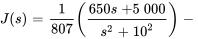
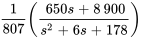
Pour simplifier la seconde fraction, il faut compléter le carré.
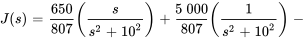
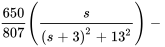
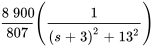
En appliquant la transformée inverse de Laplace à 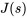 , on obtient le courant
, on obtient le courant 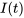 .
.
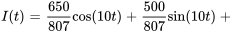
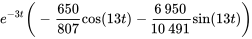
Ce résultat est conforme à celui que nous avons obtenu dans l’exemple 3.9.1 en résolvant le problème de valeur initiale au moyen de la méthode des coefficients indéterminés.
B. Résolution de systèmes d’équations linéaires avec la transformée de Laplace
La transformée de Laplace peut être appliquée pour transformer certains systèmes d’équations différentielles avec valeurs initiales en systèmes d’équations algébriques dans le domaine s. La résolution de ces équations algébriques permet de trouver des fonctions de 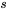 , que l’on peut ensuite reconvertir en solutions dans le domaine temporel à l’aide de la transformée inverse de Laplace. Nous aborderons ensuite un exemple plus complexe impliquant un circuit série-parallèle RL, qui se traduit par un système d’équations différentielles.
, que l’on peut ensuite reconvertir en solutions dans le domaine temporel à l’aide de la transformée inverse de Laplace. Nous aborderons ensuite un exemple plus complexe impliquant un circuit série-parallèle RL, qui se traduit par un système d’équations différentielles.
a) Pour le schéma de circuit électrique donné, déterminer le système d’équations différentielles qui décrit les courants dans les différentes branches du circuit. Supposons que tous les courants initiaux sont nuls. b) Une fois que le système d’équations différentielles et les conditions initiales sont établis, résoudre le système pour les courants dans chaque branche du circuit.
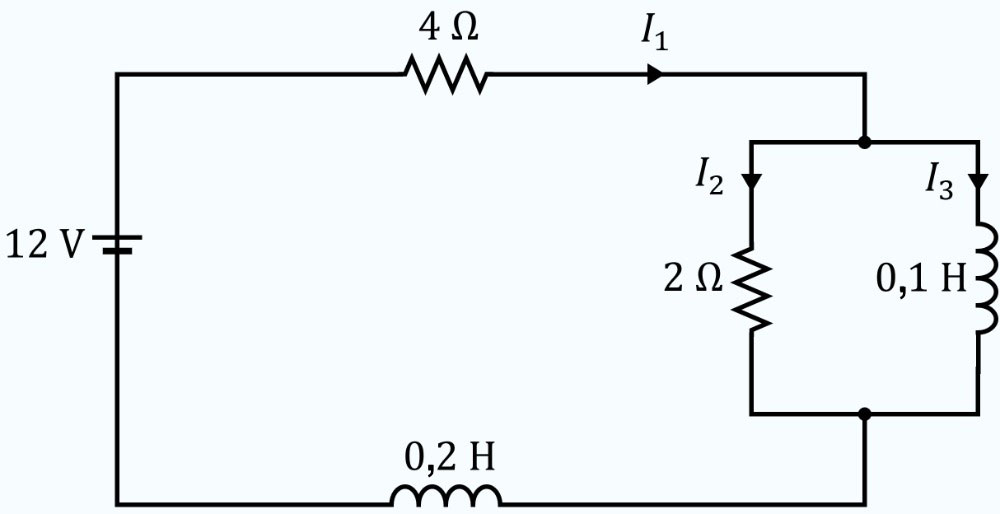
Description du schéma
Afficher/Masquer la solution
On représente le courant passant par la branche principale par 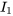 , le courant passant par la résistance de 2 Ω par
, le courant passant par la résistance de 2 Ω par 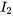 et le courant passant par l’inducteur de 0,1 H par
et le courant passant par l’inducteur de 0,1 H par 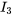 .
.
Étant donné que la baisse de tension aux bornes d’une résistance est 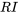 et, aux bornes d’un inducteur,
et, aux bornes d’un inducteur, 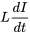 , on applique la loi des mailles de Kirchhoff au réseau électrique.
, on applique la loi des mailles de Kirchhoff au réseau électrique.
Dans la boucle principale comprenant un inducteur de 0,1 H, on trouve
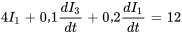
Dans la sous-branche comprenant la résistance de 2 Ω et l’inducteur de 0,1 H, on trouve
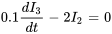
De même, comme le courant 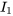 est divisé en
est divisé en 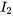 et
et 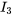 , on a
, on a
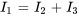
Le système d’équations décrivant les courants dans le circuit est donc
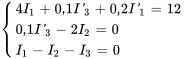
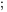
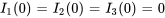 (4.8.1)
(4.8.1)
b)
Pour résoudre le système, il faut appliquer la transformée de Laplace à chacune des équations du système :
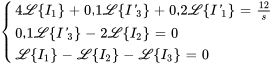 (4.8.2)
(4.8.2)
Si 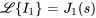 ,
, 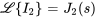 et
et 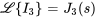 , on a
, on a
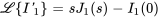
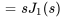
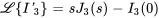
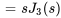
Comme les courants initiaux sont nuls, le système présenté à la section 4.8.2 peut être simplifié en
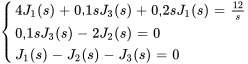
Dans la troisième équation, on exprime 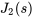 en fonction des deux autres variables.
en fonction des deux autres variables.
Ensuite, on remplace cette expression par 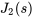 dans la deuxième équation, ce qui réduit le système à deux équations à deux inconnues.
dans la deuxième équation, ce qui réduit le système à deux équations à deux inconnues.
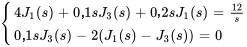
Pour éliminer 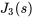 , on multiplie la première équation par
, on multiplie la première équation par 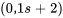 et la deuxième équation par
et la deuxième équation par 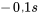 , à la suite de quoi on additionne les deux équations. Cela donne
, à la suite de quoi on additionne les deux équations. Cela donne
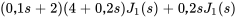
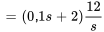
En réarrangeant 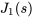 , on obtient
, on obtient
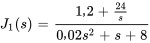
Pour éliminer les termes décimaux et rationnels, on multiplie le numérateur et le dénominateur par 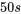 .
.
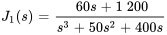
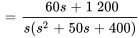
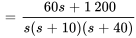
En décomposant 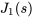 en fractions partielles, on obtient
en fractions partielles, on obtient
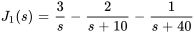
En remplaçant 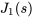 dans la deuxième équation du système 4.8.4, on trouve
dans la deuxième équation du système 4.8.4, on trouve 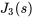 .
.
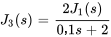
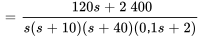
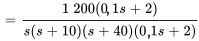
Ce qui peut être simplifié en
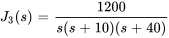
En décomposant 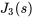 en fractions partielles, on obtient
en fractions partielles, on obtient
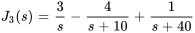
En remplaçant les expressions pour 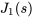 et
et 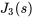 dans l’équation 4.8.3, on trouve
dans l’équation 4.8.3, on trouve 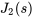 .
.
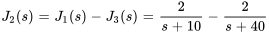
Enfin, en appliquant la transformée inverse de Laplace à 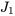 ,
, 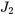 , et
, et 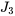 , on détermine le courant dans les branches du circuit.
, on détermine le courant dans les branches du circuit.