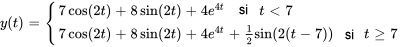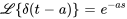4.7 Fonction delta de Dirac (impulsion)
Dans les sections précédentes, nous avons exploré des problèmes de valeur initiale pour des équations différentielles du second ordre à coefficients constants, en nous concentrant sur les cas où la fonction de forçage,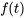 
, est soit continue, soit continue par morceaux sur l’intervalle 
.
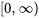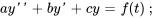
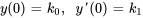
Intéressons-nous maintenant à un autre type de fonction de forçage : celle qui représente une force d’impulsion. Les forces d’impulsion se caractérisent par des amplitudes très importantes sur des intervalles de temps extrêmement courts, à la façon d’une brusque « secousse » ou d’un « pic » soudain dans le système. De telles impulsions se produisent dans divers contextes, notamment dans les circuits électriques lors de l’activation, dans les systèmes mécaniques lors d’une collision ou dans tout scénario où une force soudaine et importante est appliquée pendant une brève période.
A. Fonction delta de Dirac
Pour modéliser mathématiquement ces forces d’impulsion, on utilise la fonction delta de Dirac, à savoir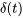 
. La fonction delta de Dirac n’est pas une fonction au sens traditionnel du terme, mais plutôt une fonction généralisée ou une distribution dotée des propriétés suivantes.
1. Nulle partout sauf en 0 :
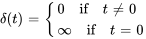
2. Intégrale égale à 1 :
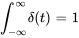
3. Propriété de criblage :
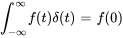pour toute fonction 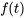qui est continue sur l’intervalle contenant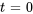 
En déplaçant l’argument 
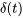dans , il est possible de modéliser les impulsions qui se produisent à des instants autres que 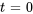. La fonction delta de Dirac déplacée, 
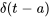, marque un pic à 
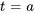et est définie comme suit :
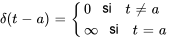
La propriété de criblage s’étend donc à
4. Criblage en :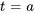
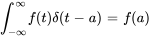pour toute fonction 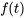qui est continue sur l’intervalle contenant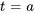
B. Transformée de Laplace de la fonction delta de Dirac
La transformée de Laplace offre une moyen pratique traiter la fonction Delta de Dirac dans le cadre de la résolution d’équations différentielles. La transformée d’une fonction delta de Dirac déplacée est donnée par
Il importe de comprendre la fonction Delta de Dirac et ses propriétés pour modéliser et analyser des systèmes soumis à des forces d’impulsion.
Trouver la solution du problème de valeur initiale
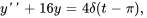
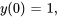
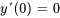
Afficher/Masquer la solution
En prenant la transformée de Laplace de l’équation et en appliquant l’équation de la section 4.7.1 avec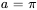 
à la fonction delta, on obtient
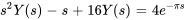
La résolution pour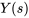 
donne
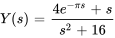
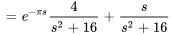
En calculant la transformée inverse de Laplace, on obtient
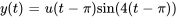
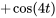
Ce qui est équivalent à
La figure ci-dessous montre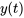 
. La force d’impulsion est appliquée et ajoute de l’élan au système en 
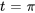. Pour comparaison, la ligne en pointillés représente le système non perturbé.
Prenons un exemple
Section 4.7 Exercices
- Résous le problème de valeur initiale
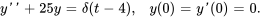
Afficher/Masquer la réponse
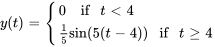
- Résous le problème de valeur initiale
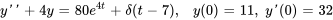
Afficher/Masquer la réponse
