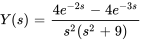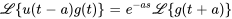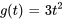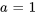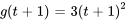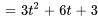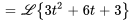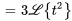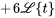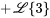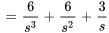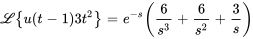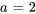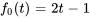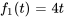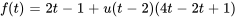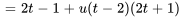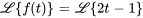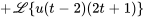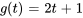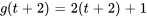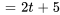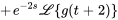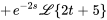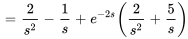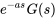4.5 Transformée de Laplace de fonctions définies par morceaux
A. Fonction en escalier
Dans cette section, nous explorons l’application des transformées de Laplace à des fonctions continues par morceaux. Dans la section suivante, nous tâcherons de résoudre des problèmes de valeur initiale impliquant des équations différentielles du second ordre à coefficients constants où la fonction de forçage 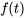 est une fonction continue par morceaux.
est une fonction continue par morceaux.
Les discontinuités à saut fini se produisent souvent dans des situations physiques telles que des mécanismes de commutation ou des changements brusques de forces agissant sur le système. Pour traiter ces discontinuités dans le domaine de Laplace, nous utilisons la fonction échelon unité pour transformer des fonctions définies par morceaux en une forme adaptée aux transformées de Laplace et trouver ensuite des inverses continues par morceaux des transformées de Laplace pour la solution.
La fonction échelon unité (ou fonction de Heaviside) 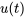 est définie comme suit :
est définie comme suit :
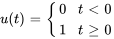
Elle passe de 0 à 1 par échelons (ou sauts) à 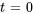 . En déplaçant l’argument
. En déplaçant l’argument  , on peut déplacer l’échelon à différents endroits.
, on peut déplacer l’échelon à différents endroits.
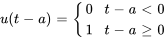

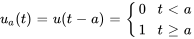
La fonction en escalier peut également être transformée, par exemple déplacée, étendue ou comprimée. Par exemple, en multipliant 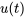 par une constante
par une constante  , on peut l’étendre verticalement.
, on peut l’étendre verticalement.

Ou en combinant le déplacement et la réflexion de 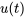 , on peut opposer la permutation de la fonction.
, on peut opposer la permutation de la fonction.
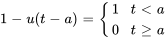
La fonction en escalier permet de représenter aisément n’importe quelle fonction continue par morceaux. Par exemple, prenons la fonction
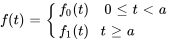
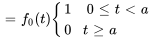
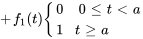
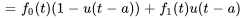
Elle peut être réécrite sous la forme
On peut étendre l’équation de la section 4.5.1 à des fonctions continues par morceaux plus générales.
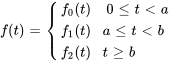
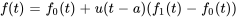
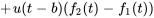 (4.5.2)
(4.5.2)
B. Transformée de Laplace de fonctions définies par morceaux
La transformée de Laplace de la fonction modulée par échelons est essentielle pour résoudre les équations différentielles avec des fonctions de forçage définies par morceaux.
Théorème : transformée de Laplace d’une fonction modulée par échelons. Soit  défini sur
défini sur 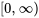 et
et 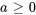 , supposons que
, supposons que 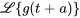 existe pour
existe pour  . Alors,
. Alors,
Ce théorème permet la transformation de fonctions modulées par échelons dans le domaine de Laplace, qui peut alors être manipulé algébriquement.
Trouver la transformée de Laplace de  .
.
Trouver la transformée de Laplace de
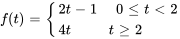
Prenons un exemple
C. Transformée inverse de Laplace de fonctions définies par morceaux
Le théorème précédent permet également de déterminer la transformée inverse de Laplace des fonctions issues de fonctions définies par morceaux. Cependant, il sera plus pratique de déplacer l’argument de  et de remplacer
et de remplacer  avec
avec 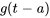 .
.
Théorème de translation en  . Si
. Si  et si
et si  existe pour
existe pour  , alors
, alors
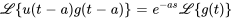
Étant donné que 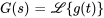 , c’est équivalent à
, c’est équivalent à
Trouver la transformée inverse de Laplace de la fonction donnée et trouver des formules distinctes pour 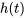 aux intervalles appropriés.
aux intervalles appropriés.
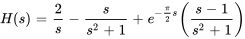
Afficher/Masquer la solution
Comme 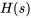 a
a 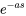 comme facteur, il faut utiliser l’équation 4.5.4 pour déterminer l’inverse.
comme facteur, il faut utiliser l’équation 4.5.4 pour déterminer l’inverse.
Avec 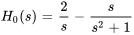 et
et 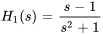 , on obtient
, on obtient
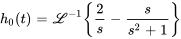
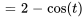
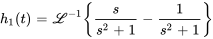
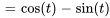
En utilisant l’équation 4.5.4 avec  et une linéarité de
et une linéarité de  , on a
, on a
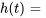
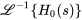
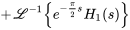
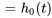
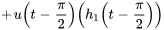
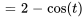
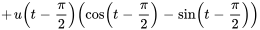
On peut simplifier en utilisant des identités trigonométriques : 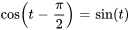 et
et  . L’application de ces identités donne
. L’application de ces identités donne
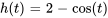
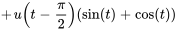
Grâce à l’équation 4.5.1, on sait que
- L’expression sans fonction unité,
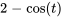 , correspond à
, correspond à  , la fonction active avant l’échelon.
, la fonction active avant l’échelon. - L’expression multipliée par la fonction unité,
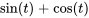 , représente le changement dans la fonction à l’échelon, correspondant donc à
, représente le changement dans la fonction à l’échelon, correspondant donc à  .
.
Étant donné que 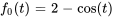 , il est possible de trouver la valeur de
, il est possible de trouver la valeur de 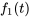 .
.
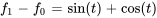

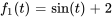
On peut maintenant exprimer 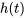 comme une fonction définie par morceaux.
comme une fonction définie par morceaux.
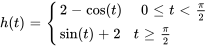
Prenons un exemple
Section 4.5 Exercices
- Trouve la transformée de Laplace,
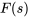 , de
, de 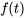 .
.

Afficher/Masquer la réponse
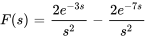
- Prends la transformée inverse de Laplace pour déterminer
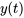 . Entre
. Entre 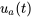 pour
pour 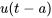 si la fonction unité est une partie de l’inverse.
si la fonction unité est une partie de l’inverse.
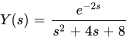
Afficher/Masquer la réponse
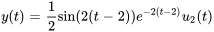
- Applique la transformée de Laplace à l’équation différentielle et trouve la valeur de
 .
.
Afficher/Masquer la réponse