4.3 Transformée inverse de Laplace
Dans les sections précédentes, nous avons défini la transformée de Laplace comme un opérateur intégral capable de représenter une fonction 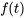 et ses dérivées dans une équation différentielle en une équation algébrique en termes de
et ses dérivées dans une équation différentielle en une équation algébrique en termes de 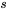 et de fonction
et de fonction 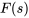 . Pour résoudre des équations différentielles, il faut souvent obtenir
. Pour résoudre des équations différentielles, il faut souvent obtenir 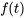 à partir de sa transformée
à partir de sa transformée 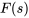 afin de résoudre le problème de valeur initiale d’origine. Ce processus est facilité par la transformée inverse de Laplace.
afin de résoudre le problème de valeur initiale d’origine. Ce processus est facilité par la transformée inverse de Laplace.
En règle générale, la formule d’inversion formelle n’est pas directement utilisée en raison de sa complexité. Au lieu de cela, on fait appel aux tables de transformées de Laplace pour trouver les transformées inverses de 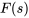 obtenues à partir du problème d’origine. La transformée inverse de Laplace est représentée par
obtenues à partir du problème d’origine. La transformée inverse de Laplace est représentée par
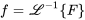
Linéarité de la transformée inverse de Laplace
Tout comme la transformée de Laplace, l’opération inverse est linéaire. Si 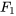 et
et 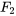 sont des fonctions dans le domaine s avec des constantes
sont des fonctions dans le domaine s avec des constantes 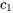 et
et 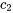 , de sorte que la transformée inverse de Laplace d’une combinaison linéaire de
, de sorte que la transformée inverse de Laplace d’une combinaison linéaire de 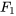 et
et 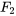 pour
pour  est donnée par
est donnée par
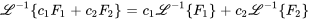
Cette propriété garantit que le processus de recherche de la transformée inverse d’une expression compliquée peut souvent être décomposé en parties plus simples et plus faciles à gérer.
Déterminer 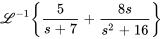 .
.
Afficher/Masquer la solution
À partir de la table 4.1
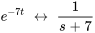 et
et 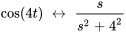
À partir de la linéarité, on obtient donc
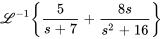
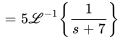
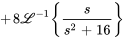
À partir de la table des transformées de Laplace, on obtient
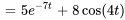
Prenons un exemple
Prenons un exemple
Dans le processus de recherche de la transformée de Laplace inverse, on rencontre souvent la fonction rationnelle 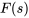 sous la forme
sous la forme
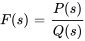
Ici, 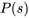 et
et 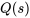 sont des polynômes. Pour s’assurer que
sont des polynômes. Pour s’assurer que 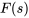 représente une transformée de Laplace valide, on considère généralement des cas où le degré de
représente une transformée de Laplace valide, on considère généralement des cas où le degré de 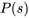 est inférieur à celui de
est inférieur à celui de 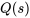 , car on peut montrer que
, car on peut montrer que 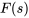 est une transformée de Laplace si
est une transformée de Laplace si 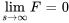 . Cette condition est souvent appelée condition de régularité d’une fonction rationnelle dans le domaine de Laplace.
. Cette condition est souvent appelée condition de régularité d’une fonction rationnelle dans le domaine de Laplace.
Dans ce cas, la recherche de l’inverse peut nécessiter de compléter le carré du dénominateur ou d’effectuer un développement partiel de la fraction, une technique similaire à celle utilisée dans le calcul intégral. Ces techniques sont particulièrement nécessaires lorsque l’on tente de faire correspondre 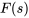 à une transformée inversée connue à partir de tables standard. Le choix entre la complétion du carré et la décomposition en fractions partielles dépend de la nature et de la composition du dénominateur
à une transformée inversée connue à partir de tables standard. Le choix entre la complétion du carré et la décomposition en fractions partielles dépend de la nature et de la composition du dénominateur 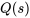 .
.
- La décomposition en fractions partielles constitue souvent la première approche considérée. Elle est efficace lorsque le dénominateur
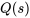 est factorisable en facteurs linéaires ou quadratiques irréductibles. Cette technique décompose les expressions rationnelles complexes en parties plus simples, ce qui facilite la recherche de la transformée inverse de Laplace pour chaque terme individuel.
est factorisable en facteurs linéaires ou quadratiques irréductibles. Cette technique décompose les expressions rationnelles complexes en parties plus simples, ce qui facilite la recherche de la transformée inverse de Laplace pour chaque terme individuel. - La complétion du carré est utilisée lorsque le dénominateur
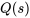 comporte des termes quadratiques qui ne se factorisent pas en termes linéaires réels, ce qui indique souvent des racines complexes.
comporte des termes quadratiques qui ne se factorisent pas en termes linéaires réels, ce qui indique souvent des racines complexes.
Pour illustrer ces méthodes, voici quelques exemples montrant comment appliquer ces techniques pour trouver la transformée inverse de Laplace de diverses fonctions.
Trouver la transformée inverse de Laplace
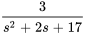
Afficher/Masquer la solution
Le dénominateur n’est pas factorisable. On doit donc essayer de compléter le carré :
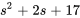
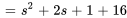
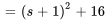
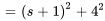
À partir de la table 4.1, on voit que
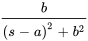
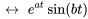
Ainsi, 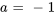 et
et 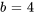 . Pour pouvoir utiliser la transformée inverse ci-dessus, il faut créer un 4 dans le numérateur. On multiplie donc le numérateur et le dénominateur de la fonction d’origine par 4. On obtient
. Pour pouvoir utiliser la transformée inverse ci-dessus, il faut créer un 4 dans le numérateur. On multiplie donc le numérateur et le dénominateur de la fonction d’origine par 4. On obtient
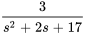
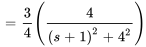
On peut maintenant utiliser l’inverse de la table
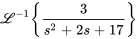
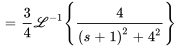
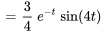
Prenons un exemple
Trouver la transformée inverse de Laplace
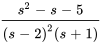
Afficher/Masquer la solution
Dans le dénominateur, on a un facteur linéaire répété  de multiplicité deux et un facteur linéaire non répété
de multiplicité deux et un facteur linéaire non répété  . Cette composition nous conduit à structurer la décomposition en fractions partielles comme suit :
. Cette composition nous conduit à structurer la décomposition en fractions partielles comme suit :
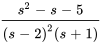
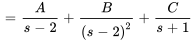
Une façon de trouver les constantes A, B et C consiste à multiplier les deux côtés de l’égalité par 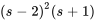 afin d’éliminer les dénominateurs :
afin d’éliminer les dénominateurs :
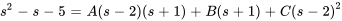
On peut alors trouver la valeur des constantes en mettant en équation les coefficients de termes similaires des deux côtés. Cela forme un système d’équations.
Une autre méthode, souvent plus simple, consiste à choisir stratégiquement des valeurs pour 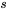 qui simplifient l’équation et isolent chacune des constantes. Par exemple :
qui simplifient l’équation et isolent chacune des constantes. Par exemple :
Pour B : soit 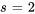 , ce qui annule les termes avec A et C et conduit à :
, ce qui annule les termes avec A et C et conduit à :
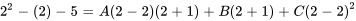
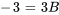

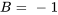
Pour C : soit 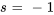 , ce qui simplifie l’équation pour trouver la valeur de C :
, ce qui simplifie l’équation pour trouver la valeur de C :
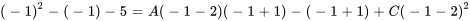
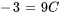

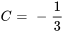
Pour A : choisir un 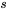 différent, par exemple
différent, par exemple 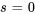 , pour isoler et trouver la valeur de A :
, pour isoler et trouver la valeur de A :
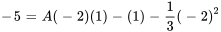

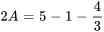

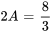
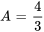
Avec 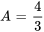 ,
, 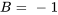 , et
, et 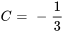 , la fraction partielle devient
, la fraction partielle devient
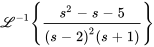
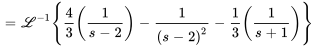
Avec la linéarité, la transformée inverse de Laplace est
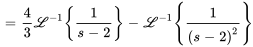
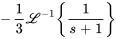
Et, en se référant à la table des transformées inversés, on a
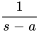
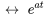 et
et 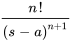
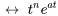
En appliquant cela avec 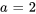 pour les deux premiers termes et
pour les deux premiers termes et 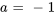 pour le dernier terme, on obtient
pour le dernier terme, on obtient
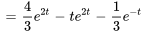
Prenons un exemple
Section 4.3 Exercices
-
- Trouve la transformée inverse de Laplace de la fonction
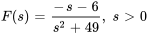 .
.
Afficher/Masquer la réponse
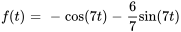
- Trouve la transformée inverse de Laplace de
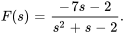
Afficher/Masquer la réponse
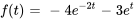
- En résolvant une équation différentielle avec la transformée de Laplace,
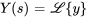 est
est
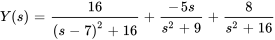
Trouve la transformée inverse de Laplace de
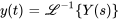 .
.Afficher/Masquer la réponse
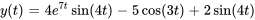
- Trouve la transformée inverse de Laplace de la fonction
