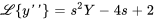4.2 Propriétés de la transformée de Laplace
Il est essentiel de comprendre les propriétés de la transformée de Laplace, car elle fournit des outils permettant de transformer et de manipuler efficacement les fonctions. Ces propriétés simplifient grandement l’analyse et la résolution des équations différentielles et des systèmes complexes.
A. Existence de la transformée
La transformée de Laplace existe pour toute fonction qui est (1) continue par morceaux et (2) d’ordre exponentiel (c’est-à-dire qui ne croît pas plus vite qu’une fonction exponentielle). Une fonction 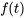 est dite d’ordre exponentiel
est dite d’ordre exponentiel 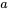 s’il existe des constantes positives
s’il existe des constantes positives 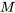 et si
et si 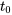 , de sorte que
, de sorte que 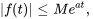 pour tous les
pour tous les 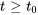 . Par exemple,
. Par exemple, 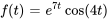 est d’ordre exponentiel 7, mais
est d’ordre exponentiel 7, mais 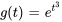 n’est pas d’ordre exponentiel.
n’est pas d’ordre exponentiel.
B. Linéarité de la transformée de Laplace
La transformée de Laplace obéit au principe de linéarité. Disons que 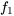 et
et 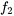 sont des fonctions pour lesquelles existe la transformée de Laplace
sont des fonctions pour lesquelles existe la transformée de Laplace  et que
et que 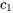 et
et 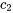 sont des constantes. Alors, pour
sont des constantes. Alors, pour  , la transformée de Laplace d’une combinaison linéaire de ces fonctions est donnée par :
, la transformée de Laplace d’une combinaison linéaire de ces fonctions est donnée par :
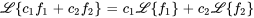
Cette propriété est utile avec les combinaisons linéaires de fonctions.
Utiliser la table des transformées de Laplace et la propriété de linéarité pour déterminer
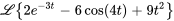 .
.
Afficher/Masquer la solution
1. À partir de la table
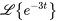
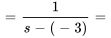
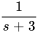 pour
pour 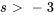
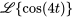
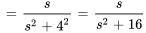 pour
pour 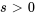
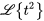
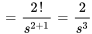 pour
pour 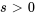
2. À partir du théorème de linéarité, on a
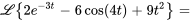
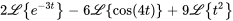
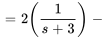
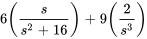
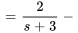
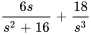 pour
pour 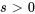
Prenons un exemple
C. Premier théorème du déplacement
Si 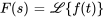 , alors
, alors
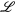
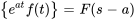
Ce théorème est très utile pour résoudre des équations différentielles avec des termes exponentiels ou pour analyser des systèmes avec des entrées exponentielles.
Utiliser le premier théorème du déplacement et la propriété de linéarité pour déterminer
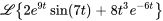 .
.
Afficher/Masquer la solution
Avec le premier théorème du déplacement, on a
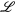
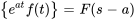
1. Dans 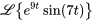 ,
, 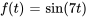 et le coefficient dans l’exposant du terme exponentiel est
et le coefficient dans l’exposant du terme exponentiel est 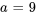 .
.
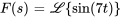
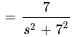 pour
pour 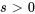
En déplaçant 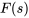 , on remplace
, on remplace 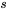 par
par 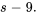
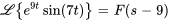
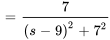 pour
pour 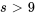
2. Dans 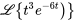 ,
, 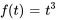 et le coefficient dans l’exposant du terme exponentiel est
et le coefficient dans l’exposant du terme exponentiel est 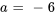 .
.
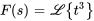
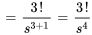 pour
pour 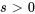
En déplaçant 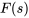 , on remplace
, on remplace 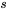 par
par 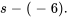
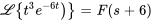
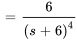 pour
pour 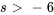
3. À partir du théorème de linéarité, on a
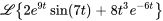
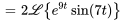

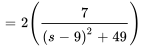
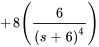
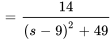
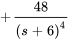 pour
pour 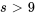
Prenons un exemple
D. Différenciation dans le domaine temporel
Il faut absolument savoir transformer les dérivées pour résoudre efficacement des équations différentielles. Cette propriété permet d’exprimer la transformée de Laplace de la dérivée d’une fonction en termes de transformée de la fonction originale. Pour une fonction 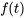 avec des dérivées continues jusqu’au
avec des dérivées continues jusqu’au 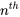 ordre,
ordre,
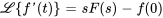
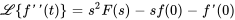
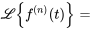
Comme nous traiterons principalement d’équations différentielles du second ordre, nous nous concentrerons sur la transformée de Laplace des dérivées première et seconde.
Pour la fonction 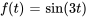 , montrer que
, montrer que 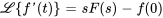 .
.
Afficher/Masquer la solution
Identifier la dérivée et la valeur initiale :
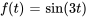

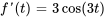 et
et
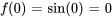
Trouver les transformées de Laplace :
À partir de la table des transformées de Laplace, on a
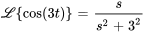
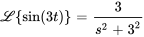
Appliquer la propriété de différenciation :
Il faut montrer
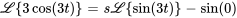
En introduisant les transformées et la valeur initiale, on obtient
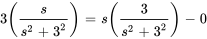
Et, en simplifiant les deux côtés, on a
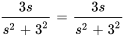
Cette égalité confirme la propriété de différenciation, puisque les deux côtés sont identiques.
Trouver la transformée de Laplace de 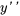 étant donné les conditions initiales
étant donné les conditions initiales 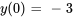 et
et 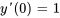 . Utiliser
. Utiliser 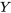 pour
pour 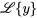 .
.
Afficher/Masquer la solution
À partir de la propriété de différenciation, on a
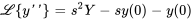
En insérant les conditions initiales 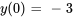 et
et 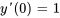 , on obtient
, on obtient
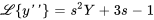
Prenons un exemple
La table 4.2.1 résume les propriétés ci-dessus de la transformée de Laplace. Ces propriétés sont cruciales pour simplifier les calculs et utiliser efficacement la transformée de Laplace dans la résolution des problèmes de valeur initiale.
Table 4.2.1 : Propriétés de la transformée de Laplace
| Propriété | Exemple |
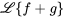 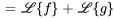 |
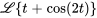 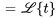 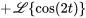 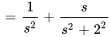 |
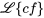 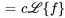 pour n’importe quelle constante pour n’importe quelle constante  |
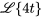 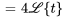 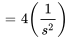 |
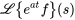 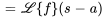 |
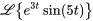 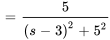 |
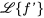 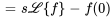 |
|
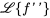 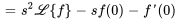 |
|
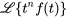 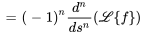 |
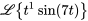 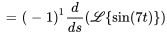 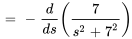 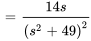 |
Section 4.2 Exercices
- Trouve la transformée de Laplace de la fonction
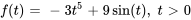 .
.
Afficher/Masquer la réponse
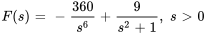
- Trouve la transformée de Laplace,
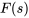 , de la fonction
, de la fonction
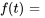
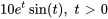 .
.Afficher/Masquer la réponse
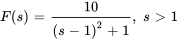
- Trouve la transformée de Laplace de
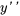 compte tenu des conditions initiales
compte tenu des conditions initiales 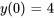 et
et 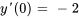 .
.
Afficher/Masquer la réponse