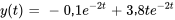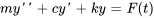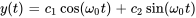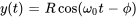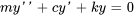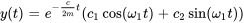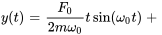3.8 Application : vibrations mécaniques
A. Introduction
En passant ainsi des équations différentielles ordinaires du premier ordre à celles du second ordre, nous allons découvrir diverses applications qui peuvent être modélisées par ces équations d’ordre supérieur. Dans cette section et les suivantes, nous abordons deux grands domaines où les équations différentielles du second ordre sont largement appliquées : les vibrations mécaniques et les circuits électriques (circuits RLC). Fondamentaux en ingénierie et en physique, ces domaines fournissent de précieux contextes pour comprendre le comportement des systèmes dynamiques.
L’étude des vibrations mécaniques est cruciale pour la conception et l’analyse des systèmes qui subissent des mouvements oscillatoires. La compréhension des vibrations aide les ingénieurs à réduire le bruit, à prévenir les défaillances catastrophiques dues à la résonance et à optimiser les performances de divers systèmes mécaniques, allant des bâtiments et des ponts aux suspensions de véhicules et aux composants électroniques. La modélisation de ces systèmes permet aux ingénieurs de prévoir les réponses à divers stimuli, garantissant ainsi la sécurité et la fonctionnalité.
Pour modéliser un système vibratoire, nous nous servons généralement d’une représentation simplifiée impliquant des masses, des ressorts et des amortisseurs. Ces éléments illustrent la dynamique essentielle de systèmes réels plus complexes. En utilisant les lois du mouvement de Newton ou des méthodes énergétiques, nous développons un modèle mathématique qui se traduit généralement par une équation différentielle du second ordre.
B. Composants d’un système ressort-masse
Le système consiste en une masse, typiquement désignée par 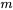 , qui représente l’objet en mouvement. Un ressort au coefficient de rigidité
, qui représente l’objet en mouvement. Un ressort au coefficient de rigidité 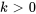 lui est attaché, produisant une force de rappel proportionnelle et opposée au déplacement par rapport à sa position d’équilibre, conformément à la loi de Hooke. Dans de nombreux scénarios pratiques, ce système peut également être doté d’un composant amortisseur caractérisé par un coefficient d’amortissement
lui est attaché, produisant une force de rappel proportionnelle et opposée au déplacement par rapport à sa position d’équilibre, conformément à la loi de Hooke. Dans de nombreux scénarios pratiques, ce système peut également être doté d’un composant amortisseur caractérisé par un coefficient d’amortissement , représentant la résistance au mouvement due à des facteurs tels que la résistance de l’air ou le frottement interne dans le système. L’amortisseur exerce une force qui est proportionnelle à la vitesse de la masse, mais dans la direction opposée au mouvement. En outre, le système peut être soumis à une force externe
, représentant la résistance au mouvement due à des facteurs tels que la résistance de l’air ou le frottement interne dans le système. L’amortisseur exerce une force qui est proportionnelle à la vitesse de la masse, mais dans la direction opposée au mouvement. En outre, le système peut être soumis à une force externe 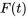 , qui peut varier dans le temps et induire des vibrations forcées.
, qui peut varier dans le temps et induire des vibrations forcées.
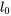 lorsqu’il n’est pas étiré. Lorsqu’on attache une masse
lorsqu’il n’est pas étiré. Lorsqu’on attache une masse 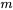 au ressort, celui-ci s’étire d’une longueur
au ressort, celui-ci s’étire d’une longueur  . Le point où la masse s’immobilise et où le ressort cesse de s’étirer est la position d’équilibre. À ce point, le système est stable et la masse reste immobile tant que rien ne vient la perturber. Dans ce système, nous définissons
. Le point où la masse s’immobilise et où le ressort cesse de s’étirer est la position d’équilibre. À ce point, le système est stable et la masse reste immobile tant que rien ne vient la perturber. Dans ce système, nous définissons  comme le déplacement de la masse par rapport à sa position d’équilibre, où les valeurs positives indiquent un mouvement vers le haut.
comme le déplacement de la masse par rapport à sa position d’équilibre, où les valeurs positives indiquent un mouvement vers le haut.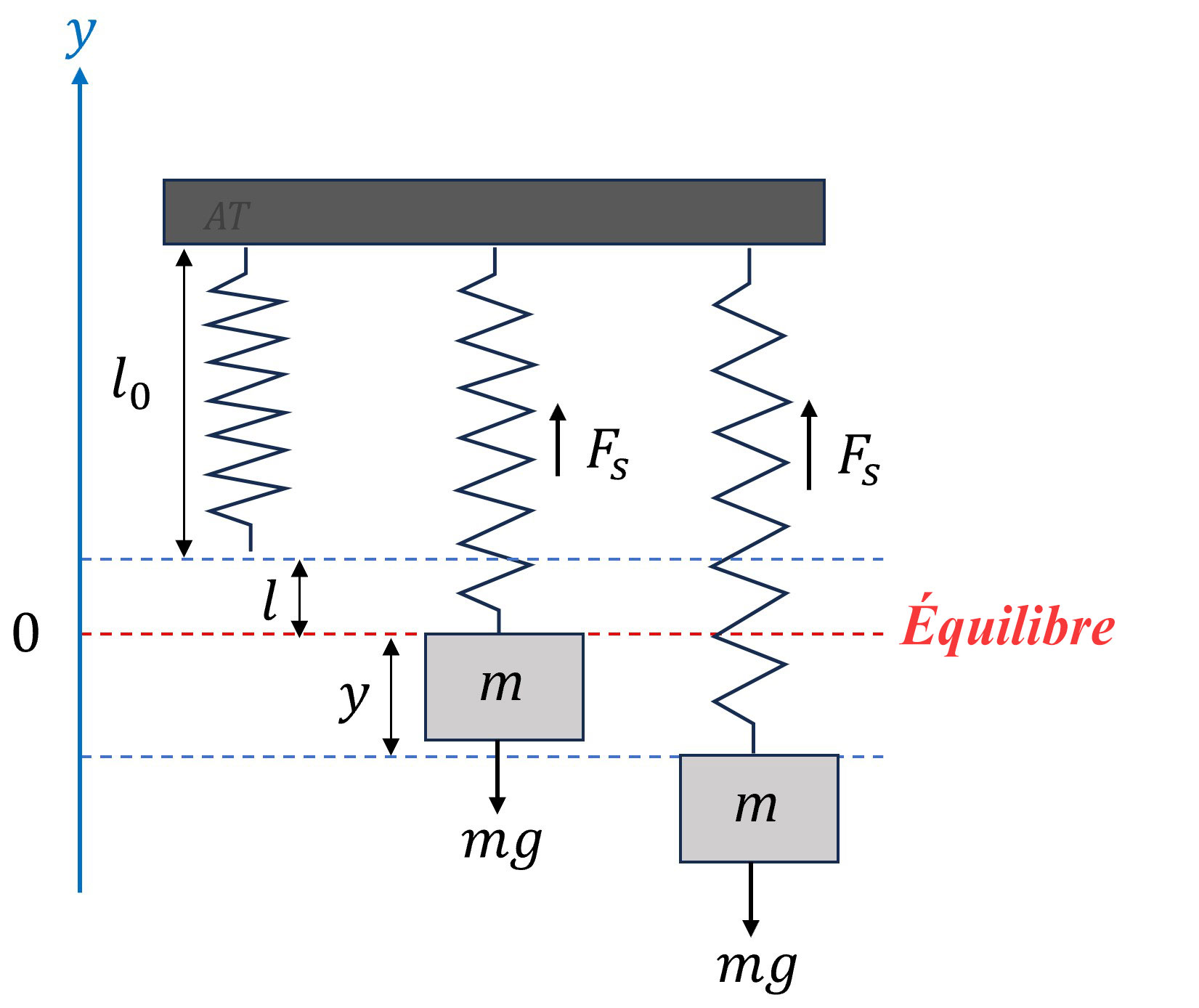
C. Équation différentielle générale de modélisation du système
Pour dériver l’équation régissant le mouvement d’un système ressort-masse-amortisseur, nous appliquons la deuxième loi du mouvement de Newton, qui établit la force nette agissant sur la masse et son accélération. Les principales forces agissant sur la masse dans un système ressort-masse sont les suivantes :
- Force due à la pesanteur
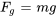 agissant vers le bas.
agissant vers le bas. - Force de rappel du ressort
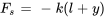 , où
, où  est la constante du ressort. Cette force est définie par la loi de Hooke et est généralement proportionnelle au déplacement par rapport à la longueur naturelle du ressort (
est la constante du ressort. Cette force est définie par la loi de Hooke et est généralement proportionnelle au déplacement par rapport à la longueur naturelle du ressort (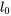 ) et de direction opposée.
) et de direction opposée. - Force d’amortissement
 , où
, où  est le coefficient d’amortissement. Si elle est présente, la force d’amortissement est proportionnelle à la vitesse de la masse, mais dans la direction opposée au mouvement.
est le coefficient d’amortissement. Si elle est présente, la force d’amortissement est proportionnelle à la vitesse de la masse, mais dans la direction opposée au mouvement. - Force externe
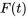 . Il s’agit de toute force agissant sur le système, qui peut être périodique ou aléatoire, et induisant des vibrations forcées.
. Il s’agit de toute force agissant sur le système, qui peut être périodique ou aléatoire, et induisant des vibrations forcées.
D’après la deuxième loi du mouvement de Newton,
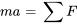
En substituant toutes les forces et en écrivant l’accélération comme la dérivée seconde du déplacement, on obtient

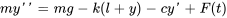
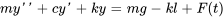
Au point d’équilibre, la somme de toutes les forces agissant sur la masse est égale à zéro. Par conséquent,

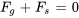
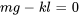
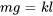
Si l’on simplifie l’équation en introduisant 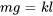 pour se concentrer sur les écarts par rapport à l’équilibre, on obtient la forme standard de l’équation de vibration.
pour se concentrer sur les écarts par rapport à l’équilibre, on obtient la forme standard de l’équation de vibration.
Ici, 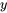 est le déplacement par rapport à la position d’équilibre,
est le déplacement par rapport à la position d’équilibre, 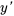 est la vitesse,
est la vitesse, 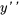 est l’accélération et
est l’accélération et 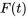 représente toute force externe appliquée sur le système. On résout généralement cette équation avec les conditions initiales pour le déplacement initial de la position d’équilibre :
représente toute force externe appliquée sur le système. On résout généralement cette équation avec les conditions initiales pour le déplacement initial de la position d’équilibre : 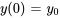 et la vitesse initiale :
et la vitesse initiale : 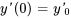 .
.
Selon les forces qui agissent sur le système, il existe plusieurs cas particuliers :
- Vibration libre non amortie (
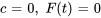 ) : la forme la plus simple de vibration se produit lorsqu’il n’y a ni amortissement, ni force externe. Le système oscille à sa fréquence naturelle, déterminée par la masse et la constante du ressort.
) : la forme la plus simple de vibration se produit lorsqu’il n’y a ni amortissement, ni force externe. Le système oscille à sa fréquence naturelle, déterminée par la masse et la constante du ressort. - Vibration libre amortie (
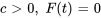 ) : lorsque l’amortissement est présent mais qu’il n’y a pas de force extérieure, le système subit des vibrations amorties qui entraînent une diminution progressive de l’amplitude de l’oscillation au fil du temps. La nature de l’amortissement (sous-amortissement, amortissement critique, sur-amortissement) dépend des valeurs de
) : lorsque l’amortissement est présent mais qu’il n’y a pas de force extérieure, le système subit des vibrations amorties qui entraînent une diminution progressive de l’amplitude de l’oscillation au fil du temps. La nature de l’amortissement (sous-amortissement, amortissement critique, sur-amortissement) dépend des valeurs de 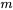 ,
,  et
et  .
. - Vibration forcée non amortie (
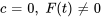 ) : lorsqu’une force externe agit sur le système, celui-ci subit des vibrations forcées. Si la fréquence de la force externe est proche de la fréquence naturelle du système, il peut y avoir de la résonance,entraînant des oscillations de grande amplitude.
) : lorsqu’une force externe agit sur le système, celui-ci subit des vibrations forcées. Si la fréquence de la force externe est proche de la fréquence naturelle du système, il peut y avoir de la résonance,entraînant des oscillations de grande amplitude. - Vibration forcée amortie (
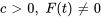 ) : c’est le cas le plus général, qui combine les effets de l’amortissement et de la force externe, induisant un comportement oscillatoire complexe.
) : c’est le cas le plus général, qui combine les effets de l’amortissement et de la force externe, induisant un comportement oscillatoire complexe.
D. Vibration libre non amortie
la forme la plus simple de vibration se produit lorsqu’il n’y a ni amortissement (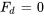 ), ni force externe. (
), ni force externe. (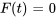 ). En ce cas, l’équation 3.8.1 se réduit à
). En ce cas, l’équation 3.8.1 se réduit à
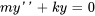 (3.8.2)
(3.8.2)
Cette équation est une équation différentielle linéaire homogène du second ordre. En résolvant l’équation caractéristique 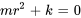 , on observe que les racines sont des racines complexes conjuguées données par
, on observe que les racines sont des racines complexes conjuguées données par
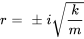
Le terme 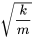 est la fréquence naturelle du système, indiquée par
est la fréquence naturelle du système, indiquée par 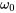 . La solution de l’équation est donc exprimée sous la forme
. La solution de l’équation est donc exprimée sous la forme
Il est souvent commode de représenter le déplacement sous forme d’amplitude-phase avec une seule fonction trigonométrique
Ici, 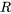 est l’amplitude de l’oscillation, donnée par
est l’amplitude de l’oscillation, donnée par 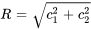 , et
, et 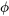 est l’angle de phase, qui peut être déterminé à partir des conditions initiales du système. L’angle de phase
est l’angle de phase, qui peut être déterminé à partir des conditions initiales du système. L’angle de phase 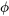 est généralement choisi de façon à satisfaire
est généralement choisi de façon à satisfaire 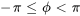 pour l’unicité et est lié à
pour l’unicité et est lié à 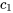 et
et 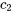 .
.
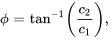
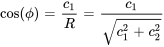 et
et 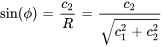
Le mouvement décrit par l’équation 3.8.4 est connu sous le nom de mouvement harmonique simple, caractérisé par sa nature sinusoïdale et sa fréquence constante. La période du mouvement est 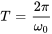 , représentant le temps qu’il faut pour effectuer un cycle complet.
, représentant le temps qu’il faut pour effectuer un cycle complet.
Considérations relatives aux unités et à l’angle de phase
- Unités : lorsque l’on travaille sur l’accélération due à la pesanteur ou sur toute autre grandeur physique, il est important d’utiliser des unités cohérentes tout au long du calcul. Dans le système métrique,
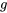 correspond généralement à
correspond généralement à 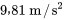 et les longueurs doivent être exprimées en mètres et les masses en kilogrammes. Dans le système impérial,
et les longueurs doivent être exprimées en mètres et les masses en kilogrammes. Dans le système impérial, 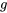 correspond à
correspond à , avec les longueurs en pieds et la masse en slugs.
, avec les longueurs en pieds et la masse en slugs. - Unicité des angles de phase : il existe une infinité d’angles de phase qui satisfont aux équations trigonométriques en raison de leur nature périodique. Cependant, la sélection de
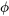 dans l’intervalle
dans l’intervalle  garantit l’obtention d’une solution dans un cycle complet. Les signes de
garantit l’obtention d’une solution dans un cycle complet. Les signes de 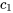 et
et 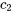 déterminent le quadrant dans lequel
déterminent le quadrant dans lequel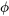 se trouve.
se trouve.
- Si
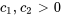 ,
, 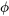 est dans le premier quadrant.
est dans le premier quadrant. - Si
 ,
, 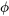 est dans le deuxième quadrant.
est dans le deuxième quadrant. - Si
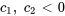 ,
, 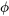 est dans le troisième quadrant.
est dans le troisième quadrant. - Si
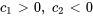 ,
, 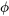 est dans le quatrième quadrant.
est dans le quatrième quadrant.
- Si
Un ressort vertical de 150 cm de long est suspendu à un plafond fixe. Un objet de 2 kg est attaché à l’extrémité inférieure du ressort, et le ressort s’allonge à 155 cm là où l’objet est en équilibre. L’objet est ensuite tiré vers le bas sur 3 cm supplémentaires, puis relâché avec une vitesse initiale de 20 cm/s vers le haut. En supposant qu’il n’y a pas d’amortissement et qu’aucune force extérieure autre que la gravité n’agit sur le système :
a) Déterminer le déplacement de l’objet en fonction du temps.
b) Déterminer la fréquence naturelle, la période et l’angle de phase du mouvement.
c) Réécrire l’équation du mouvement sous la forme amplitude-phase 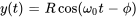 .
.
Exprimer les réponses en unités CGS, où  .
.
Afficher/Masquer la solution
Informations données :
- Longueur naturelle du ressort :
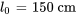
- Longueur à la position d’équilibre avec un objet de 2 kg attaché :
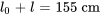
- Masse de l’objet :
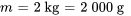
- Déplacement initial (descendant) :
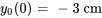
- Vitesse initiale (ascendante) :
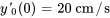
a)
Calculer la constante du ressort
À l’équilibre, les forces agissant sur l’objet sont équilibrées, de sorte que 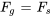 . Cela permet de déterminer la constante du ressort
. Cela permet de déterminer la constante du ressort  .
.
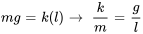
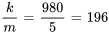
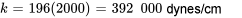
Calculer la fréquence naturelle :
La fréquence naturelle est

Il convient de noter que, pour trouver 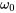 , nous avons besoin du ratio de
, nous avons besoin du ratio de  et de
et de 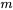 , et non de leurs valeurs individuelles.
, et non de leurs valeurs individuelles.
Trouver la solution générale :
Étant donné qu’il n’y a ni amortissement, ni force externe, le problème de valeur initiale est
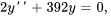
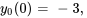
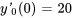
La solution générale de cette équation est donnée par l’équation 3.8.3.
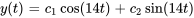
Appliquer les conditions initiales :
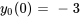
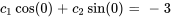
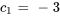
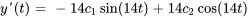
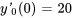
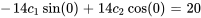
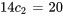
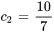
L’équation du déplacement de l’objet est donc
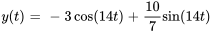
b)
Fréquence naturelle : 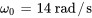
Période : 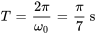
L’amplitude  est donnée par
est donnée par
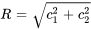
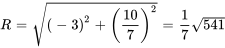
Angle de phase :
L’angle de phase de référence est déterminé par
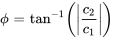
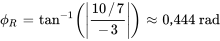
Puisque 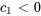 (
(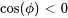 ) et
) et 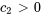 (
(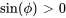 ),
), 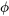 devrait se trouver dans le deuxième quadrant. Par conséquent,
devrait se trouver dans le deuxième quadrant. Par conséquent,
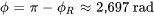 .
.
c) L’équation peut être rédigée sous la forme
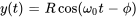

Le graphique du déplacement est montré pour les sept premières secondes.
Prenons un exemple
E. Vibration libre amortie
Dans une vibration libre amortie, il n’y a pas de force externe (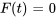 ). Partant, l’équation 3.8.1 est simplifiée en une équation différentielle linéaire homogène du second ordre.
). Partant, l’équation 3.8.1 est simplifiée en une équation différentielle linéaire homogène du second ordre.
Cette équation est une équation différentielle linéaire homogène du second ordre. En résolvant l’équation caractéristique 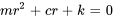 avec la formule quadratique, on trouve les racines
avec la formule quadratique, on trouve les racines
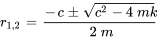
En fonction du discriminant 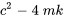 , on trouve trois types de mouvement :
, on trouve trois types de mouvement :
1. Amortissement critique (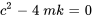 )
)
En ce cas, il y a une racine répétée 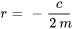 , de sorte que la solution générale de l’équation 3.8.5 devient
, de sorte que la solution générale de l’équation 3.8.5 devient
Ici, le mouvement subit un amortissement critique car l’amortissement est juste suffisant pour empêcher l’oscillation. Ce niveau d’amortissement est atteint lorsque le coefficient d’amortissement 
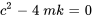
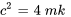
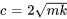
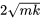 est appelé coefficient d’amortissement critique et est transcrit par
est appelé coefficient d’amortissement critique et est transcrit par 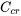 .
.
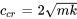
Il convient de noter que plus le temps passe ( ), plus le déplacement
), plus le déplacement 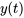 approche de zéro, indiquant que le système se stabilise rapidement et en douceur à sa position d’équilibre, sans oscillation ni dépassement de la position d’équilibre, comme le font les amortisseurs dans les systèmes de suspension automobiles.
approche de zéro, indiquant que le système se stabilise rapidement et en douceur à sa position d’équilibre, sans oscillation ni dépassement de la position d’équilibre, comme le font les amortisseurs dans les systèmes de suspension automobiles.
2. Suramortissement (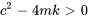 )
)
En ce cas, il y a deux racines réelles distinctes 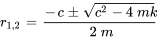 , toutes deux négatives. La solution générale de l’équation 3.8.5 devient
, toutes deux négatives. La solution générale de l’équation 3.8.5 devient
Comme 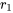 et
et 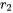 sont négatifs, plus le temps passe (
sont négatifs, plus le temps passe ( ), plus le déplacement
), plus le déplacement 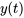 approche de zéro et le système revient graduellement à l’équilibre sans osciller. Il y a suramortissement lorsque
approche de zéro et le système revient graduellement à l’équilibre sans osciller. Il y a suramortissement lorsque 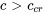 , typiquement souhaité dans les systèmes où le dépassement de la position d’équilibre, risque d’être néfaste ou indésirable, comme dans les équipements lourds. Les systèmes suramortis reviennent plus lentement à l’équilibre que les systèmes à amortissement critique. Cette réponse plus lente s’explique par la force d’amortissement plus élevée appliquée, qui empêche l’oscillation mais résiste également au mouvement, ce qui entraîne un retour lent.
, typiquement souhaité dans les systèmes où le dépassement de la position d’équilibre, risque d’être néfaste ou indésirable, comme dans les équipements lourds. Les systèmes suramortis reviennent plus lentement à l’équilibre que les systèmes à amortissement critique. Cette réponse plus lente s’explique par la force d’amortissement plus élevée appliquée, qui empêche l’oscillation mais résiste également au mouvement, ce qui entraîne un retour lent.
3. Sous-amortissement (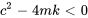 )
)
En ce cas, les racines de l’équation caractéristique sont des racines complexes conjuguées données par
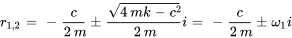
La solution générale de l’équation 3.8.5 est donc
Le terme  est lié à la fréquence d’oscillation. Comme pour le mouvement harmonique, on peut dériver la forme amplitude-phase de l’équation du mouvement.
est lié à la fréquence d’oscillation. Comme pour le mouvement harmonique, on peut dériver la forme amplitude-phase de l’équation du mouvement.
Là encore,
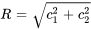 ,
, 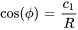 , et
, et 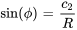
Un système sous-amorti se caractérise par un coefficient d’amortissement 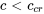 . Dans ce scénario, l’amortissement ne suffit pas à arrêter les oscillations, si bien que le système affiche un comportement oscillatoire autour de la position d’équilibre. L’amplitude de ces oscillations diminue au fil du temps, représentée par le terme variable dans le temps
. Dans ce scénario, l’amortissement ne suffit pas à arrêter les oscillations, si bien que le système affiche un comportement oscillatoire autour de la position d’équilibre. L’amplitude de ces oscillations diminue au fil du temps, représentée par le terme variable dans le temps 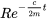 . Comme l’exposant
. Comme l’exposant 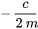 est toujours négatif,
est toujours négatif, 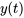 se rapproche graduellement de zéro au fil du temps (
se rapproche graduellement de zéro au fil du temps ( ). Il s’ensuit une réponse élastique du système à la moindre perturbation.
). Il s’ensuit une réponse élastique du système à la moindre perturbation.
Ce comportement est souvent celui qui est préféré dans diverses applications. Dans les instruments de musique, par exemple, les vibrations sous-amorties des cordes ou des membranes contribuent à produire un son soutenu et résonnant. De même, les amortisseurs sismiques dans les bâtiments utilisent une réponse sous-amortie contrôlée pour dissiper en toute sécurité l’énergie des tremblements de terre, ce qui permet aux structures d’osciller et de réduire les contraintes sans s’effondrer.
Une masse de 1 kg est attachée à un ressort d’une rigidité de 64 N/m et à un amortisseur avec une constante d’amortissement de 16 N.s/m. L’objet est comprimé à 20 cm au-dessus de son point d’équilibre, puis relâché avec une vitesse initiale de 2 m/s. Trouver le déplacement de l’objet en fonction du temps.
Afficher/Masquer la solution
Informations données :
- Masse de l’objet :
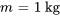
- Constante d’amortissement :
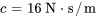
- Constante du ressort :
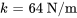
- Déplacement initial (ascendant) :
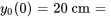
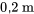
- Vitesse initiale (ascendante) :
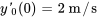
Le problème de valeur initiale pour ce système est
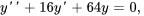

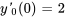
Avant de résoudre le PVI, on peut calculer le coefficient d’amortissement critique afin de déterminer le type d’amortissement.
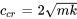
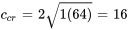
Le coefficient d’amortissement est égal au coefficient d’amortissement critique (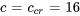 ), de sorte que le système présente un amortissement critique.
), de sorte que le système présente un amortissement critique.
Trouver la solution générale :
La solution générale d’un système à amortissement critique est donnée par l’équation 3.8.6.

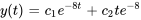
Appliquer les conditions initiales :
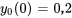
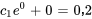
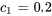
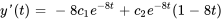
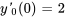
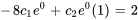
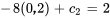

L’équation du déplacement de l’objet est donc
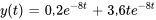
Le graphique du déplacement est montré au cours des trois premières secondes. Comme prévu, le système se déplace sans heurts et revient rapidement à sa position d’équilibre sans oscillation.

Prenons un exemple
Trouver le déplacement de l’objet dans l’exemple 3.8.2, avec un ressort maintenant attaché à un amortisseur avec une constante d’amortissement de 34 N.s/m.
Afficher/Masquer la solution
Informations données :
- Masse de l’objet :
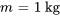
- Constante d’amortissement :

- Constante du ressort :
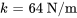
- Déplacement initial (ascendant) :
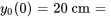
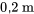
- Vitesse initiale (ascendante) :
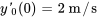
Le problème de valeur initiale pour ce système est
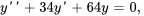

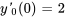
Dans l’exemple précédent, on a trouvé un coefficient d’amortissement critique de 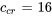 . Dans ce nouveau système, le coefficient d’amortissement est supérieur à sa valeur critique (
. Dans ce nouveau système, le coefficient d’amortissement est supérieur à sa valeur critique ( ), de sorte que le système est suramorti.
), de sorte que le système est suramorti.
Trouver la solution générale :
L’équation caractéristique pour cette équation différentielle a deux racines réelles distinctes.
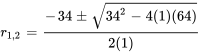


La solution générale d’un système suramorti est donnée par l’équation 3.8.7.
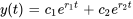
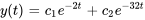
Appliquer les conditions initiales :
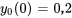
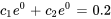
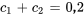

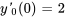
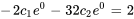
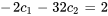
En résolvant le système pour les constantes 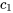 et
et 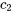 , on obtient
, on obtient
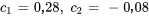
L’équation du déplacement de l’objet est donc
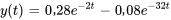
Le graphique ci-dessous montre le déplacement au cours des trois premières secondes. Il confirme que le système revient progressivement à sa position d’équilibre, en douceur et sans oscillation. Comparé au système à amortissement critique de l’exemple 3.8.2, ce système suramorti prend plus de temps à se stabiliser. Ce comportement plus lent souligne que l’augmentation de la force d’amortissement dans le système suramorti retarde le retour à l’équilibre.
Prenons un exemple
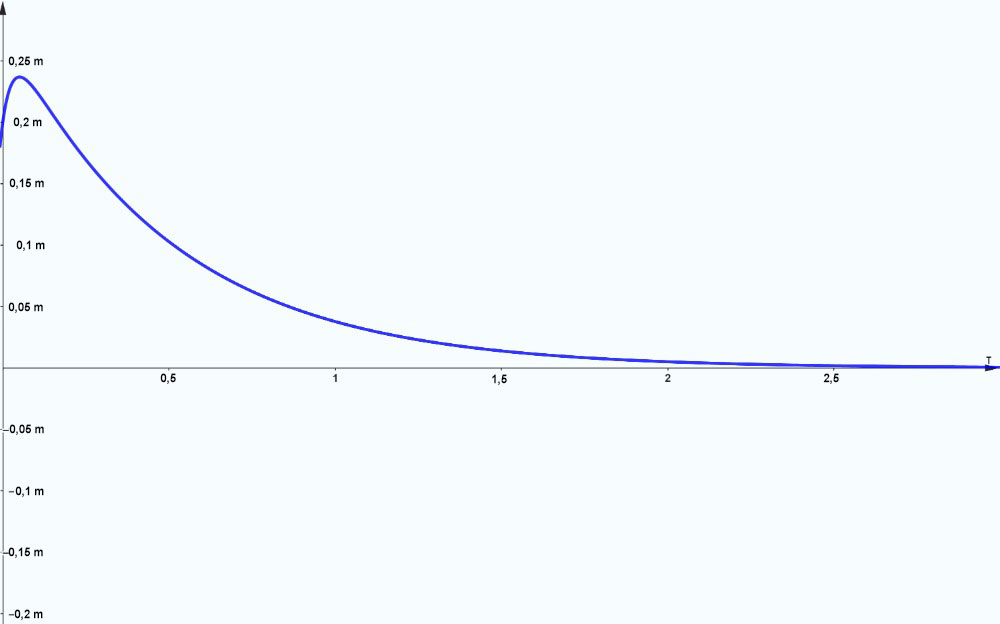
Trouver le déplacement de l’objet dans l’exemple 3.8.2, avec un ressort maintenant attaché à un amortisseur avec une constante d’amortissement de 4 N.s/m.
Afficher/Masquer la solution
Informations données :
- Masse de l’objet :
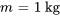
- Constante d’amortissement :
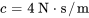
- Constante du ressort :
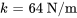
- Déplacement initial (ascendant) :
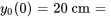
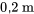
- Vitesse initiale (ascendante) :
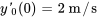
Le problème de valeur initiale pour ce système est


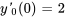
Dans l’exemple 3.8.2, on a trouvé un coefficient d’amortissement critique de 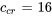 . Dans ce nouveau système, le coefficient d’amortissement est inférieur à sa valeur critique (
. Dans ce nouveau système, le coefficient d’amortissement est inférieur à sa valeur critique (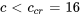 ), de sorte que le système est sous-amorti.
), de sorte que le système est sous-amorti.
Trouver la solution générale :
L’équation caractéristique pour cette équation différentielle a deux racines complexes conjuguées.

La solution générale d’un système sous-amorti est donnée par l’équation 3.8.8.
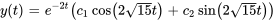
Appliquer les conditions initiales :
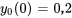
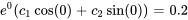
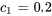
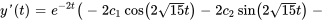
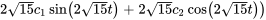
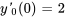
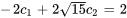

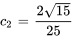
L’équation du déplacement de l’objet est donc

La forme amplitude-phase de l’équation est

Le graphique illustre le déplacement du système sur les trois premières secondes. Ce système sous-amorti n’est pas assez amorti pour stopper les oscillations, d’où un schéma d’oscillations décroissantes autour de la position d’équilibre. Ces oscillations diminuent en amplitude pendant environ deux secondes avant que le système ne se stabilise à la position d’équilibre.
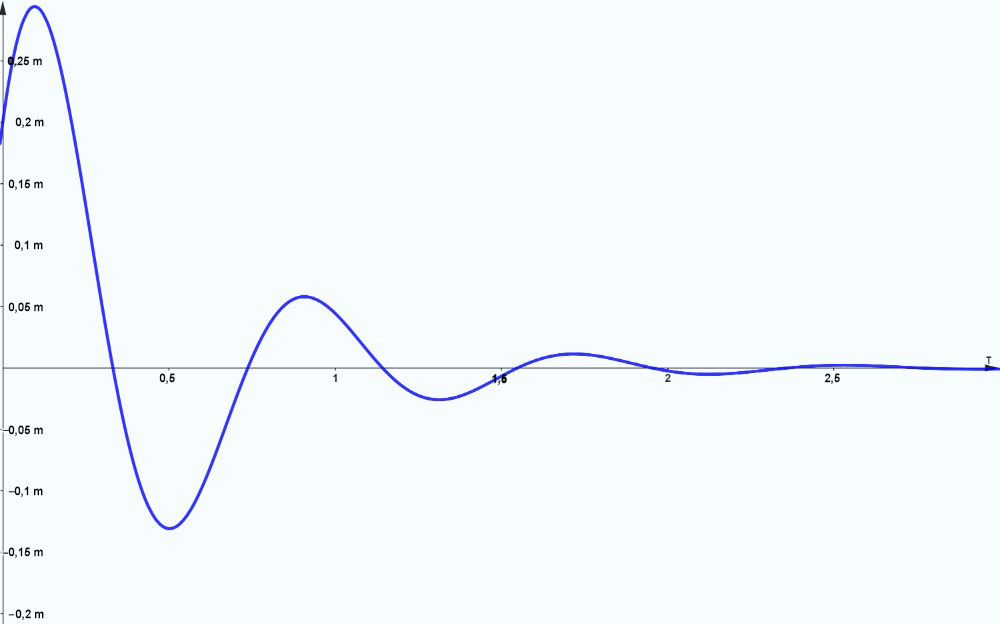
Prenons un exemple
F. Vibration forcée non amortie
Un système subit une vibration forcée non amortie lorsqu’il est soumis à une force externe, typiquement modélisée comme une fonction périodique telle que 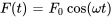 ou
ou 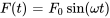 . Ces forces sinusoïdales proviennent généralement de mécanismes de rotation, de courants alternatifs ou d’autres phénomènes cycliques. L’équation du mouvement d’un tel système s’exprime comme suit
. Ces forces sinusoïdales proviennent généralement de mécanismes de rotation, de courants alternatifs ou d’autres phénomènes cycliques. L’équation du mouvement d’un tel système s’exprime comme suit
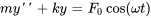
La solution générale de l’équation différentielle est
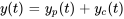
Ici, la solution comprend une partie complémentaire 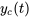 , qui représente la réponse vibratoire libre et non amortie, et une partie particulière
, qui représente la réponse vibratoire libre et non amortie, et une partie particulière  , qui représente la réponse du régime permanent à la fonction de forçage. La solution complémentaire, dictée par la fréquence naturelle du système
, qui représente la réponse du régime permanent à la fonction de forçage. La solution complémentaire, dictée par la fréquence naturelle du système 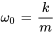 , est donnée par l’équation 3.8.3 :
, est donnée par l’équation 3.8.3 :
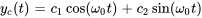
Pour déterminer la solution particulière, il faut normalement employer des méthodes telles que les coefficients indéterminés ou la variation des paramètres. Étant donné que l’on recherche la solution particulière, en fonction de la fréquence d’excitation oméga, on considère deux cas :
1. Sans résonance (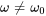 ) : lorsque la fréquence d’excitation est différente de la fréquence naturelle, la solution particulière prend la forme
) : lorsque la fréquence d’excitation est différente de la fréquence naturelle, la solution particulière prend la forme
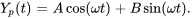
Pour trouver les valeurs spécifiques des coefficients A et B, on utilise la méthode des coefficients indéterminés. Une fois ces coefficients déterminés, la solution particulière peut être exprimée sous la forme
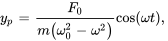
et la solution générale est
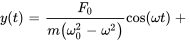
 (3.8.10)
(3.8.10)
La fonction de déplacement est constituée de composantes sinusoïdales et cosinusoïdales d’amplitude limitée.
2. Avec résonance ( ) : lorsque la fréquence d’excitation est égale à la fréquence naturelle, la solution particulière prend la forme
) : lorsque la fréquence d’excitation est égale à la fréquence naturelle, la solution particulière prend la forme
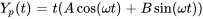
En utilisant la méthode des coefficients indéterminés et après avoir déterminé les coefficients, la solution particulière peut être exprimée sous la forme
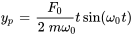
La solution générale est donc
En ce cas, la solution particulière comporte un facteur temporel  , indiquant la hausse illimitée de l’amplitude. Ce phénomène, connu sous le nom de résonance, augmente considérablement l’amplitude des oscillations et présente des risques potentiels, notamment de défaillance mécanique due à des oscillations excessives.
, indiquant la hausse illimitée de l’amplitude. Ce phénomène, connu sous le nom de résonance, augmente considérablement l’amplitude des oscillations et présente des risques potentiels, notamment de défaillance mécanique due à des oscillations excessives.
L’amplitude des oscillations dans une vibration forcée est sensible à la relation entre la fréquence d’excitation et la fréquence naturelle du système. Lorsque la fréquence d’excitation se rapproche de la fréquence naturelle, l’amplitude augmente et atteint son pic au moment de la résonance. Cette sensibilité est un facteur clé dans la conception des structures et des systèmes, le but étant d’éviter que leurs fréquences naturelles soient alignées sur les fréquences des forces environnementales courantes, comme le vent ou la circulation. Un tel alignement pourrait déclencher une résonance, mettant en péril l’intégrité de la structure.
Cela étant, il existe des applications spécifiques qui tirent avantage de l’induction de la résonance, par exemple dans les filtres et les capteurs mécaniques, où la résonance peut améliorer la sensibilité ou l’intensité du signal.
Un objet de 32 livres (lb) est suspendu à un ressort, qu’il faut étirer de 6 pouces (inches) pour atteindre l’équilibre. Ce système non amorti est soumis à une force externe 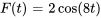 et subit une résonance. Au départ, l’objet est déplacé de 3 pouces au-dessous de la position d’équilibre et reçoit une vitesse ascendante de 1 pied par seconde (ft/s). Déterminer le déplacement de l’objet dans ces conditions.
et subit une résonance. Au départ, l’objet est déplacé de 3 pouces au-dessous de la position d’équilibre et reçoit une vitesse ascendante de 1 pied par seconde (ft/s). Déterminer le déplacement de l’objet dans ces conditions.
Afficher/Masquer la solution
Informations données :
- Masse de l’objet :
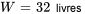
- Déplacement du ressort à l’équilibre :
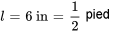
- Force externe :
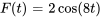
- Déplacement initial (descendant) :
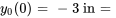

- Vitesse initiale (ascendante) :
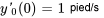
Calculer la constante du ressort
Dans le système britannique, le poids est généralement exprimé en livres (pounds). Pour trouver la constante du ressort, il faut d’abord convertir le poids en masse au moyen de la formule
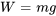
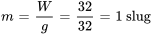
À l’équilibre, 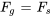 . Cette relation permet de calculer la constante du ressort
. Cette relation permet de calculer la constante du ressort  .
.
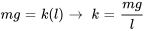
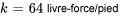
Calculer la fréquence naturelle :
La fréquence naturelle est
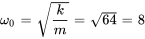
Par ailleurs, si le système résonne à une fréquence d’excitation de 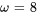 (à partir de
(à partir de 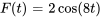 ), cette fréquence de résonance devrait correspondre à la fréquence naturelle du système, réaffirmant que
), cette fréquence de résonance devrait correspondre à la fréquence naturelle du système, réaffirmant que  .
.
Trouver la solution générale :
Le problème de valeur initiale pour ce système est
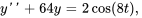
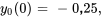

La solution générale d’un système subissant une résonance est donnée par l’équation 3.8.11.
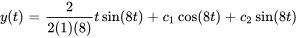
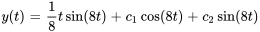
Appliquer les conditions initiales :

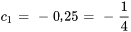
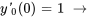

L’équation du déplacement de l’objet est donc
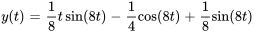
La solution complémentaire peut être écrite sous la forme amplitude-phase, en combinant les deux derniers termes.

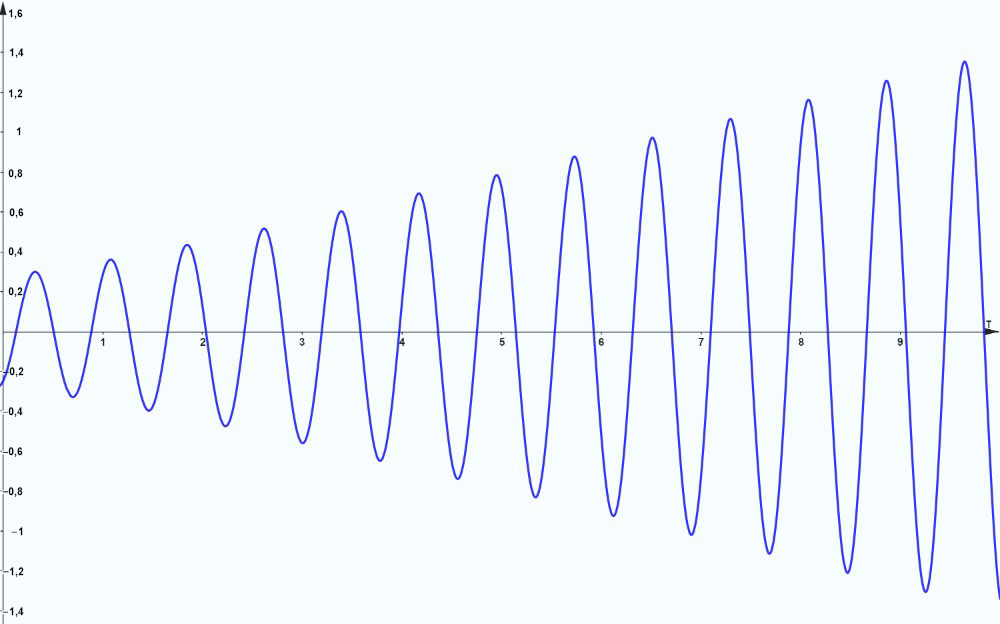
Le graphique montre l’évolution du déplacement du système au cours des dix premières secondes. Comme la solution particulière inclut un facteur temps (t), l’amplitude du déplacement tend à devenir infiniment grande au fur et à mesure que le temps progresse vers l’infini. Cependant, dans la réalité, la plupart des systèmes subissent un certain amortissement. Même une petite dose d’amortissement peut avoir une incidence significative sur l’amplitude et le comportement du système, en particulier autour des fréquences de résonance, empêchant la croissance illimitée de l’amplitude dépeinte dans les modèles idéaux.
Prenons un exemple
G. Vibration forcée amortie
C’est le cas le plus général, qui combine les effets de l’amortissement et de la force externe. Le mouvement d’un tel système est régi par
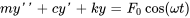
La solution de l’équation différentielle est la somme des solutions complémentaire et particulière.
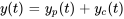
La solution complémentaire est la solution du comportement libre et amorti, tandis que la solution particulière est trouvée en utilisant la méthode des coefficients indéterminés ou de la variation des paramètres.
Compte tenu de notre connaissance des vibrations libres amorties, nous savons que, à mesure que le temps progresse vers l’infini, la solution complémentaire se rapproche de zéro. Par conséquent, le déplacement du système reflète de plus en plus le comportement de la solution particulière. Par conséquent, dans l’analyse vibratoire, la solution complémentaire est communément appelée régime transitoire, reflétant la réponse initiale, tandis que la solution particulière est connue sous le nom de régime permanent, illustrant la réponse continue à la force externe.
Trouver le déplacement de l’objet dans l’exemple 3.8.5, avec un ressort maintenant attaché à un amortisseur avec une constante d’amortissement de 34 lb/.s/ft
Afficher/Masquer la solution
Informations données :
- Masse de l’objet :
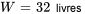
- Déplacement du ressort à l’équilibre :
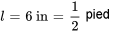
- Constante d’amortissement :
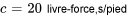
- Force externe :
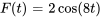
- Déplacement initial (descendant) :
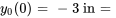

- Vitesse initiale (ascendante) :
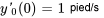
Dans l’exemple précédent, on a déterminé la constante du ressort : 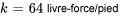 . Le problème de valeur initiale pour ce système est
. Le problème de valeur initiale pour ce système est
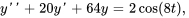
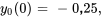

Étant donné que l’équation a deux racines réelles distinctes 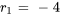 et
et  , la solution complémentaire, d’après l’équation 3.8.7, est
, la solution complémentaire, d’après l’équation 3.8.7, est
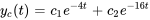
Trouver la solution particulière :
Pour trouver la solution particulière, il faut utiliser la méthode des coefficients indéterminés. Compte tenu de la fonction cosinus de forçage, on suppose que la forme de la solution particulière est
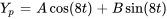
Les dérivées sont
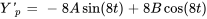
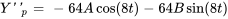
En remplaçant 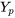 et ses dérivées dans l’équation différentielle, on obtient
et ses dérivées dans l’équation différentielle, on obtient
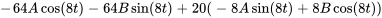
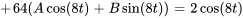
En simplifiant, on obtient
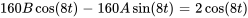
En faisant correspondre les coefficients des termes sinus et cosinus, on obtient


La solution particulière est donc
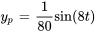
En combinant les solutions particulière et complémentaire, on obtient la solution générale
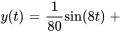
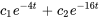
Appliquer les conditions initiales :

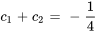
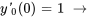
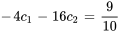
En résolvant le système, on obtient les constantes
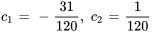
L’équation du déplacement de l’objet est donc
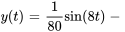
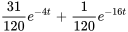
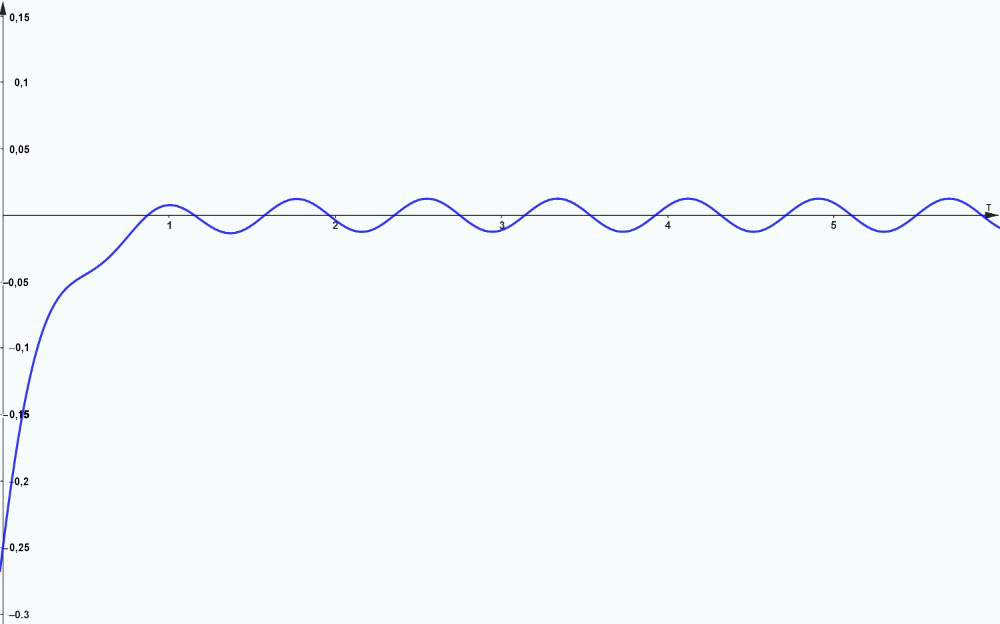
Le graphique représente l’évolution du déplacement du système au cours des six premières secondes. Initialement, pendant la première seconde environ, le déplacement est principalement influencé par la solution complémentaire, ce qui reflète la phase transitoire. Après cette période initiale, le déplacement s’aligne de plus en plus sur la solution périodique particulière, représentant le comportement du système en régime permanent.
Prenons un exemple
Section 3.8 Exercices
- Un objet attaché à un ressort subit un mouvement harmonique simple modélisé par l’équation différentielle
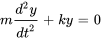
où
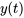 est le déplacement de la masse (par rapport à l’équilibre) à l’instant
est le déplacement de la masse (par rapport à l’équilibre) à l’instant  ,
, 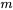 est la masse de l’objet et
est la masse de l’objet et  est la constante du ressort. Une masse de
est la constante du ressort. Une masse de  étire le ressort de
étire le ressort de 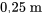 . a) Utilise cette information pour trouver la constante du ressort. (Utilise
. a) Utilise cette information pour trouver la constante du ressort. (Utilise 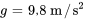 ). b) La masse est détachée du ressort et une nouvelle masse de
). b) La masse est détachée du ressort et une nouvelle masse de 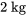 est attachée. Cette masse est déplacée de
est attachée. Cette masse est déplacée de 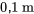 au-dessus du point d’équilibre (le dessus est positif et le dessous est négatif), puis lancée à une vitesse initiale de
au-dessus du point d’équilibre (le dessus est positif et le dessous est négatif), puis lancée à une vitesse initiale de 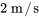 . Rédige l’équation du mouvement sous la forme
. Rédige l’équation du mouvement sous la forme 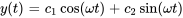 . Ne laisse aucune constante inconnue dans votre équation.
. Ne laisse aucune constante inconnue dans votre équation.Afficher/Masquer la réponse
a)
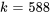 N/m
N/mb)
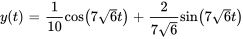
- Un objet de
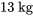 est attaché à un ressort avec une constante du ressort de
est attaché à un ressort avec une constante du ressort de 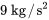 . Il est également attaché à un amortisseur à constante d’amortissement de
. Il est également attaché à un amortisseur à constante d’amortissement de 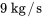 . L’objet est initialement déplacé de
. L’objet est initialement déplacé de 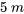 au-dessus du point d’équilibre, puis relâché. a) Trouve son déplacement pour
au-dessus du point d’équilibre, puis relâché. a) Trouve son déplacement pour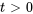 . b) Décris le mouvement.
. b) Décris le mouvement.
Afficher/Masquer la réponse
a)
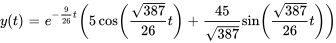
b) Vibration libre non amortie
- Un objet de
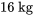 est attaché à un ressort avec une constante du ressort de
est attaché à un ressort avec une constante du ressort de 
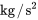 . Il est également attaché à un amortisseur à constante d’amortissement de
. Il est également attaché à un amortisseur à constante d’amortissement de 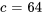
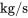 . L’objet est tiré de
. L’objet est tiré de  vers le bas, puis relâché à une vitesse ascendante initiale de
vers le bas, puis relâché à une vitesse ascendante initiale de  . Trouve le déplacement de l’objet. Pars du principe que le déplacement et la vitesse sont positifs et ascendants.
. Trouve le déplacement de l’objet. Pars du principe que le déplacement et la vitesse sont positifs et ascendants.
Afficher/Masquer la réponse