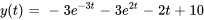3.4 Méthode des coefficients indéterminés
La méthode des coefficients indéterminés est une technique permettant de trouver des solutions particulières, 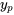 à des équations différentielles linéaires non homogènes à coefficients constants
à des équations différentielles linéaires non homogènes à coefficients constants
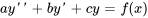
Pour appliquer cette méthode, il faut d’abord identifier la forme de la fonction de forçage 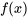 , puis faire une supposition raisonnée de
, puis faire une supposition raisonnée de 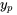 avec des coefficients indéterminés. Cette supposition est ensuite remplacée dans l’équation pour trouver la valeur de ces coefficients. Cette méthode est utile lorsque la fonction de forçage,
avec des coefficients indéterminés. Cette supposition est ensuite remplacée dans l’équation pour trouver la valeur de ces coefficients. Cette méthode est utile lorsque la fonction de forçage, 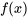 , est une fonction relativement simple, comme un polynôme, une exponentielle, un sinus ou un cosinus, ou une combinaison de ces fonctions.
, est une fonction relativement simple, comme un polynôme, une exponentielle, un sinus ou un cosinus, ou une combinaison de ces fonctions.
Fonctions de forçage polynomiales : Pour 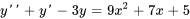 , nous ne connaissons pas de solution particulière. Mais, en regardant
, nous ne connaissons pas de solution particulière. Mais, en regardant 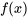 , on se demande quel type de fonction laisserait un polynôme. Supposons
, on se demande quel type de fonction laisserait un polynôme. Supposons 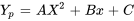 et trouvons la valeur de
et trouvons la valeur de 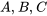 .
.
Fonctions de forçage exponentielles : Pour 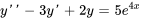 , nous supposons
, nous supposons 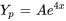 . Si
. Si 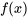 était
était 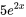 , il faudrait multiplier notre supposition par
, il faudrait multiplier notre supposition par  :
: 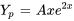 .
.
Ajuster la supposition en fonction des solutions d’équations complémentaires : Si l’équation complémentaire a une solution correspondant partiellement à 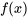 , il faut ajuster la supposition en conséquence. Par exemple, si
, il faut ajuster la supposition en conséquence. Par exemple, si 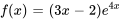 , il faut commencer par
, il faut commencer par 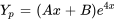 . Si
. Si 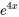 est une solution à l’équation non homogène, il faut utiliser
est une solution à l’équation non homogène, il faut utiliser 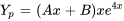 . Pour une racine répétée, utiliser
. Pour une racine répétée, utiliser 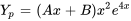 .
.
Remarque : nous transcrivons 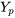 avec un « Y » majuscule pour indiquer qu’il s’agit de notre supposition initiale pour la solution particulière. En revanche,
avec un « Y » majuscule pour indiquer qu’il s’agit de notre supposition initiale pour la solution particulière. En revanche, 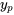 avec un « y » minuscule indique la solution particulière après détermination des coefficients.
avec un « y » minuscule indique la solution particulière après détermination des coefficients.
Trouver la solution générale de l’équation suivante.
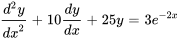
Afficher/Masquer la solution
Trouver la solution complémentaire :
Bien qu’il ne soit pas nécessaire de connaître la solution complémentaire pour trouver la solution particulière, il est utile de la connaître. Comprendre la solution complémentaire permet de faire de meilleures suppositions initiales pour la solution particulière et de les ajuster en conséquence avant de procéder à l’algèbre nécessaire pour déterminer les coefficients indéterminés.
L’équation auxiliaire associée à l’équation complémentaire est 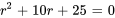 , qui a une racine répétée
, qui a une racine répétée 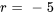 . Ainsi,
. Ainsi, 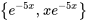 est un ensemble fondamental de solutions de l’équation complémentaire.
est un ensemble fondamental de solutions de l’équation complémentaire.
Supposer la forme de la solution particulière :
Étant donné que 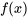 est une fonction exponentielle et que les fonctions exponentielles ne changent jamais d’exposant ou ne disparaissent jamais par différenciation, nous supposons que la solution particulière aura une forme similaire à la composante exponentielle dans
est une fonction exponentielle et que les fonctions exponentielles ne changent jamais d’exposant ou ne disparaissent jamais par différenciation, nous supposons que la solution particulière aura une forme similaire à la composante exponentielle dans 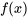 . De même, l’exposant dans
. De même, l’exposant dans 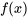 diffère de l’exposant dans la solution complémentaire, de sorte qu’aucun ajustement n’est nécessaire.
diffère de l’exposant dans la solution complémentaire, de sorte qu’aucun ajustement n’est nécessaire.
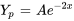
Introduire la supposition dans l’équation pour trouver A :
Il faut ensuite introduire la supposition et ses dérivées dans l’équation différentielle afin de déterminer le coefficient indéterminé A.
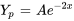 ,
, 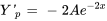 ,
, 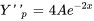
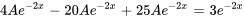
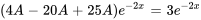
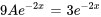
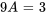
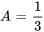
La solution particulière de l’équation différentielle est donc
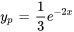
Trouver la solution générale :
La solution générale d’une équation non homogène est
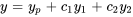 .
.
où 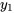 et
et 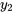 sont les solutions de l’équation complémentaire et
sont les solutions de l’équation complémentaire et 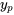 est la solution particulière de l’équation non homogène.
est la solution particulière de l’équation non homogène.
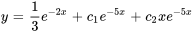
Prenons un exemple
Trouver la solution générale de l’équation suivante.
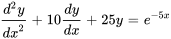
Afficher/Masquer la solution
Trouver la solution complémentaire :
L’équation complémentaire est similaire à celle de l’exemple 3.4.2. Ainsi, 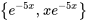 est un ensemble fondamental de solutions de l’équation complémentaire et la solution complémentaire est
est un ensemble fondamental de solutions de l’équation complémentaire et la solution complémentaire est 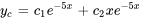 .
.
Supposer la forme de la solution particulière :
Notre supposition initiale est 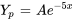 . Cependant, comme
. Cependant, comme 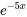 est aussi la solution complémentaire, il faut ajuster notre supposition. Étant donné que
est aussi la solution complémentaire, il faut ajuster notre supposition. Étant donné que 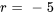 est une racine répétée, nous multiplions notre suppositions originale par
est une racine répétée, nous multiplions notre suppositions originale par 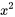 .
.
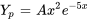
Introduire la supposition dans l’équation pour trouver A :
Il faut ensuite introduire la supposition et ses dérivées dans l’équation différentielle afin de déterminer le coefficient indéterminé A.
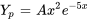 ,
,
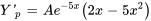 ,
,
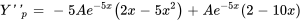
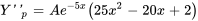
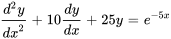
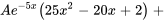
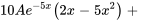
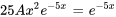
En factorisant le terme exponentiel et en rassemblant les termes semblables, on obtient
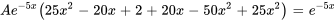
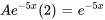
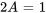
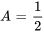
La solution particulière de l’équation différentielle est donc
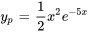
Trouver la solution générale :
La solution générale est
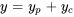
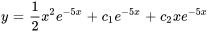
Prenons un exemple
Résoudre le problème de valeur initiale suivant.
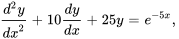
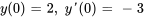
Afficher/Masquer la solution
Trouver la solution générale :
L’équation est similaire à celle de l’exemple 3.4.3. La solution générale est donc
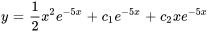
Appliquer les conditions initiales :
Appliquer la condition initiale à  :
:
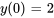
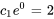
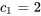
Appliquer la condition initiale à 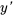 :
:
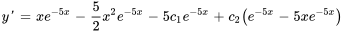
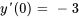
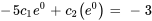
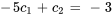
En introduisant cela dans 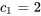 , on obtient
, on obtient 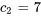 .
.
La solution du problème de valeur initiale est donc
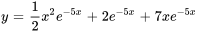
Remarque : les conditions initiales doivent satisfaire la solution tout entière de l’équation non homogène, et non pas seulement la partie complémentaire. Il faut donc appliquer les conditions initiales directement à la solution générale de l’équation non homogène donnée pour déterminer les constantes.
La section suivante synthétise les formes appropriées de supposition pour différents types de fonctions de forçage et explique comment modifier ces suppositions si une partie quelconque de la fonction de forçage  correspond à des solutions de l’équation complémentaire.
correspond à des solutions de l’équation complémentaire.
Méthode des coefficients indéterminés (supposition de  )
)
Trouver une solution particulière à l’équation différentielle
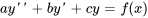
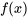 |
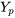 Supposition Supposition |
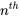 degré polynomial degré polynomial |
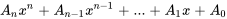 |
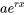 |
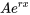 |
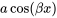 |
 |
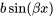 |
 |
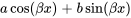 |
 |
Remarques
1. Produits exponentiels et polynomiaux : Si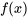 ne contient que des fonctions exponentielles ou des produits de fonction exponentielle et des polynômes et si
ne contient que des fonctions exponentielles ou des produits de fonction exponentielle et des polynômes et si 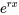 est aussi la solution de l’équation complémentaire associée, il faut alors multiplier la partie exponentielle de
est aussi la solution de l’équation complémentaire associée, il faut alors multiplier la partie exponentielle de 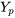 par
par  pour une racine simple
pour une racine simple 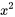 pour une racine répétée.
pour une racine répétée.
2. Racines complexes : Si 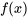 a trait à la racine complexe d’une équation complémentaire, c’est-à-dire si
a trait à la racine complexe d’une équation complémentaire, c’est-à-dire si  est une racine complexe de l’équation auxiliaire associée, il faut alors multiplier la supposition
est une racine complexe de l’équation auxiliaire associée, il faut alors multiplier la supposition 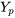 par
par  .
.
3. Produits exponentiels et trigonométriques/polynomiaux : Si 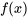 comprend des produits d’une fonction exponentielle et une fonction polynomiale ou trigonométrique, il ne faut retenir que la partie polynomiale ou trigonométrique de la supposition initiale, puis multiplier par la partie exponentielle de
comprend des produits d’une fonction exponentielle et une fonction polynomiale ou trigonométrique, il ne faut retenir que la partie polynomiale ou trigonométrique de la supposition initiale, puis multiplier par la partie exponentielle de 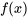 .
.
4. Produits polynomiaux et trigonométriques : Si 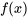 comprend des produits de fonctions polynomiales et trigonométriques, il faut d’abord noter la supposition pour la fonction polynomiale uniquement, puis multiplier par le cosinus approprié, puis ajouter une autre fonction polynomiale supposée avec différents coefficients et multiplier par le sinus approprié.
comprend des produits de fonctions polynomiales et trigonométriques, il faut d’abord noter la supposition pour la fonction polynomiale uniquement, puis multiplier par le cosinus approprié, puis ajouter une autre fonction polynomiale supposée avec différents coefficients et multiplier par le sinus approprié.
Trouver la forme d’une solution particulière à
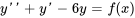
où 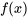 est
est
a) 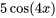 b)
b) 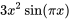 c)
c) 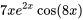 d)
d) 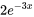 e)
e) 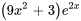
Afficher/Masquer la solution
L’équation auxiliaire associée à l’équation est 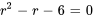 , qui a pour racines
, qui a pour racines 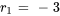 et
et 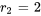 .
.
a) 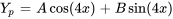
b) Cette fonction comprend le produit de fonctions polynomiales (second degré) et trigonométriques. Suivant la remarque 4, il faut d’abord supposer le polynôme et le multiplier par le bon cosinus, puis l’ajouter au produit d’un autre polynôme supposé avec différents coefficients et un sinus.
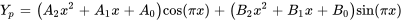
b) Cette fonction comprend le produit de fonctions exponentielles, polynomiales (premier degré) et trigonométriques. Suivant les remarques 3 et 4, il faut d’abord supposer le polynôme et le multiplier par le bon cosinus, puis l’ajouter au produit d’un autre polynôme supposé avec différents coefficients et un sinus. Enfin, il faut multiplier la partie exponentielle
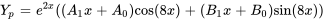
d) Étant donné que 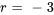 est la racine de l’équation auxiliaire et donc que
est la racine de l’équation auxiliaire et donc que 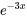 est une solution de l’ensemble fondamental,
est une solution de l’ensemble fondamental, 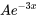 n’est pas une supposition correcte. Suivant la remarque 1, il faut le multiplier par
n’est pas une supposition correcte. Suivant la remarque 1, il faut le multiplier par  . Par conséquent,
. Par conséquent,
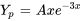
b) Cette fonction comprend le produit de fonctions exponentielles et polynomiales (second degré). Suivant la remarque 3, il faut d’abord supposer le polynôme et multiplier la partie exponentielle. La supposition polynomiale sera 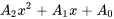 . La partie exponentielle
. La partie exponentielle 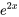 doit être multipliée par
doit être multipliée par  car
car 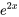 est dans l’ensemble fondamental de solutions (remarque 1). Par conséquent,
est dans l’ensemble fondamental de solutions (remarque 1). Par conséquent,
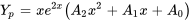
Prenons un exemple
Section 3.4 Exercices
- Trouve la solution particulière de l’EDO
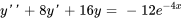
Afficher/Masquer la réponse
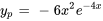
- Trouve la solution générale de l’EDO
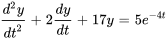
Afficher/Masquer la réponse
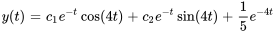
- Trouve la solution particulière de l’EDO
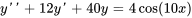
Afficher/Masquer la réponse
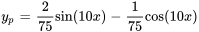
- Résous le problème de valeur initiale
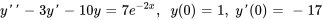
Afficher/Masquer la réponse

- Résous le problème de valeur initiale
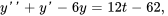
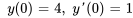
Afficher/Masquer la réponse