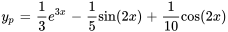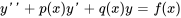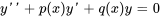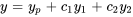3.3 Équations différentielles linéaires non homogènes du second ordre
A. Solution générale d’équations non homogènes
Dans cette section, nous explorons les équations différentielles linéaires non homogènes du second ordre de la forme :
Théorème d’unicité des solutions. Si 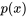 et
et 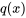 sont continus sur un intervalle ouvert
sont continus sur un intervalle ouvert 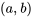 et si
et si 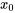 est dans l’intervalle, alors le problème de valeur initiale a une solution unique dans
est dans l’intervalle, alors le problème de valeur initiale a une solution unique dans 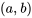 .
.
Pour résoudre l’équation 3.3.1, il faut d’abord trouver les solutions de l’équation homogène associée
L’équation 3.3.2 est l’équation complémentaire à l’équation 3.3.1.
Théorème des solutions générales. 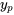 est une solution particulière de l’équation non homogène 3.3.1 et
est une solution particulière de l’équation non homogène 3.3.1 et 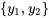 est un ensemble fondamental de solutions à l’équation complémentaire 3.3.2. La solution générale de l’équation non homogène est donc
est un ensemble fondamental de solutions à l’équation complémentaire 3.3.2. La solution générale de l’équation non homogène est donc
Ici,  représente la solution de l’équation complémentaire associée, communément exprimée
représente la solution de l’équation complémentaire associée, communément exprimée 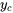 . L’équation 3.3.3 est donc souvent exprimée comme suit :
. L’équation 3.3.3 est donc souvent exprimée comme suit :
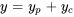
B. Principe de superposition
Le principe de superposition est un outil puissant qui permet de simplifier la résolution d’équations non homogènes. Il consiste à diviser la fonction de forçage en composantes plus simples, à trouver une solution particulière pour chaque composante, puis à additionner ces solutions pour obtenir une solution complète à l’équation d’origine.
Théorème. Si 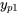 est une solution particulière de l’équation différentielle
est une solution particulière de l’équation différentielle
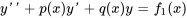
et si 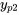 est une solution particulière de l’équation différentielle
est une solution particulière de l’équation différentielle
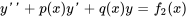
alors, pour n’importe quelle constante 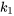 et
et 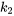 ,
, 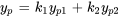 est une solution particulière de l’équation différentielle
est une solution particulière de l’équation différentielle
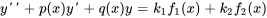
Étant donné que 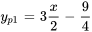 est une solution particulière de
est une solution particulière de 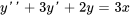 (i) et
(i) et 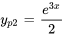 est une solution particulière de
est une solution particulière de 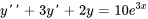 (ii), trouver une solution particulière de
(ii), trouver une solution particulière de 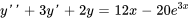 (iii).
(iii).
Afficher/Masquer la solution
- Fonction de forçage de l’équation (i) :
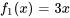
- Fonction de forçage de l’équation (ii) :
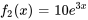
- Fonction de forçage de l’équation (iii) :
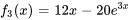
Si l’on regarde le côté droit des équations, on remarque que 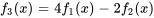 . Par conséquent, la même combinaison linéaire de
. Par conséquent, la même combinaison linéaire de 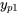 et
et 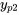 donne une solution particulière pour l’équation (iii) :
donne une solution particulière pour l’équation (iii) :
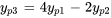
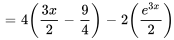
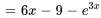
Prenons un exemple
Section 3.3 Exercices
- Étant donné que
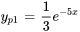 est une solution particulière de
est une solution particulière de 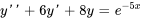 et que
et que 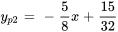 est une solution particulière de
est une solution particulière de 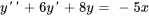 , utilise la méthode de la superposition pour trouver une solution particulière à
, utilise la méthode de la superposition pour trouver une solution particulière à
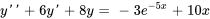
Afficher/Masquer la réponse
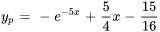
- Étant donné que
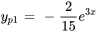 est une solution particulière de
est une solution particulière de 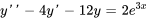 et que
et que 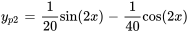 est une solution particulière de
est une solution particulière de 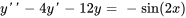 , utilise la méthode de la superposition pour trouver une solution particulière à
, utilise la méthode de la superposition pour trouver une solution particulière à
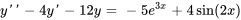
Afficher/Masquer la réponse