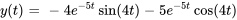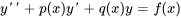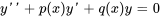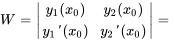3.1 Équations différentielles linéaires homogènes du second ordre
Les équations différentielles linéaires du second ordre présentent cette forme :
Ici,  est la fonction que nous recherchons et
est la fonction que nous recherchons et  ,
, 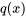 et
et  sont des fonctions connues. Dans le cas d’équations non homogènes,
sont des fonctions connues. Dans le cas d’équations non homogènes,  est ce que l’on appelle la fonction de forçage, représentant des forces ou influences externes. Commençons par le cas homogène, où
est ce que l’on appelle la fonction de forçage, représentant des forces ou influences externes. Commençons par le cas homogène, où 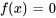 , nous explorerons le cas non homogène plus tard.
, nous explorerons le cas non homogène plus tard.
Théorème d’unicité des solutions. Si  et
et 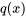 sont continus sur un intervalle ouvert
sont continus sur un intervalle ouvert 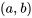 , alors le problème de valeur initiale a une solution unique dans cet intervalle.
, alors le problème de valeur initiale a une solution unique dans cet intervalle.
Théorème de combinaison linéaire. Supposons que 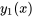 et
et 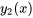 sont deux solutions de l’équation homogène 3.1.2 sur un intervalle ouvert
sont deux solutions de l’équation homogène 3.1.2 sur un intervalle ouvert 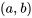 . En ce cas, n’importe quelle combinaison linéaire
. En ce cas, n’importe quelle combinaison linéaire 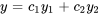 constitue également une solution sur le même intervalle.
constitue également une solution sur le même intervalle.
Toutes ces solutions, et
et  , forment un ensemble fondamental ou une base pour l’espace des solutions si elles sont linéairement indépendantes. Partant, n’importe quelle solution à l’équation 3.1.2 peut être exprimée comme une combinaison linéaire de
, forment un ensemble fondamental ou une base pour l’espace des solutions si elles sont linéairement indépendantes. Partant, n’importe quelle solution à l’équation 3.1.2 peut être exprimée comme une combinaison linéaire de  et
et  . Le wronskien, W, est crucial pour déterminer l’indépendance linéaire. Pour
. Le wronskien, W, est crucial pour déterminer l’indépendance linéaire. Pour  et
et  , le wronskien en tout
, le wronskien en tout 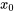 dans
dans  doit être non nul pour confirmer l’indépendance :
doit être non nul pour confirmer l’indépendance :
Théorème d’indépendance linéaire. Si  et
et 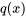 sont continus sur
sont continus sur 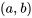 et si
et si  et
et  sont des solutions, alors elles sont linéairement indépendantes sur
sont des solutions, alors elles sont linéairement indépendantes sur 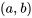 si et uniquement si le wronskien W n’est nulle part égal à zéro sur
si et uniquement si le wronskien W n’est nulle part égal à zéro sur 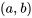 .
.
Théorème d’Abel. Si  et
et 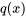 sont continus sur
sont continus sur 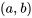 et si
et si 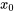 est n’importe quel point dans
est n’importe quel point dans 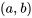 , alors le wronskien
, alors le wronskien 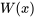 est donné par :
est donné par :
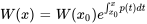
Le théorème d’Abel constitue un outil puissant pour analyser le comportement de solutions sur un intervalle, stipulant que si le wronskien n’est pas nul en un point et si  est continu, alors le wronskien reste non nul dans tout l’intervalle.
est continu, alors le wronskien reste non nul dans tout l’intervalle.
Théorème d’équivalence : Lorsque  et
et 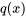 sont continus sur
sont continus sur 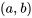 , et compte tenu de deux solutions
, et compte tenu de deux solutions  et
et  à l’équation 3.1.2, les solutions suivantes sont équivalentes :
à l’équation 3.1.2, les solutions suivantes sont équivalentes :
- la solution générale de l’équation sur
 est
est 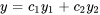
-
 est un ensemble fondamental de solutions de l’équation sur
est un ensemble fondamental de solutions de l’équation sur 
-
 est linéairement indépendant sur
est linéairement indépendant sur 
- Le wronskien de
 n’est pas nul en un point dans
n’est pas nul en un point dans 
- Le wronskien de
 n’est pas nul à tous les points dans
n’est pas nul à tous les points dans 
Grâce à ces théorèmes fondamentaux, nous disposons des outils nécessaires pour commencer à résoudre des équations différentielles linéaires homogènes du second ordre et nous préparer aux complexités des cas non homogènes.
Les deux solutions de l’équation différentielle 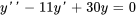 sont
sont 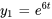 et
et 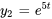 .
.
a) Trouver le wronskien des solutions et déterminer si elles sont linéairement indépendantes.
b) Trouver la solution générale de l’équation différentielle.
c) Trouver la solution satisfaisant les conditions initiales 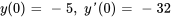 .
.
Afficher/Masquer la solution
a) Pour trouver le wronskien, il faut utiliser l’équation 3.1.3. Il faut d’abord trouver les dérivées premières des solutions  et
et  .
.

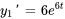
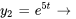
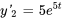
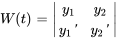

 pour tout instant
pour tout instant 
Le wronskien 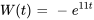 n’est jamais égal à zéro quelle que soit la valeur de
n’est jamais égal à zéro quelle que soit la valeur de , ce qui signifie que les solutions sont linéairement indépendantes sur l’intervalle
, ce qui signifie que les solutions sont linéairement indépendantes sur l’intervalle 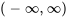 .
.
b) Comme les solutions sont linéairement indépendantes, on peut exprimer la solution générale de l’équation différentielle comme une combinaison de ces solutions.
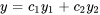
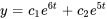
Ici, 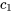 et
et 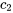 sont des constantes qui seront déterminées en fonction des conditions initiales ou des exigences spécifiques du problème.
sont des constantes qui seront déterminées en fonction des conditions initiales ou des exigences spécifiques du problème.
c) Il faut appliquer les conditions initiales pour trouver les constantes 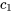 et
et 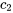 .
.
En appliquant la condition initiale à  :
:
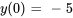

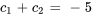
En appliquant la condition initiale à 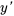 :
:
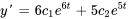
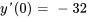
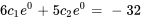
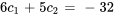
Pour déterminer 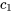 et
et 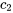 , il faut résoudre le système suivant de deux équations et deux inconnues :
, il faut résoudre le système suivant de deux équations et deux inconnues :
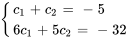
La résolution du système donne

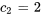
La solution du problème de valeur initiale est donc
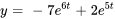
Prenons un exemple
Prenons un exemple
Section 3.1 Exercices
- Calcule le wronskien des fonctions
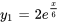 et
et 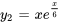 . Détermine si les fonctions sont linéairement indépendantes pour tous les nombres réels.
. Détermine si les fonctions sont linéairement indépendantes pour tous les nombres réels.
Afficher/Masquer la réponse
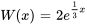 ; les fonctions sont linéairement indépendantes parce que
; les fonctions sont linéairement indépendantes parce que 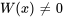 pour tous les nombres réels.
pour tous les nombres réels. - Deux solutions à l’équation
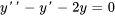 sont
sont 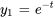 ,
, 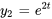 .
.
a) Trouve le wronskien.
b) Trouve la solution satisfaisant les conditions initiales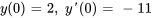 .
.
Afficher/Masquer la réponse
a)
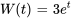
b)
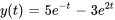
- Deux solutions à l’équation
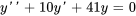 sont
sont 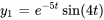 ,
, 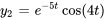 .
.
a) Trouve le wronskien.
b) Trouve la solution satisfaisant les conditions initiales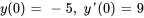 .
.
Afficher/Masquer la réponse
a)
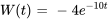
b)