2.5 Applications d’EDO du premier ordre
A. Introduction
La modélisation mathématique est le processus qui consiste à traduire des problèmes du monde réel en langage mathématique. Il s’agit de formuler, de développer et de tester rigoureusement des modèles pour représenter et résoudre des problèmes complexes. Les équations différentielles, qu’elles soient ordinaires ou partielles, jouent un rôle essentiel dans ces modèles. Elles relient une fonction à ses dérivées, qui représentent les taux de changement. Elles sont donc particulièrement adaptées à la modélisation de systèmes dynamiques pour lesquels il est essentiel de comprendre l’évolution des choses.
Dans cette section, nous allons voir comment les équations différentielles du premier ordre sont appliquées dans divers domaines, notamment les processus de croissance et de décroissance, le mélange de substances, la loi de refroidissement de Newton, la dynamique de la chute d’objets et l’analyse des circuits électriques.
B. Croissance et décroissance démographique
L’une des applications les plus courantes des équations différentielles du premier ordre est la modélisation de la croissance ou de la décroissance démographique. Les modèles permettent de comprendre comment les populations évoluent dans le temps en raison des naissances, des décès, de l’immigration et de l’émigration. Le modèle de croissance démographique le plus simple est le modèle de croissance exponentielle, qui suppose un environnement aux ressources illimitées. Il est représenté par l’équation différentielle suivante :
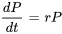
où 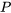 est la taille de la population, et
est la taille de la population, et 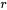 est la constante de proportionnalité. La solution de cette équation différentielle séparable est
est la constante de proportionnalité. La solution de cette équation différentielle séparable est
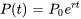
où 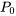 est la population initiale à l’instant
est la population initiale à l’instant 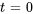 .
.
Si 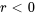 , la population décroît exponentiellement et si
, la population décroît exponentiellement et si 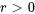 , la population croît exponentiellement. Ce modèle implique que la population croît continuellement et sans limites, ce qui n’est démographiquement guère réaliste à long terme compte tenu des limitations de ressources, d’espace, etc. Toutefois, il s’agit d’une bonne approximation pour les populations ne présentant pas de contraintes significatives en matière de ressources ou pour les prévisions à court terme.
, la population croît exponentiellement. Ce modèle implique que la population croît continuellement et sans limites, ce qui n’est démographiquement guère réaliste à long terme compte tenu des limitations de ressources, d’espace, etc. Toutefois, il s’agit d’une bonne approximation pour les populations ne présentant pas de contraintes significatives en matière de ressources ou pour les prévisions à court terme.
Lorsqu’il s’agit de problèmes où les taux d’entrée et de sortie de population d’une région sont différents, il est essentiel de comprendre que le taux global de variation de la population est le résultat de la différence entre le taux d’entrée de la population (immigrations ou naissances) et le taux de sortie de la population (émigrations ou décès). Ce taux peut être représenté sous la forme d’une équation différentielle qui modélise la variation nette de la population au fil du temps. L’approche générale consiste à établir une équation d’équilibre reflétant ces taux :
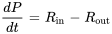
Ici, 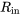 est le taux auquel la population entre dans la région et
est le taux auquel la population entre dans la région et 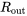 est le taux auquel la population quitte la région.
est le taux auquel la population quitte la région.
Une population de poissons dans un lac croît à un rythme proportionnel à sa taille actuelle. En l’absence de facteurs extérieurs, la population de poissons double en dix jours. Cependant, chaque jour, cinq poissons migrent dans la zone, seize sont capturés par les pêcheurs et sept meurent de causes naturelles. Déterminer si la population survivra au fil du temps et, si ce n’est pas le cas, quand elle s’éteindra. La population initiale est de 200 poissons.
Afficher/Masquer la solution
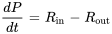
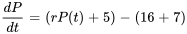
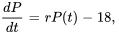
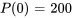
Avant de résoudre ce PVI, il faut trouver 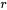 en utilisant l’information sur le doublement de la population en dix jours sans facteurs externes. Si la population initiale est de 200, alors elle atteindra 400 en deux jours.
en utilisant l’information sur le doublement de la population en dix jours sans facteurs externes. Si la population initiale est de 200, alors elle atteindra 400 en deux jours.
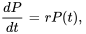
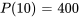
La solution générale de cette équation différentielle séparable est
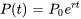
En appliquant la condition initiale, on obtient
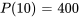
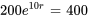
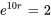
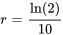
Maintenant, revenons à l’équation différentielle originale.
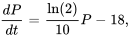
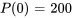
Il s’agit d’une équation différentielle linéaire, que nous écrivons sous forme standard :
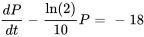
Le facteur intégrant est
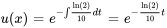
La solution générale est
![P(t)=e^((ln(2))/10 t) [int -18 e^(-(ln(2))/10 t) dt+C] P(t)=e^((ln(2))/10 t) [int -18 e^(-(ln(2))/10 t) dt+C]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/f55a70c813a5ab457392aba7ef43166d-2.png)
![P(t)=e^((ln(2))/10 t) [18(10/(ln(2)) )e^(-(ln(2))/10 t) +C] P(t)=e^((ln(2))/10 t) [18(10/(ln(2)) )e^(-(ln(2))/10 t) +C]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/285dc3c2660cdb2056d390829a6697f8-2.png)
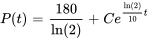
En appliquant la condition initiale, on obtient
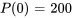
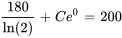
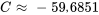
La solution spécifique est donc
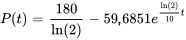
Le terme exponentiel a un exposant positif et croît donc de manière exponentielle. Cependant, comme le coefficient du terme exponentiel est négatif, l’ensemble de la population diminue et finit par disparaître. Pour déterminer quand la population finira par s’éteindre, il faut prendre 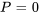 et trouver la valeur de
et trouver la valeur de  .
.
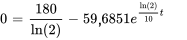
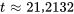 jours
jours
Prenons un exemple
C. Problèmes de mélanges
Les problèmes de mélanges consistent à combiner des substances ou des quantités et à observer leur interaction dans le temps. Il peut s’agir de polluants dans un lac, de différents produits chimiques dans un réacteur, voire de sucre se dissolvant dans du café. L’élément commun à ces scénarios est le changement de concentration des substances dans un mélange au fil du temps. Les équations différentielles, en particulier celles du premier ordre, permettent de modéliser et de résoudre ces situations dynamiques.
Dans les problèmes de mélanges, 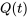 représente la quantité de substance dissoute dans le fluide, qui évolue avec le temps au débit (
représente la quantité de substance dissoute dans le fluide, qui évolue avec le temps au débit (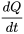 ). Le débit est influencé par les entrées et sorties de la substance.
). Le débit est influencé par les entrées et sorties de la substance.
Pour un problème de mélanges type, on peut avoir un réservoir contenant une certaine quantité de fluide dans lequel une autre substance est mélangée. La concentration de la substance dans le réservoir change au fur et à mesure que l’on ajoute ou que l’on retire de la substance. L’équation différentielle générale du premier ordre pour un tel scénario est similaire à celle que nous avons examinée pour l’évolution démographique d’une région.

Ici,  est le taux auquel la substance entre dans le système et
est le taux auquel la substance entre dans le système et  est le taux auquel la substance quitte le système.
est le taux auquel la substance quitte le système.
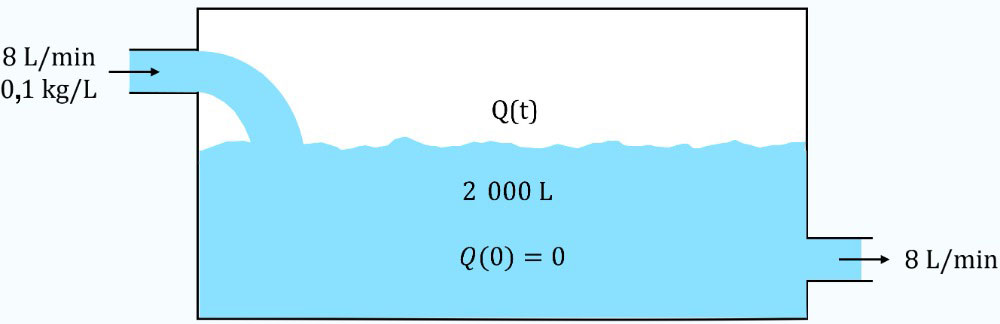
Prenons une citerne renfermant 2 000 litres d’eau fraîche. En commençant à l’instant 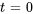 , l’eau contenant 0,1 kilogramme de sel par litre est versée dans la citerne au taux de
, l’eau contenant 0,1 kilogramme de sel par litre est versée dans la citerne au taux de 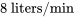 . Le mélange est maintenu uniforme par agitation et est évacué de la citerne au même rythme qu’il est rempli. a) Formule une équation différentielle pour la quantité de sel dans la citerne (
. Le mélange est maintenu uniforme par agitation et est évacué de la citerne au même rythme qu’il est rempli. a) Formule une équation différentielle pour la quantité de sel dans la citerne (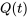 ) à n’importe quel instant et résous l’équation pour déterminer
) à n’importe quel instant et résous l’équation pour déterminer 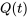 . b) Déterminer quand la concentration de sel dans la citerne va atteindre
. b) Déterminer quand la concentration de sel dans la citerne va atteindre 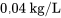 .
.
Afficher/Masquer la solution
Informations données
- Le volume d’eau dans la citerne (
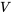 ) est constant puisque les entrées et sorties d’eau sont égales :
) est constant puisque les entrées et sorties d’eau sont égales : 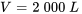
- Débit d’entrée d’eau
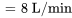
- Débit de sortie d’eau
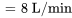
- Concentration de sel entrant :
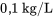
a) Notre tâche consiste à déterminer le taux auquel le sel entre dans la citerne ( ) et le taux auquel il quitte la citerne. Il ne faut pas oublier que le taux auquel l’eau entre dans la citerne est différent du taux auquel le sel pénètre et quitte la citerne.
) et le taux auquel il quitte la citerne. Il ne faut pas oublier que le taux auquel l’eau entre dans la citerne est différent du taux auquel le sel pénètre et quitte la citerne.

Le taux auquel le sel entre dans la citerne est le produit de la concentration de sel de l’eau entrante et le débit d’entrée de l’eau :
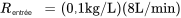
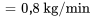
Le taux auquel le sel quitte la citerne est la concentration de sel dans la citerne (rapport entre le sel dans la citerne et le volume d’eau dans la citerne), multipliée par le débit de sortie de l’eau. À tout moment, la quantité de sel dans la citerne est 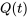 .
.
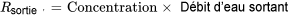
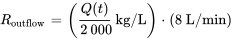
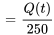
Au départ, la citerne ne contient que de l’eau pure non salée, de sorte que 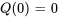 . Ainsi, l’équation différentielle avec une condition initiale devient
. Ainsi, l’équation différentielle avec une condition initiale devient

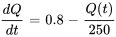 ,
, 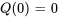
L’équation différentielle est séparable (et linéaire) et peut donc être facilement résolue. La solution du PVI est
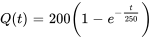
Cette équation nous donne le volume de sel dans la citerne 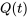 en kilogrammes à tout instant t après le début du processus.
en kilogrammes à tout instant t après le début du processus.
b) Pour déterminer quand la concentration de sel dans la citerne atteint 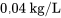 , il faut d’abord trouver une équation pour la concentration en termes de temps. La concentration est le rapport entre la quantité de sel et le volume d’eau. Le volume reste constant à 2 000 litres. Ainsi, la concentration
, il faut d’abord trouver une équation pour la concentration en termes de temps. La concentration est le rapport entre la quantité de sel et le volume d’eau. Le volume reste constant à 2 000 litres. Ainsi, la concentration 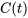 à l’instant t est la quantité de sel divisée par le volume total
à l’instant t est la quantité de sel divisée par le volume total 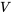 :
:
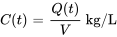
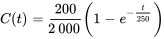
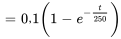
Maintenant, il faut trouver la valeur de t quand 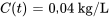 .
.
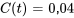
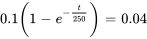
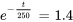
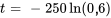
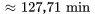
La concentration de sel dans la citerne atteindra 0,04 kg/L environ 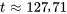 minutes après le début du processus.
minutes après le début du processus.
Prenons un exemple
D. Loi de refroidissement de Newton
La loi de refroidissement de Newton décrit la vitesse à laquelle la température d’un objet change lorsqu’il est exposé à un environnement dont la température est différente et constante. Le principe fondamental est que le taux de variation de température (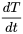 ) est proportionnel à la différence entre la température de l’objet (
) est proportionnel à la différence entre la température de l’objet (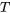 ) et la température ambiante (
) et la température ambiante (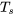 ). L’équation différentielle représentant la loi de refroidissement de Newton est donc
). L’équation différentielle représentant la loi de refroidissement de Newton est donc
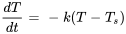
Dans cette équation, 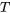 représente la température de l’objet à n’importe quel instant
représente la température de l’objet à n’importe quel instant  ,
, 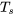 est la température ambiante constante,
est la température ambiante constante, 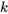 est une constante positive dépendante des caractéristiques de l’objet et de son milieu environnant et
est une constante positive dépendante des caractéristiques de l’objet et de son milieu environnant et 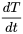 est le taux de variation de la température. Lorsque la température initiale est dénotée par
est le taux de variation de la température. Lorsque la température initiale est dénotée par 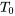 , le problème de valeur initiale est
, le problème de valeur initiale est
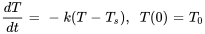
Cette équation différentielle est séparable (et linéaire), et a pour solution
Le signe négatif de l’exposant indique que la différence de température entre l’objet et son milieu environnant diminue exponentiellement avec le temps. Cette formule est valable même si l’objet est initialement plus chaud ou plus froid que son milieu environnant, décrivant à la fois les processus de refroidissement et de réchauffement selon les hypothèses de la loi.
Prenons un microprocesseur fonctionnant dans un environnement dans lequel la température ambiante est constante à 25 ◦C. Après une longue période de fonctionnement, la température du microprocesseur est de 75 ◦C. Une fois l’appareil éteint, le microprocesseur commence à refroidir jusqu’à atteindre la température ambiante. Supposons que la constante de refroidissement caractéristique pour ce scénario, qui dépend des propriétés de transfert de chaleur du microprocesseur et de son système de refroidissement, est de 0,07/min. a) Trouver l’équation de la température du microprocesseur. b) Quelle sera la température du microprocesseur dix minutes après l’arrêt de l’appareil? c) Combien de temps faudra-t-il pour que le microprocesseur refroidisse à 35 ◦C?
pour ce scénario, qui dépend des propriétés de transfert de chaleur du microprocesseur et de son système de refroidissement, est de 0,07/min. a) Trouver l’équation de la température du microprocesseur. b) Quelle sera la température du microprocesseur dix minutes après l’arrêt de l’appareil? c) Combien de temps faudra-t-il pour que le microprocesseur refroidisse à 35 ◦C?
Afficher/Masquer la solution
Informations données :
- Température ambiante :
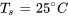
- Température initiale du microprocesseur :
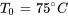
- Constante de refroidissement t:
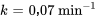
a) En introduisant les valeurs données dans la solution de l’équation de la loi de refroidissement de Newton, l’équation de la section 2.5.1, on obtient la formule pour 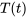 .
.
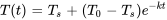
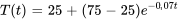
b) Pour trouver la température du microprocesseur dix minutes après l’arrêt de l’appareil, il faut introduire 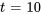 minutes dans
minutes dans 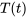 .
.
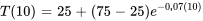
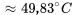
c) Pour trouver quand la température sera de 35 ◦C, il faut réarranger la formule quand 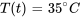 .
.
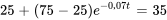
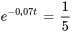
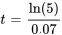
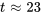 minutes
minutes
Il faut 23 minutes au microprocesseur pour refroidir à 35 ◦C.
Prenons un exemple
E. Dynamique de la chute d’objets
La dynamique de la chute d’objets est un exemple classique de la façon dont les équations différentielles modélisent des situations du monde réel. Ce phénomène est directement lié à la deuxième loi du mouvement de Newton, qui stipule que la force agissant sur un objet est égale à la masse de l’objet multipliée par son accélération.
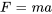
Dans cette équation, la force peut dépendre du temps ( ), du déplacement (
), du déplacement ( ) et de la vitesse (
) et de la vitesse (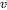 ). Pour ce qui est des équations du premier ordre, nous considérons généralement des problèmes où
). Pour ce qui est des équations du premier ordre, nous considérons généralement des problèmes où 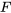 ne dépend pas de
ne dépend pas de  , car l’inclusion conduit souvent à des équations d’ordre supérieur. Étant donné que l’accélération de l’objet (
, car l’inclusion conduit souvent à des équations d’ordre supérieur. Étant donné que l’accélération de l’objet (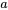 ) est
) est 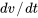 , l’équation de la deuxième loi du mouvement de Newton devient
, l’équation de la deuxième loi du mouvement de Newton devient
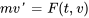 .
.
La résolution de cette équation permet d’obtenir 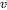 en fonction du temps.
en fonction du temps.
Modèle de base
Le modèle le plus simple de chute d’un objet applique la deuxième loi de Newton en considérant la pesanteur comme la seule force agissant sur l’objet. Ici, la force due à la pesanteur est, ce qui donne l’équation différentielle
où est l’accélération due à la pesanteur, la masse étant supposée constante. Ce modèle part du principe qu’il n’y a pas de résistance de l’air et que le champ gravitationnel est uniforme. La valeur approximative de 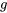 est
est 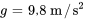 (unité métrique) ou
(unité métrique) ou 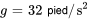 (unité britannique). Le signe de
(unité britannique). Le signe de 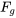 change en fonction de la convention de direction que l’on définit pour un problème. Par exemple, si l’on décide que la direction ascendante est positive, puisque la force due à la pesanteur est descendante, l’équation est simplifiée comme suit :
change en fonction de la convention de direction que l’on définit pour un problème. Par exemple, si l’on décide que la direction ascendante est positive, puisque la force due à la pesanteur est descendante, l’équation est simplifiée comme suit :
Inclusion de la résistance de l’air
En réalité, lorsqu’un objet tombe, il rencontre la résistance de l’air, qui s’oppose au mouvement de l’objet. La force nette exercée sur l’objet devient alors une combinaison de la pesanteur et de la résistance de l’air, ce qui modifie l’équation en
où 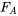 est la force de la résistance de l’air.
est la force de la résistance de l’air.
La force de la résistance de l’air est souvent proportionnelle à la vitesse de l’objet, de sorte que 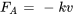 , où
, où 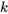 est une constante de proportionnalité (valeur positive) qui représente le coefficient de la résistance de l’air. Lorsque l’on résout des problèmes impliquant des forces et des mouvements, il est important de veiller à ce que les conventions relatives aux directions positives et négatives soient cohérentes.
est une constante de proportionnalité (valeur positive) qui représente le coefficient de la résistance de l’air. Lorsque l’on résout des problèmes impliquant des forces et des mouvements, il est important de veiller à ce que les conventions relatives aux directions positives et négatives soient cohérentes.
Au fur et à mesure que l’objet tombe, la résistance de l’air augmente avec la vitesse jusqu’à ce qu’elle équilibre la force gravitationnelle. À ce point d’équilibre, la force nette est nulle et l’objet n’accélère plus, atteignant une vitesse constante, appelée vitesse limite de chute.
Prenons un objet ayant une masse de 25 kg et se déplaçant initialement vers le bas à une vitesse de -29 m/s. En chutant, l’objet traverse l’atmosphère, qui exerce une force de résistance à son mouvement. La force de résistance est proportionnelle à la vitesse de l’objet. Plus précisément, lorsque la vitesse de l’objet est de 2 m/s, on sait que la force de résistance est de 20 N. a) Écris l’équation différentielle décrivant le mouvement de l’objet en termes de vitesse et de temps. b) Résous l’équation différentielle pour trouver la vitesse de l’objet en fonction du temps, 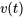 . c) Détermine la vitesse limite de chute de l’objet.
. c) Détermine la vitesse limite de chute de l’objet.
Afficher/Masquer la solution
Informations données
- Masse de l’objet :
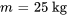
- Vitesse initiale :
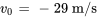
- Accélération due à la pesanteur :
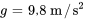
a) La vitesse descendante est exprimée par une valeur négative. Par conséquent, la direction ascendante est positive et la direction descendante est négative.
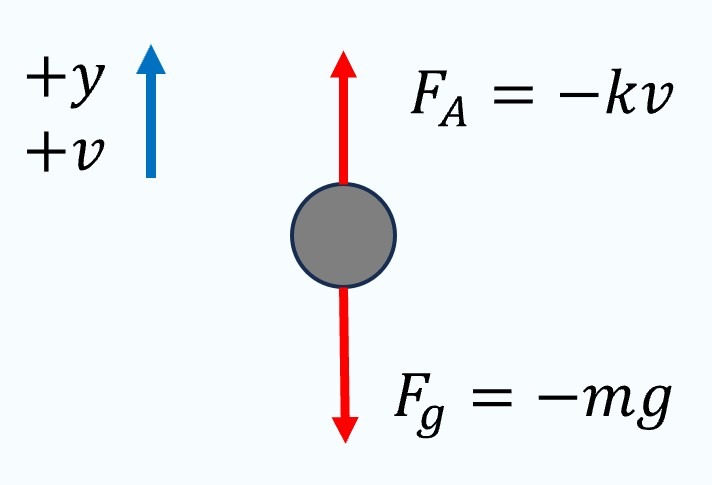
Les deux principales forces agissant sur l’objet sont la pesanteur et la résistance de l’air. La force de pesanteur agit toujours vers le bas, que nous considérons comme une valeur négative dans notre système de coordonnées, et est donnée par 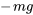 .
.
D’autre part, la résistance de l’air agit dans la direction opposée au mouvement de l’objet, en produisant une force ascendante lorsque l’objet chute. Cette force est représentée par 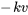 . Le signe négatif dans
. Le signe négatif dans 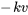 garantit que la force de la résistance de l’air est toujours opposée au mouvement : elle est positive (ascendante) lorsque l’objet chute (
garantit que la force de la résistance de l’air est toujours opposée au mouvement : elle est positive (ascendante) lorsque l’objet chute ( 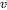 est négatif) et négative (descendante) lorsque l’objet se déplace vers le haut (
est négatif) et négative (descendante) lorsque l’objet se déplace vers le haut (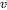 est positif).
est positif).
En combinant ces forces, l’équation du mouvement est
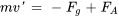
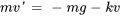
Nous pouvons utiliser l’information selon laquelle l’ampleur de la résistance de l’air est de 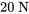 lorsque la vitesse est
lorsque la vitesse est 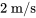 pour trouver
pour trouver 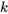 :
:
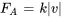
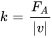
k=20/2=10 kg/s
En introduisant les valeurs avec la condition initiale  , on obtient le PVI
, on obtient le PVI
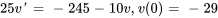
b) Il s’agit d’une équation différentielle séparable (et linéaire). La solution générale de l’équation est
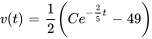
En appliquant la condition initiale, on obtient
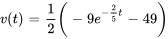
c) La vitesse limite de chute est
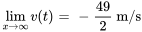
Prenons un exemple
F. Circuits électriques : RL et RC
Les circuits électriques font partie intégrante des avancées technologiques et fonctionnent grâce à l’interaction de composants tels que des résistances, des inducteurs et des condensateurs. Dans cette section, nous abordons spécifiquement l’application des équations différentielles du premier ordre pour analyser les circuits électriques composés d’une source de tension avec soit une résistance et un inducteur (RL), soit une résistance et un condensateur (RC), comme illustré à la figure 2.5.1 Les circuits contenant à la fois un inducteur et un condensateur, connus sous le nom de circuits RLC, sont régis par des équations différentielles du second ordre, un sujet sur lequel nous reviendrons dans le chapitre suivant.
(a) (b)
(b) 
Figure 2.5.1 (a) Circuit série RL et (b) Circuit série RC
Les lois de Kirchhoff – lois des nœuds et loi des mailles – constituent les principes fondamentaux régissant les circuits électriques. La loi des nœuds de Kirchhoff stipule que le courant total entrant en un point (nœud) doit être égal au courant total sortant, ce qui implique que la somme algébrique des courants dans un nœud est nulle. La loi des mailles Kirchhoff stipule que la somme algébrique de toutes les tensions autour d’une boucle fermée d’un circuit (maille) doit être égale à zéro.
La loi des nœuds de Kirchhoff implique que le même courant passe à travers tous les éléments des circuits de la figure 2.5.1. Pour appliquer la loi des mailles de Kirchhoff, il est essentiel de comprendre la baisse de tension à travers chaque composant :
a) Selon la loi d’Ohm, la baisse de tension 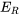 aux bornes d’une résistance est proportionnelle au courant I circulant entre ces bornes, ce qui s’exprime par
aux bornes d’une résistance est proportionnelle au courant I circulant entre ces bornes, ce qui s’exprime par 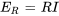 , où
, où 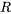 est la résistance.
est la résistance.
b) Selon la loi de Faraday, complétée par la loi de Lenz, la baisse de tension 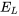 aux bornes d’un inducteur est proportionnelle au taux de variation du courant, ce qui s’exprime par
aux bornes d’un inducteur est proportionnelle au taux de variation du courant, ce qui s’exprime par 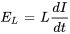 , où
, où 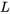 est l’inductance.
est l’inductance.
c) La baisse de tension 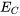 aux bornes d’un condensateur est proportionnelle à la charge électrique q qui y est stockée, ce qui est représenté par
aux bornes d’un condensateur est proportionnelle à la charge électrique q qui y est stockée, ce qui est représenté par 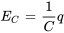 ,
, 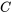 étant la capacité.
étant la capacité.
Modèle de circuit RL
Dans cette section, nous dérivons le modèle mathématique d’un circuit RL tel qu’illustré à la figure 2.5.1, la dérivation du modèle pour un circuit RC étant réservée aux exercices. Considérons que 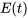 est la source de tension du circuit RL. En appliquant la loi des mailles de Kirchhoff, nous avons
est la source de tension du circuit RL. En appliquant la loi des mailles de Kirchhoff, nous avons
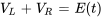
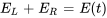
où 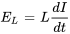 est la tension aux bornes de l’inducteur et
est la tension aux bornes de l’inducteur et 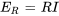 est la tension aux bornes de la résistance. En substituant ces éléments dans l’équation, on obtient une équation différentielle linéaire du premier ordre
est la tension aux bornes de la résistance. En substituant ces éléments dans l’équation, on obtient une équation différentielle linéaire du premier ordre
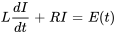
ou, dans la forme standard
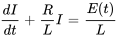
Pour résoudre cette équation différentielle linéaire, il faut utiliser un facteur intégrant
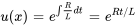
la solution générale pour le courant 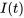 est donc :
est donc :
Avec un 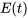 spécifique et une condition initiale, telle que
spécifique et une condition initiale, telle que 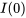 , on peut déterminer le courant I(t) avec l’équation ci-dessus. Une fois que
, on peut déterminer le courant I(t) avec l’équation ci-dessus. Une fois que 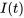 est connu, la tension aux bornes de la résistance et de l’inducteur peut être déterminée.
est connu, la tension aux bornes de la résistance et de l’inducteur peut être déterminée.
Prenons un circuit série RL avec une résistance de 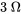 et un inducteur de
et un inducteur de 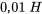 , alimenté par une source de tension de
, alimenté par une source de tension de 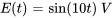 . Au départ, le courant aux bornes de la résistance,
. Au départ, le courant aux bornes de la résistance, 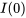 , est de 0 A. Calcule ce qui suit : a) le courant
, est de 0 A. Calcule ce qui suit : a) le courant 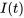 dans le circuit en fonction du temps, b) la tension aux bornes de l’inducteur en fonction du temps et c) la tension aux bornes de la résistance en fonction du temps.
dans le circuit en fonction du temps, b) la tension aux bornes de l’inducteur en fonction du temps et c) la tension aux bornes de la résistance en fonction du temps.
Afficher/Masquer la solution
Informations données :
- Résistance :
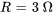
- Inducteur :
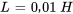
- Source de tension :
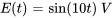
- Condition initiale :
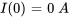
a) Trouver le courant 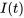
L’équation différentielle pour un circuit série RL selon la loi des mailles de Kirchhoff est
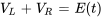
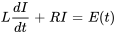
En introduisant les valeurs données, on obtient
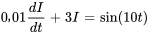
Il s’agit d’une équation différentielle linéaire non homogène du premier ordre.
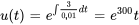
L’équation de la section 2.5.3 donne la solution de cette équation différentielle.
![I(t)=e^(-300t)[100int e^(300t) \ sin(10t) dt +C] I(t)=e^(-300t)[100int e^(300t) \ sin(10t) dt +C]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/c3eb18471d8917c7a4c4383be9526667-2.png)
Le côté droit implique une intégrale avec des termes exponentiels et sinusoïdaux qui est généralement résolue en utilisant l’intégration par parties. Nous ne fournissons que la solution finale de l’intégrale, les étapes détaillées de l’intégration faisant l’objet d’un autre un exercice à explorer plus avant.
![I(t)=e^(-300t)[-10/901e^(300t)cos(10t)+300/901e^(300t)sin(10t)+C] I(t)=e^(-300t)[-10/901e^(300t)cos(10t)+300/901e^(300t)sin(10t)+C]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/e2b42a7bdcd88459a2f463df564dbf72-2.png)
Ce qui peut être simplifié en
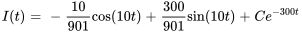
En appliquant la condition initiale, on obtient
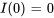
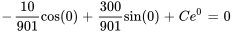
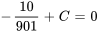
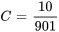
Le courant est donc
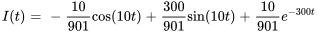
b) Trouver la tension aux bornes de l’inducteur 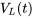
Pour trouver la tension aux bornes de l’inducteur, il faut d’abord différencier 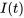 .
.
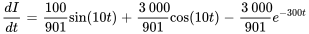
La tension aux bornes de l’inducteur est donc
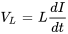
![V_L(t)=0.01[100/901sin(10t)+3000/901cos(10t)-3000/901e^(-300t) ] V_L(t)=0.01[100/901sin(10t)+3000/901cos(10t)-3000/901e^(-300t) ]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/f675842c935345f068e4f9764e8e3140-2.png)
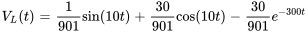
c) Trouver la tension aux bornes de la résistance 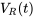
De façon similaire, la tension aux bornes de la résistance est obtenue par
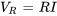
![V_R(t)=3[-10/901cos(10t)+300/901sin(10t)+10/901e^(-300t) ] V_R(t)=3[-10/901cos(10t)+300/901sin(10t)+10/901e^(-300t) ]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/08e66f064b10ed8d859f659eaf6b3f41-2.png)
Prenons un exemple
Section 2.5 Exercices
- Une cuve contient initialement une solution de 11 kg de sel dans 2 400 litres d’eau. De l’eau contenant 0,2 kg de sel par litre est ajoutée à la cuve à un débit de 11 L/min, et la solution résultante est évacuée à la même vitesse. Disons que
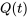 indique la quantité (kg) de sel à l’instant
indique la quantité (kg) de sel à l’instant  (min). a) Rédige une équation différentielle pour
(min). a) Rédige une équation différentielle pour 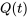 . b) Trouve la quantité
. b) Trouve la quantité 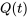 de sel dans la cuve à l’instant
de sel dans la cuve à l’instant  . c) Détermine quand la concentration de sel dans la cuve atteindra 0,1 kg/L. Arrondis le résultat à la minute la plus proche.
. c) Détermine quand la concentration de sel dans la cuve atteindra 0,1 kg/L. Arrondis le résultat à la minute la plus proche.
Afficher/Masquer la réponse
a)
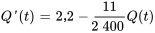
b)
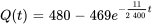
c) 146 min
- Un fluide initialement à 135 ◦C est placé dehors, un jour où la température est de -30 ◦C, et la température du fluide chute de 30 ◦C en une minute. Disons que
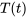 est la température, en degrés Celsius, à l’instant
est la température, en degrés Celsius, à l’instant  , en minutes. (a) Trouve la température
, en minutes. (a) Trouve la température 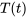 du fluide pour
du fluide pour 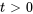 . (b) Trouve la température du fluide quinze minutes après qu’il a été placé dehors. Arrondis votre résultat à deux décimales.
. (b) Trouve la température du fluide quinze minutes après qu’il a été placé dehors. Arrondis votre résultat à deux décimales.
Afficher/Masquer la réponse
a)
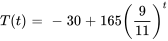
b)

- Un objet d’une masse de
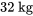 a une vitesse descendante initiale de
a une vitesse descendante initiale de 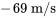 . Supposons que l’atmosphère exerce une force de résistance proportionnelle à la vitesse. La résistance est de
. Supposons que l’atmosphère exerce une force de résistance proportionnelle à la vitesse. La résistance est de 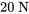 lorsque que la vitesse est de
lorsque que la vitesse est de 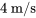 . Utilise
. Utilise 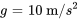 . a) Rédige une équation différentielle en termes de vitesse
. a) Rédige une équation différentielle en termes de vitesse 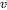 et d’accélération
et d’accélération 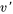 . b) Trouve la vitesse
. b) Trouve la vitesse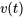 de l’objet.
de l’objet.
Afficher/Masquer la réponse
a)
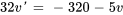
b)
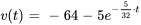
- Supposons qu’un circuit RL avec une résistance de
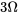 et un inducteur de
et un inducteur de 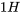 est alimenté par une tension de
est alimenté par une tension de 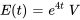 . Si la résistance initiale est
. Si la résistance initiale est 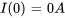 , trouve le courant
, trouve le courant 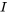 et la tension aux bornes de l’inducteur
et la tension aux bornes de l’inducteur 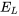 et de la résistance
et de la résistance 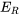 en termes de temps
en termes de temps  . Trouve le courant
. Trouve le courant 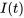 .
.
Afficher/Masquer la réponse
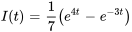

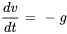
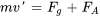
![I(t)=e^(-Rt//L)[int e^(Rt//L) \ (E(t))/L dt +C] I(t)=e^(-Rt//L)[int e^(Rt//L) \ (E(t))/L dt +C]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/c9c2004d7046726022c4099db379bef9-2.png)