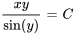2.4 Facteurs intégrants
Face à une équation différentielle du premier ordre non exacte, la méthode des facteurs intégrants fournit un moyen systématique de la transformer en une équation exacte qui peut être résolue. Cette section explore les techniques d’utilisation des facteurs intégrants pour résoudre les équations différentielles.
Parfois, une équation différentielle qui n’est pas exacte au départ peut être transformée en une équation exacte en la multipliant par une fonction appropriée,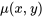 
. Prenons l’équation
.
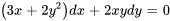Elle n’est pas exacte parce que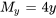 
et 
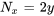ne correspondent pas. Or, si on multiplie l’équation tout entière par une fonction 
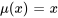, elle devient
.
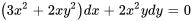Cette équation est maintenant exacte, puisque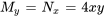 
. Cette équation modifiée peut alors être résolue par les méthodes d’équation exacte évoquées à la section 2.3.
La fonction 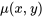est un facteur intégrant pour l’équation si, lorsqu’elle est multipliée par l’équation, elle donne une équation exacte. En termes formels, si la multiplication de l’équation différentielle par 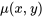, comme dans
,
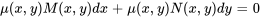la rend exacte, alors 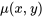est le facteur intégrant.
Méthode pour trouver le facteur intégrant spécial
Lorsque vous tombez sur une équation différentielle du premier ordre sous la forme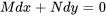 
qui n’est ni séparable, ni linéaire, vous pouvez tout de même la résoudre en trouvant un facteur intégrant spécial. Suivre ces étapes :
1. Calculer les dérivées partielles : Calculer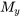 
et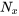 
.
2. Tester l’exactitude :
- Si
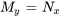, alors l’équation est déjà exacte, aucun facteur intégrant n’est nécessaire. - Si
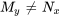, l’équation n’est pas exacte, il faut trouver un facteur intégrant.
3. Trouver un facteur intégrant spécial :
- Calculer l’expression
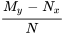(i). Si (i) est une fonction de 
uniquement, alors un facteur intégrant est donné par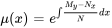 
. - Si (i) n’est pas une fonction de uniquement, calculer l’expression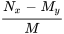
(ii). Si (ii) est une fonction de 
uniquement, alors un facteur intégrant est donné par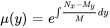 
.
4. Appliquer le facteur intégrant : Multiplier l’équation tout entière par le facteur intégrant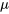 
de façon à la transformer en équation exacte.
5. Résoudre l’équation exacte : Une fois que l’équation est exacte, il faut la résoudre au moyen de la méthode présentée à la section 2.3 pour les équations exactes.
Résoudre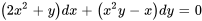 
Afficher/Masquer la solution
Un rapide contrôle montre que l’équation n’est ni séparable, ni linéaire, ni exacte. Il faut donc vérifier s’il existe un facteur intégrant spécial :
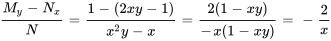
Puisque (i) est la fonction de uniquement, un facteur intégrant est donné par
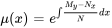
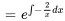
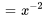
En multipliant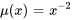 
par l’équation différentielle originale, on obtient l’équation exacte
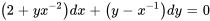
En résolvant l’équation par la méthode exacte, on obtient la solution implicite
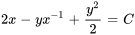
Prenons un exemple
Section 2.4 Exercices
- Trouve un facteur intégrant pour l’équation suivante :
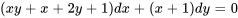
Afficher/Masquer la réponse
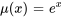
- Pour l’équation différentielle donnée, a) détermine le facteur intégrant et b) trouve une solution générale.
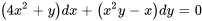
Afficher/Masquer la réponse
a)
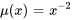
b)
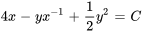
- Résous l’équation différentielle :
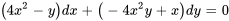
Afficher/Masquer la réponse
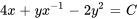
- Pour l’équation différentielle donnée, a) détermine le facteur intégrant et b) trouve une solution générale.
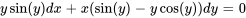
Afficher/Masquer la réponse
a)
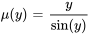
b)
