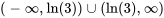2.3 Équations différentielles exactes
A. Introduction
Les équations différentielles exactes sont une catégorie d’équations différentielles du premier ordre qui peuvent être résolues avec une condition d’intégrabilité particulière. Cette section aborde les thèmes suivants : ce qui fait qu’une équation est exacte, comment vérifier cette condition et la méthodologie de résolution de ces équations.
Pour commencer, nous présentons un théorème fondamental, suivi d’un exemple illustrant son application. Ensuite, nous approfondissons le concept d’équations exactes et explorons une méthode pour les résoudre.
Théorème : si la fonction 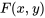 a des dérivées partielles continues
a des dérivées partielles continues 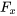 et
et 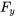 , alors l’équation
, alors l’équation 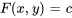 est une solution implicite à l’équation différentielle
est une solution implicite à l’équation différentielle 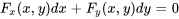 .
.
Ce théorème peut être prouvé en utilisant la différenciation implicite.
Montrer que 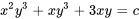 est une solution implicite à l’équation différentielle donnée.
est une solution implicite à l’équation différentielle donnée.
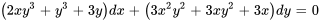
Afficher/Masquer la solution
Pour appliquer efficacement le théorème, il faut définir 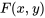 comme la fonction donnée dans la solution. Ensuite, il faut montrer que les termes multipliés par dx et dy sont, respectivement, les dérivées partielles
comme la fonction donnée dans la solution. Ensuite, il faut montrer que les termes multipliés par dx et dy sont, respectivement, les dérivées partielles 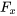 et
et 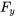 de
de 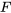 par rapport à
par rapport à  et
et  . Ce processus consiste à trouver ces dérivées partielles et à confirmer qu’elles correspondent aux termes respectifs de l’équation différentielle donnée.
. Ce processus consiste à trouver ces dérivées partielles et à confirmer qu’elles correspondent aux termes respectifs de l’équation différentielle donnée.
En laissant 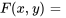
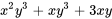 , on obtient ses dérivées partielles :
, on obtient ses dérivées partielles :
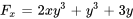
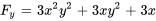
Nous observons que 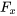 et
et 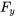 sont équivalents aux expressions multipliées par
sont équivalents aux expressions multipliées par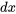 et
et 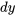 dans l’équation, respectivement, ce qui confirme que
dans l’équation, respectivement, ce qui confirme que 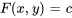 est la solution à l’équation différentielle donnée.
est la solution à l’équation différentielle donnée.
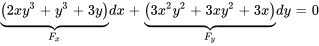
B. Solution d’équations exactes
Nous allons maintenant nous concentrer sur une compréhension plus large des équations différentielles exactes. Considérons une équation différentielle exprimée sous la forme
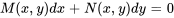
qui peut aussi être représentée sous la forme
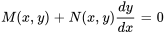 .
.
Une équation de cette forme est dite exacte s’il y a une fonction 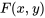 telle que ses dérivées partielles
telle que ses dérivées partielles 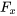 et
et 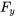 correspondent à
correspondent à 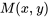 et
et 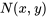 , respectivement. En l’absence d’une telle fonction
, respectivement. En l’absence d’une telle fonction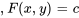 représente une solution à l’équation différentielle.
représente une solution à l’équation différentielle.
Par exemple, les équations 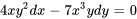 et
et 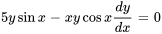 sont des exemples d’équations de forme exacte.
sont des exemples d’équations de forme exacte.
Les questions à se poser maintenant sont donc les suivantes :
- Comment déterminer si une équation différentielle donnée est exacte?
- Si elle est exacte, comment trouver la fonction
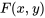 et, par conséquent, une solution?
et, par conséquent, une solution?
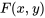 avec des dérivées partielles
avec des dérivées partielles 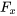 et
et 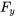 qui correspondent à
qui correspondent à 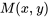 et
et 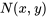 , respectivement. Si
, respectivement. Si 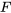 et ses dérivées partielles
et ses dérivées partielles 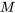 et
et 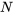 sont continues, alors les dérivées partielles secondes de
sont continues, alors les dérivées partielles secondes de 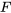 doivent être égales à :
doivent être égales à : 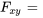
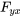
ou, de manière équivalente,
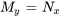
Cette relation est résumée dans le théorème ci-dessous.
1) Test d’exactitude
Théorème. Supposons que les dérivées premières de 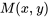 et
et 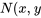
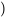 sont continues dans une région rectangulaire
sont continues dans une région rectangulaire 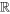 . L’équation différentielle
. L’équation différentielle
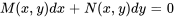
est donc exacte dans 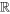 si et uniquement si la condition suivante est satisfaite pour tous les
si et uniquement si la condition suivante est satisfaite pour tous les 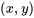 dans
dans 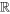 :
:
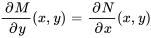
Pour ce qui est de la seconde question sur la résolution d’une équation différentielle exacte, il faut suivre la procédure ci-dessous.
2) Méthode de résolution d’équations exactes
1*. Trouver 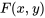 : si l’équation est exacte, alors
: si l’équation est exacte, alors 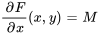 . Intégrer cette équation par rapport à
. Intégrer cette équation par rapport à  pour trouver une partie de
pour trouver une partie de 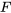 . Il ne faut pas oublier d’inclure une fonction arbitraire de l’autre variable, en l’occurrence
. Il ne faut pas oublier d’inclure une fonction arbitraire de l’autre variable, en l’occurrence  .
.
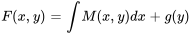
2. Déterminer la fonction arbitraire :
a. Pour trouver 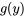 ,il faut d’abord déterminer
,il faut d’abord déterminer 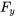 à partir de l’expression obtenue pour F(x,y) à l’étape 1. Comme
à partir de l’expression obtenue pour F(x,y) à l’étape 1. Comme 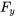 doit être égal à
doit être égal à 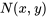 à partir de l’équation différentielle exacte, il faut définir
à partir de l’équation différentielle exacte, il faut définir 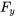 comme étant égal à
comme étant égal à 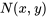 et trouver la valeur de
et trouver la valeur de 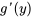 .
.
b. Après avoir isolé 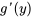 , il faut l’intégrer par rapport à
, il faut l’intégrer par rapport à  pour obtenir
pour obtenir 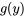 . Définir la constante d’intégration sur zéro. Remplacer le
. Définir la constante d’intégration sur zéro. Remplacer le 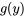 déterminé dans l’expression de
déterminé dans l’expression de 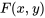 afin de terminer.
afin de terminer.
3. Formuler la solution générale : La solution de 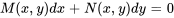 est donnée implicitement (sans solution pour
est donnée implicitement (sans solution pour  ) par
) par
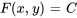
où 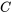 est une constante. L’équation représente la famille de courbes qui sont des solutions de l’équation différentielle.
est une constante. L’équation représente la famille de courbes qui sont des solutions de l’équation différentielle.
*Remarque : à titre d’alternative, on peut aussi commencer par intégrer 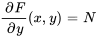 par rapport à
par rapport à  , puis suivre les mêmes étapes pour trouver
, puis suivre les mêmes étapes pour trouver 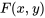 si l’intégration semble plus facile.
si l’intégration semble plus facile.
Déterminer si l’équation est exacte et, si tel est le cas, trouve la solution : 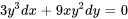
Afficher/Masquer la solution
1) Test d’exactitude :
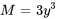

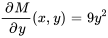
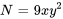

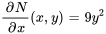
Comme 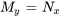 , l’équation est exacte.
, l’équation est exacte.
2) Trouver la solution :
1. Nous savons que 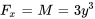 . Nous intégrons par rapport à
. Nous intégrons par rapport à  :
:
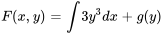
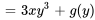
2a. Pour trouver 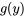 , il faut prendre la dérivée partielle de
, il faut prendre la dérivée partielle de 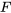 ci-dessus par rapport à
ci-dessus par rapport à  :
:
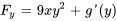
Comme 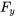 doit être égal à
doit être égal à 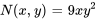 à partir de l’équation différentielle exacte, il faut définir
à partir de l’équation différentielle exacte, il faut définir 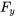 comme étant égal à
comme étant égal à 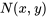 trouver la valeur de
trouver la valeur de 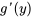 ou le déterminer par comparaison.
ou le déterminer par comparaison.
En comparant, nous déterminons que 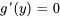 .
.
2b. En intégrant 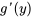 par rapport à y, on obtient
par rapport à y, on obtient 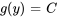 . En définissant la constante d’intégration sur zéro, on obtient
. En définissant la constante d’intégration sur zéro, on obtient 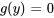 , soit
, soit 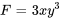 .
.
3. Ainsi, l’équation différentielle a pour solution implicite
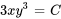
Prenons un exemple
Prenons un exemple
a) Résous le problème de valeur initiale et trouver la solution explicite 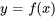 . b) Déterminer l’intervalle de validité.
. b) Déterminer l’intervalle de validité.
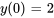
Afficher/Masquer la solution
a)
1) Test d’exactitude :
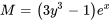

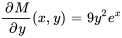
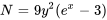

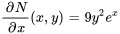
Comme 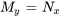 , l’équation est exacte.
, l’équation est exacte.
2) Trouver la solution générale :
Nous avons l’option d’intégrer 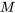 par rapport à
par rapport à  ou d’intégrer
ou d’intégrer 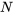 par rapport à
par rapport à  . Comme les deux intégrales sont aussi simples l’une que l’autre, nous intégrons
. Comme les deux intégrales sont aussi simples l’une que l’autre, nous intégrons 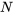 par rapport à
par rapport à  pour varier les choses, en veillant à donner des exemples des deux méthodes.
pour varier les choses, en veillant à donner des exemples des deux méthodes.
1.
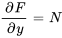
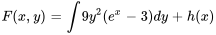
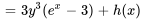
Il importe d’inclure une fonction arbitraire de  ,
, 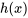 , puisque, cette fois, nous intégrons par rapport à
, puisque, cette fois, nous intégrons par rapport à  .
.
2a. Pour trouver 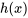 , il faut prendre la dérivée partielle de
, il faut prendre la dérivée partielle de 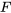 ci-dessus par rapport à
ci-dessus par rapport à  :
:
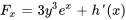
Comme 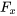 doit être égal à
doit être égal à 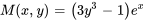 à partir de l’équation différentielle exacte, il faut définir
à partir de l’équation différentielle exacte, il faut définir 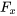 comme étant égal à
comme étant égal à 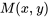 , puis trouver la valeur de
, puis trouver la valeur de 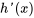 ou la déterminer par comparaison.
ou la déterminer par comparaison.
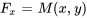
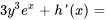

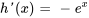
2b. En intégrant 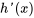 par rapport à
par rapport à  , on obtient
, on obtient . En définissant la constante d’intégration sur zéro, on a
. En définissant la constante d’intégration sur zéro, on a 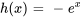 . Par conséquent,
. Par conséquent,
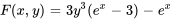
3. Ainsi, l’équation différentielle a pour solution implicite
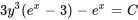
Appliquer la condition initiale :
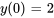
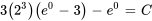
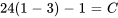
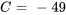
La solution du PVI est donc
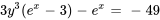
Comme nous devons trouver la solution explicite, nous réarrangeons l’équation afin de trouver la valeur de  :
:
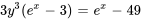
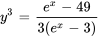
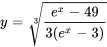
b) Trouver l’intervalle de validité :
Pour établir l’intervalle de validité de la solution, nous devons nous assurer que le dénominateur de la fonction rationnelle n’est pas égal à zéro afin d’éviter les expressions indéfinies :
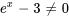
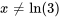
L’intervalle de validité pour la solution est donc
Prenons un exemple
Section 2.3 Exercices
- Détermine si l’équation est exacte et, si tel est le cas, trouve la solution :
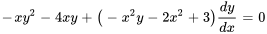 .
.
Afficher/Masquer la réponse
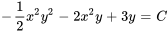
- Résous l’équation différentielle :
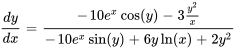 .
.
Afficher/Masquer la réponse
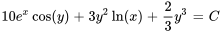
- Résous le problème de valeur initiale. Donne la solution explicite :
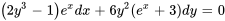 ,
, 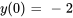 .
.
Afficher/Masquer la réponse