1.2 Champs de direction
S’il est certes utile de disposer d’une formule explicite pour la solution d’une équation différentielle afin de comprendre la nature de la solution, de déterminer où elle augmente ou diminue et d’identifier ses valeurs maximales ou minimales, il est souvent impossible de trouver une telle formule pour la plupart des équations différentielles du monde réel. Par conséquent, d’autres méthodes doivent être employées pour répondre à ces questions. Une approche efficace pour visualiser la solution d’une équation différentielle du premier ordre consiste à créer un champ de direction pour l’équation. Cette méthode donne une représentation graphique du comportement de la solution sans nécessiter de formule explicite.
Supposons que l’équation différentielle du premier ordre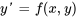 
a des solutions. Pour cette équation, la fonction 
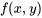donne la pente de la courbe de la solution en n’importe quel du plan XY. Dans un champ de direction, ces pentes sont représentées par de petits segments de droite ou des flèches, tracés en un certain nombre de points du plan. Chaque segment a une pente égale à la valeur de en ce point.
Pour l’équation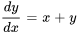 
, le graphique de la solution traversant le point 
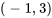doit avoir une pente de
.
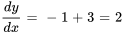La solution générale de l’équation est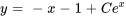 
. Le champ de direction et certaines des solutions de l’équation pour différentes valeurs de la constante 
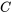sont représentés dans la figure 1.2.1.
Figure 1.2.1 Champs de direction et solutions de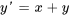 
Les flèches dans les champs de direction représentent les tangentes aux solutions réelles des équations différentielles. Ces flèches peuvent être utilisées comme guides pour dessiner les graphiques des solutions de l’équation différentielle, de façon à obtenir une représentation visuelle du comportement des solutions. En suivant ces flèches, la trajectoire d’une solution peut être visuellement tracée dans le temps, de façon à indiquer son comportement à long terme.