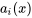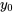1.1 Introduction
A. Définitions
Les équations différentielles (ED) sont des équations mathématiques qui décrivent la relation entre une fonction et ses dérivées, qu’il s’agisse de dérivées ordinaires ou de dérivées partielles. Dans sa forme la plus simple, l’équation différentielle décrit la vitesse à laquelle une quantité change en fonction de la quantité elle-même et de ses dérivées. Les équations différentielles constituent de puissants outils en mathématiques et en sciences, car elles permettent de modéliser un large éventail de phénomènes du monde réel dans diverses disciplines, notamment la physique, l’ingénierie, la biologie, l’économie et bien d’autres. Voici quelques exemples d’équations différentielles.
- Croissance démographique fondamentale :
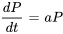
- Décroissance radioactive fondamentale :
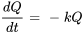
- Lois de refroidissement de Newton :
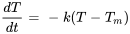
- Deuxième loi du mouvement de Newton :
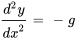
- Circuits RL :
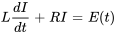
- Circuits RLC :
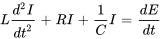
- Équation de la chaleur :
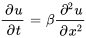
B. Ordre des équations différentielles
L’ordre d’une équation différentielle est l’ordre de la dérivée la plus élevée qui apparaît dans l’équation. Par exemple, si la dérivée la plus élevée est une dérivée seconde, l’équation est du second ordre. Voici quelques exemples :
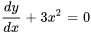 (Premier ordre)
(Premier ordre)
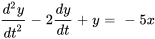 (Second ordre)
(Second ordre)
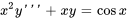 (Troisième ordre)
(Troisième ordre)
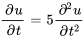 (Second ordre)
(Second ordre)
L’ordre d’une équation différentielle détermine souvent les méthodes employées pour la résoudre. L’ordre d’une équation différentielle est indépendant du type de dérivées impliquées, qu’il s’agisse de dérivées ordinaires ou partielles.
Tout au long de cet ouvrage, nous nous intéresserons principalement aux équations différentielles du premier et du second ordre. Comme vous le découvrirez, les méthodes employées pour résoudre des équations différentielles du second ordre peuvent souvent être facilement étendues aux équations d’ordre supérieur.
Prenons un exemple
C. Équations différentielles ordinaires et partielles
Une équation différentielle ordinaire (EDO) est une équation différentielle impliquant une fonction d’une variable indépendante et ses dérivées. Tous les exemples ci-dessus, à l’exception de l’équation de la chaleur, sont des équations différentielles ordinaires.
Une équation différentielle partielle (EDP) est une équation différentielle qui contient des fonctions inconnues à plusieurs variables et leurs dérivées partielles. Les EDP sont utilisées pour formuler des problèmes impliquant des fonctions de plusieurs variables.
Dans cet ouvrage, nous nous intéresserons avant tout aux équations différentielles ordinaires, qui impliquent des fonctions à variable unique. Nous n’aborderons les équations différentielles partielles que dans le dernier chapitre.
D. Équations différentielles linéaires et non linéaires
Une équation différentielle linéaire est une équation dans laquelle la variable dépendante  et ses dérivées apparaissent à la première puissance, ne sont pas multipliées ensemble et ne sont pas des arguments d’une autre fonction,par exemple
et ses dérivées apparaissent à la première puissance, ne sont pas multipliées ensemble et ne sont pas des arguments d’une autre fonction,par exemple 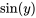 or
or 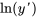 . La forme générale d’une équation différentielle linéaire est la suivante :
. La forme générale d’une équation différentielle linéaire est la suivante :
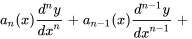
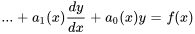
où est la variable dépendante, est la variable indépendante, sont des fonctions de (qui peuvent être constantes ou nulles) et est une fonction de .
Une équation différentielle non linéaire est une équation dans laquelle la variable dépendante ou ses dérivées apparaissent à une puissance supérieure à un, sont multipliées ensemble ou se présentent sous une forme qui n’est pas linéaire. Par exemple, 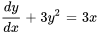 n’est pas linéaire puisque
n’est pas linéaire puisque 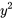 a une puissance de 2.
a une puissance de 2.
Prenons un exemple
E. Équations différentielles homogènes et non homogènes
Une équation différentielle est dite homogène si chacun de ses termes est une fonction de la variable dépendante et de ses dérivées. Concernant les équations différentielles linéaires, une équation est homogène si la fonction 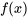 à droite de l’équation est zéro.
à droite de l’équation est zéro.
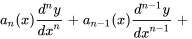
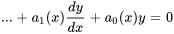
Par exemple, l’équation linéaire 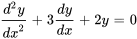 est homogène parce que tous ses termes sont des fonctions de et de ses dérivées et que l’équation est égale à zéro.
est homogène parce que tous ses termes sont des fonctions de et de ses dérivées et que l’équation est égale à zéro.
Une équation différentielle est non homogène si elle comporte des termes qui ne sont pas uniquement des fonctions de la variable dépendante et ses dérivées. Avec les équations linéaires, cela signifie généralement qu’il existe une fonction non nulle du côté de l’équation. Par exemple, l’équation linéaire 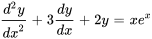 n’est pas homogène à cause de la présence du terme
n’est pas homogène à cause de la présence du terme 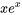 , qui est une fonction de la variable indépendante
, qui est une fonction de la variable indépendante
F. Solutions
Une solution d’équation différentielle est une fonction qui satisfait l’équation sur un intervalle ouvert. Cela signifie que, lorsque la fonction et ses dérivées sont introduites dans l’équation différentielle, l’équation est vraie pour toutes les valeurs de l’intervalle. Il y a souvent un ensemble de solutions.
Vérifiez si 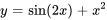 est une solution de
est une solution de 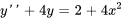 .
.
Afficher/Masquer la solution
Tout d’abord, nous trouvons 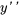 puisque cela apparaît dans l’équation :
puisque cela apparaît dans l’équation :
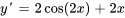

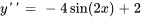 .
.
En remplaçant 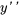 et
et 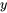 du côté gauche de l’équation, on obtient
du côté gauche de l’équation, on obtient
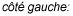
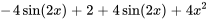
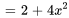
qui est égal au côté droit de l’équation. Puisque 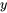 satisfait l’équation, il s’agit d’une solution à l’équation.
satisfait l’équation, il s’agit d’une solution à l’équation.
Prenons un exemple
Prenons maintenant l’équation différentielle 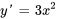 . On peut facilement résoudre cette équation en intégrant :
. On peut facilement résoudre cette équation en intégrant :
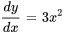
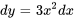
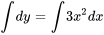
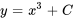
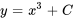 , où
, où 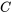 est une constante arbitraire, représentant une famille de solutions à l’équation différentielle donnée. Chaque valeur distincte de
est une constante arbitraire, représentant une famille de solutions à l’équation différentielle donnée. Chaque valeur distincte de 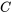 donne une solution particulière unique, montrant comment diverses conditions initiales peuvent être satisfaites. Cette famille de solutions, qui recoupe toutes les solutions possibles grâce à l’inclusion de la constante arbitraire
donne une solution particulière unique, montrant comment diverses conditions initiales peuvent être satisfaites. Cette famille de solutions, qui recoupe toutes les solutions possibles grâce à l’inclusion de la constante arbitraire 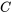 , est ce que l’on appelle la solution générale de l’équation différentielle.
, est ce que l’on appelle la solution générale de l’équation différentielle.
Une solution explicite exprime explicitement la variable dépendante en fonction de la ou des variable(s) indépendante(s). Par exemple, 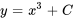 est une solution explicite. Par ailleurs, une solution implicite peut ne pas exprimer directement la variable dépendante, mais satisfait néanmoins l’équation différentielle. Par exemple,
est une solution explicite. Par ailleurs, une solution implicite peut ne pas exprimer directement la variable dépendante, mais satisfait néanmoins l’équation différentielle. Par exemple, 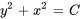 . Il faut savoir qu’il n’est pas toujours possible de trouver une solution explicite.
. Il faut savoir qu’il n’est pas toujours possible de trouver une solution explicite.
G. Conditions initiales
Les conditions initiales renvoient aux valeurs spécifiées pour la variable dépendante et éventuellement ses dérivées en un point spécifique. Les conditions initiales permettent de déterminer la solution spécifique (ou particulière) d’une équation différentielle à partir de la solution générale, qui comporte normalement des constantes arbitraires. Par exemple, 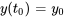 dit que, à l’instant
dit que, à l’instant 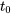 , la valeur de est . Le nombre de conditions initiales requises pour une équation différentielle donnée dépend de l’ordre de l’équation différentielle. En général, une équation différentielle d’ordre
, la valeur de est . Le nombre de conditions initiales requises pour une équation différentielle donnée dépend de l’ordre de l’équation différentielle. En général, une équation différentielle d’ordre 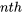 nécessite des
nécessite des 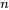 conditions initiales. Ces conditions spécifient les valeurs de la fonction et de ses dérivées jusqu’au
conditions initiales. Ces conditions spécifient les valeurs de la fonction et de ses dérivées jusqu’au 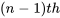 ordre en un point particulier. Par exemple, une équation différentielle de second ordre nécessite deux conditions initiales. Il s’agit souvent de la valeur de la fonction et de la valeur de la première dérivée en un point spécifié.
ordre en un point particulier. Par exemple, une équation différentielle de second ordre nécessite deux conditions initiales. Il s’agit souvent de la valeur de la fonction et de la valeur de la première dérivée en un point spécifié.
Un problème de valeur initiale (PVI) est une équation différentielle avec une ou plusieurs condition(s) initiale(s) qui donne(nt) une solution particulière. Une solution peut ne pas être valable pour tous les nombres réels – il existe un « intervalle de validité », le domaine de la solution.
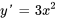 ,
, 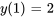 est un problème de valeur initiale, où
est un problème de valeur initiale, où 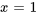 et
et 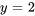 peuvent être substitués dans la solution générale de
peuvent être substitués dans la solution générale de 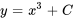 pour trouver
pour trouver 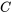 , ce qui donne une solution particulière de
, ce qui donne une solution particulière de 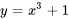 .
.

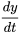 ,
,