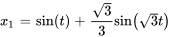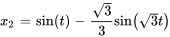6.10 Applications
A. Introduction
Dans cette section, nous revenons sur l’application des équations différentielles dans la modélisation des systèmes d’ingénierie. En particulier, nous nous intéressons aux vibrations mécaniques et aux circuits électriques, deux grands domaines donnant lieu à l’application de systèmes d’équations différentielles.
Les équations différentielles sont d’une grande utilité dans divers domaines d’ingénierie. En génie chimique, elles sont essentielles pour modéliser la cinétique des réactions et la dynamique des processus, notamment dans des scénarios tels que les problèmes de mélanges impliquant plusieurs réservoirs et substances, des facteurs déterminants pour la conception des réacteurs et l’optimisation des processus. En génie civil, les modèles d’équations différentielles sont indispensables pour évaluer la sécurité et la longévité des structures soumises à diverses conditions de charge, comme dans l’analyse de la résistance sismique des bâtiments à plusieurs étages. L’ingénierie aérospatiale se sert de ces équations pour simuler le mouvement des avions et des engins spatiaux, en y intégrant à la fois la dynamique de translation et la dynamique de rotation. Ces connaissances sont primordiales pour élaborer des systèmes de contrôle qui améliorent la stabilité et la manœuvrabilité. L’ingénierie environnementale utilise également des modèles d’équations différentielles pour suivre la propagation des polluants, ce qui permet de concevoir des mesures efficaces de protection de l’environnement.
B. Circuits électriques
Les lois de Kirchhoff, que nous avons vues à la section 2.5, servent de base à la dérivation des équations directrices. Ces lois facilitent l’analyse des circuits en fournissant une approche systématique du calcul des courants et des tensions en divers points du circuit. Dans les circuits plus complexes, par exemple les circuits série-parallèle,
a) Pour le schéma de circuit électrique donné, déterminer le système d’équations différentielles qui décrit les courants dans les différentes branches du circuit. On suppose que tous les courants initiaux sont nuls. b) Une fois que le système d’équations différentielles et les conditions initiales sont établis, résoudre le système pour les courants dans chaque branche du circuit.
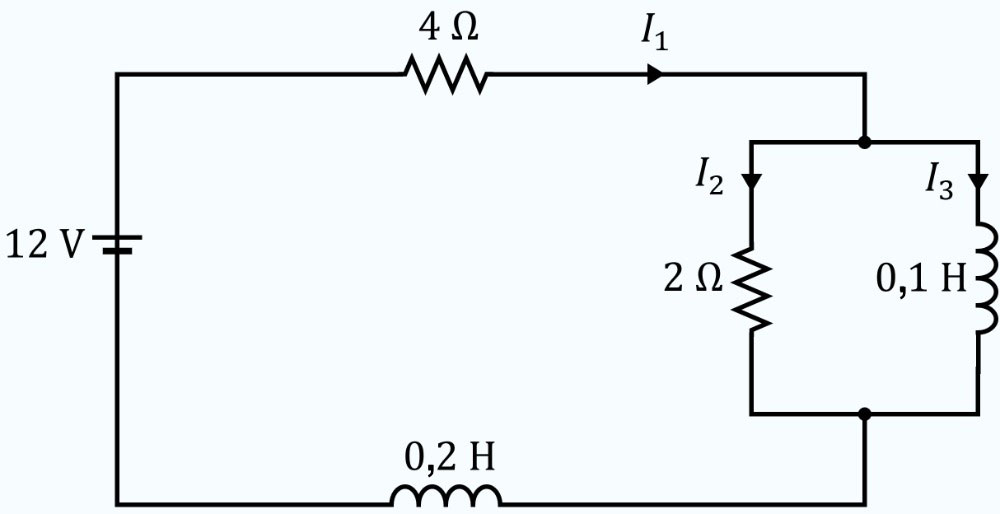
Description du schéma
Afficher/Masquer la solution
a) Dans l’exemple 4.8.2, nous avons examiné ce circuit RL et l’avons analysé avec la transformée de Laplace. Dans cet exemple, nous résolvons le même circuit avec la méthode matricielle. Les équations du système pour le circuit sont les suivantes, avec pour conditions initiales la nullité de tous les courants à l’instant 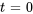 .
.
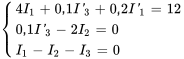

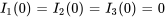 (6.10.1)
(6.10.1)
b) Étapes de résolution du système :
1. Le système de la section 6.10.1 est un mélange d’équations différentielles et d’équations algébriques. Il faut d’abord convertir ce système en un système d’équations différentielles linéaires en utilisant la deuxième équation pour exprimer 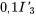 en tant que
en tant que  dans la première équation et en isolant les premières dérivées dans les deux premières équations. Ce qui donne :
dans la première équation et en isolant les premières dérivées dans les deux premières équations. Ce qui donne :
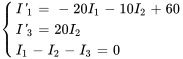

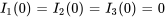 (6.10.1)
(6.10.1)
Pour créer un système d’équations différentielles linéaires à partir du système donné, il faut tenir compte du fait que 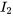 n’a pas de dérivée présente. Pour contourner ce problème, il faut éliminer
n’a pas de dérivée présente. Pour contourner ce problème, il faut éliminer 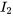 des équations. Pour ce faire, on réarrange la troisième équation de façon à exprimer
des équations. Pour ce faire, on réarrange la troisième équation de façon à exprimer 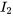 en termes de
en termes de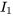 et
et 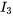 , puis on remplace cette expression par
, puis on remplace cette expression par 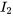 dans les autres équations.
dans les autres équations.
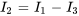 (6.10.2)
(6.10.2)
On simplifie ensuite le système en
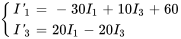

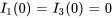 (6.10.2)
(6.10.2)
2. On exprime ensuite le problème de valeur initiale (PVI) sous forme matricielle.
![bb(I)'=[(-30,10),(20,-20)] bb(I)+[(60),(0)], bb(I)'=[(-30,10),(20,-20)] bb(I)+[(60),(0)],](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/17de568f58e36fe6148b568656fcb261.png)
![bb(I)(0)=[(0),(0)] bb(I)(0)=[(0),(0)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/59e432c048d6932b439764b0dec96f8c.png)
3. Ensuite, on trouve une solution fondamentale au système complémentaire associé (homogène). Le polynôme caractéristique de  est donné par
est donné par
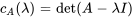
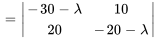
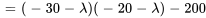
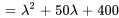
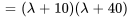
Les valeurs propres et les vecteurs propres correspondants sont
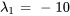 :
: ![bb(u)_1=[(1),(2)] bb(u)_1=[(1),(2)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/1c1d03aad5acdc2859530199692c81be.png)
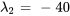 :
: ![bb(u)_1=[(-1),(1)] bb(u)_1=[(-1),(1)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/df09fdb5df817afd8006545d216b2cce.png)
Par conséquent, ![{e^(-10t) [(1),(2)], \ e^(-40t) [(-1),(1)] } {e^(-10t) [(1),(2)], \ e^(-40t) [(-1),(1)] }](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/064b7aa8876b583ac3942c72b5e26e3f.png) est un ensemble fondamental de solutions au système complémentaire.
est un ensemble fondamental de solutions au système complémentaire.
Ainsi, la matrice fondamentale 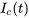 pour le système complémentaire est
pour le système complémentaire est
![I_c(t)=[(e^(-10t),-e^(-40t)),(2e^(-10t),e^(-40t))] I_c(t)=[(e^(-10t),-e^(-40t)),(2e^(-10t),e^(-40t))]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/0427d8ed908c32cca6bd9dfa5363862a.png)
3. Il faut maintenant déterminer une solution particulière du système.
(i) Déterminer 
![I_c^-1(t)=1/3[(e^(10t),e^(10t)),(-2e^(40t),e^(40t))] I_c^-1(t)=1/3[(e^(10t),e^(10t)),(-2e^(40t),e^(40t))]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/78e7a6299914cf8605798c2493fd60f7.png)
(ii) Déterminer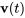 en définissant une constante d’intégration nulle
en définissant une constante d’intégration nulle
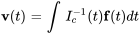
![=int \ [(e^(10t),e^(10t)),(-2e^(40t),e^(40t))] [(60),(0)] dt =int \ [(e^(10t),e^(10t)),(-2e^(40t),e^(40t))] [(60),(0)] dt](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/2ba0b8522b557eea386d23f50cd002f1.png)
![=[(2e^(10t)),(-e^(40t))] =[(2e^(10t)),(-e^(40t))]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/5b9da92cf9760cc7e9a48e3e28d22a0a.png)
Une solution particulière du système est donc donnée par
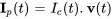
![=[(e^(-10t),-e^(-40t)),(2e^(-10t),e^(-40t))] [(2e^(10t)),(-e^(40t))] =[(e^(-10t),-e^(-40t)),(2e^(-10t),e^(-40t))] [(2e^(10t)),(-e^(40t))]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/e513cdec178b8f80b0fbaa04017c482c.png)
![=[(3),(3)] =[(3),(3)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/7cfe4ad1afdfb45ab51d5dd5af07b84f.png)
4. Une solution générale du système est donc donnée par
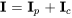
![=[(3),(3)] =[(3),(3)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/7cfe4ad1afdfb45ab51d5dd5af07b84f.png)
![+c_1e^(-10t) [(1),(2)] +c_2e^(-40t) [(-1),(1)] +c_1e^(-10t) [(1),(2)] +c_2e^(-40t) [(-1),(1)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/1d8ed9fff79a2c456ab0414d35a7fca0.png)
5. On applique maintenant les conditions initiales pour trouver les constantes dans la solution générale.
![bb(I)(0)=[(0),(0)] bb(I)(0)=[(0),(0)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/59e432c048d6932b439764b0dec96f8c.png)
![[(3),(3)] [(3),(3)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/cd64ae3c2ba7f96a0f0e665e718f11df.png)
![+c_1e^(-10t) [(1),(2)] +c_2e^(-40t) [(-1),(1)]=[(0),(0)] +c_1e^(-10t) [(1),(2)] +c_2e^(-40t) [(-1),(1)]=[(0),(0)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/4c7c7d21f7162b4042f4181629836b02.png)
On obtient ainsi un système de deux équations à deux inconnues.
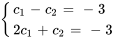
En résolvant le système, on obtient

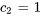
La solution du problème de valeur initiale est donc
![bb(I)=[(3),(3)] bb(I)=[(3),(3)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/b569551c19338ff3b650f7e7774b2738.png)
![-2e^(-10t) [(1),(2)] +e^(-40t) [(-1),(1)] -2e^(-10t) [(1),(2)] +e^(-40t) [(-1),(1)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/f3a912dda20a2d0ffb6becb48aa58ef8.png)
Cela donne, dans les expressions finales pour 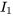 et
et 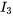 :
:
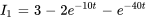
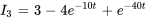
6. Pour trouver 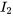 , on remplace à nouveau l’expression par
, on remplace à nouveau l’expression par 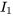 et
et 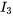 dans l’équation (6.10.1), ce qui donne
dans l’équation (6.10.1), ce qui donne
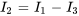
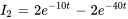
C. Vibrations mécaniques
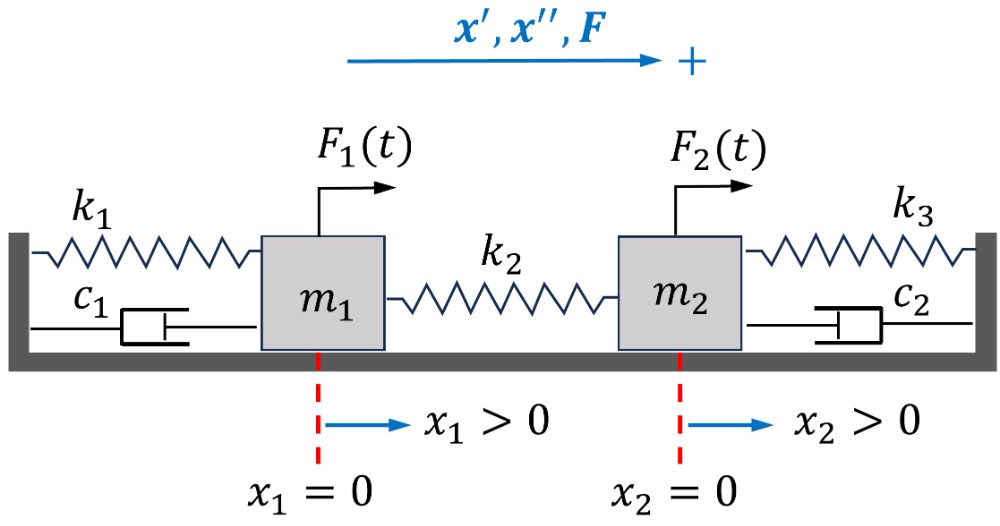
L’analyse des vibrations mécaniques est cruciale pour concevoir des systèmes résistants aux charges dynamiques. Un modèle plus réaliste qui capture l’essence des systèmes mécaniques implique de considérer non seulement les masses et les ressorts, mais aussi les éléments d’amortissement et les forces externes. Cette section se concentre sur un système composé de deux masses reliées par des ressorts dans un arrangement horizontal, avec amortissement et des forces externes agissant sur les deux masses. Un tel modèle peut représenter un large éventail d’applications techniques, des suspensions de véhicules aux composants de machines. Un schéma du système est présenté à la figure 6.10.1.
Hypothèses
Pour procéder à la dérivation des équations du mouvement du système, on fait les hypothèses suivantes :
- Amortissement linéaire : chaque masse est couplée à un élément d’amortissement, caractérisé par les coefficients d’amortissement linéaire
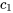 pour
pour  et
et 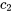 pour
pour 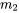 . Ces coefficients quantifient la résistance au mouvement de chaque masse.
. Ces coefficients quantifient la résistance au mouvement de chaque masse. - Forces externes : des forces externes dépendantes du temps
 et
et 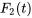 agissent respectivement sur
agissent respectivement sur  et
et 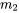 et sont considérées comme positives dans la direction droite.
et sont considérées comme positives dans la direction droite. - Élasticité linéaire : les ressorts obéissent à la loi de Hooke, c’est-à-dire que la force exercée sur chaque ressort est directement proportionnelle à son déplacement par rapport à la longueur de repos.
- Petits déplacements : l’analyse suppose de petits déplacements à partir du point d’équilibre, ce qui autorise la linéarisation du système. Les déplacements sont réputés être positifs lorsqu’ils sont orientés vers la droite.
- Corps rigide : les masses sont traitées comme des points matériels, tandis que les ressorts et les amortissements sont censés être de masse nulle, se concentrant uniquement sur les forces et déplacements axiaux.
Configuration du système
Nous considérons un cas général avec un système constitué de deux masses,  et
et 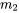 , reliées par trois ressorts aux constantes de rigidité
, reliées par trois ressorts aux constantes de rigidité 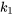 ,
, 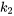 et
et 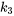 et augmentées par deux amortisseurs. Les ressorts extérieurs sont attachés à des parois fixes. Les forces externes agissent sur les masses et les amortisseurs contrecarrent leurs mouvements. Cette structure permet d’ajuster les forces externes et les effets d’amortissement, de façon à s’adapter aux scénarios dans lesquels ces forces sont absentes en fixant leurs valeurs respectives à zéro.
et augmentées par deux amortisseurs. Les ressorts extérieurs sont attachés à des parois fixes. Les forces externes agissent sur les masses et les amortisseurs contrecarrent leurs mouvements. Cette structure permet d’ajuster les forces externes et les effets d’amortissement, de façon à s’adapter aux scénarios dans lesquels ces forces sont absentes en fixant leurs valeurs respectives à zéro.
Dériver le système d’équations différentielles pour le système couplé amorti et forcé décrit ci-dessus (figure 6.10.1).
Afficher/Masquer la solution
La dynamique de ce système amorti avec des forces externes est régie par deux équations différentielles linéaires couplées du second ordre, reflétant l’équilibre des forces sur chaque masse. Ici, on considère que la direction des forces externes est vers la droite et que les déplacements sont également positifs (sur la droite), en supposant que le déplacement de la masse 1, 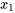 , est supérieur au déplacement de la masse 2,
, est supérieur au déplacement de la masse 2, 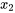 , de sorte que
, de sorte que  /span>.
/span>.
1) Les forces agissant sur la masse  sont
sont
- Force de rappel du ressort
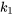 ,
,  .
. - Force de rappel du ressort
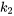 ,
, 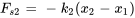 , où
, où  est le déplacement du ressort du milieu.
est le déplacement du ressort du milieu. - Force d’amortissement
 , où
, où 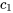 est le coefficient d’amortissement de l’amortisseur 1. Si elle est présente, la force d’amortissement est proportionnelle à la vitesse de la masse, mais dans la direction opposée au mouvement.
est le coefficient d’amortissement de l’amortisseur 1. Si elle est présente, la force d’amortissement est proportionnelle à la vitesse de la masse, mais dans la direction opposée au mouvement. - Force externe
 . Il s’agit de toute force externe agissant sur la masse
. Il s’agit de toute force externe agissant sur la masse  , qui peut être périodique ou aléatoire, et induisant des vibrations forcées.
, qui peut être périodique ou aléatoire, et induisant des vibrations forcées.

D’après la deuxième loi du mouvement de Newton,
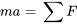
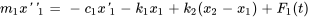
Cette équation peut être simplifiée en
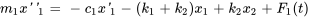
On remarque que, comme 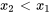 , le ressort
, le ressort 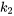 est comprimé et la force qu’il exerce sur la masse 1 est orientée vers la gauche (négative), le but étant de rétablir le ressort à sa longueur d’équilibre.
est comprimé et la force qu’il exerce sur la masse 1 est orientée vers la gauche (négative), le but étant de rétablir le ressort à sa longueur d’équilibre.
2) Les forces agissant sur la masse 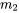 sont
sont
- Force de rappel du ressort
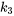 ,
,  .
. - Force de rappel du ressort
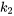 ,
, 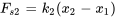 , où
, où  est le déplacement du ressort du milieu.
est le déplacement du ressort du milieu. - Force d’amortissement
 , où
, où 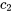 est le coefficient d’amortissement de l’amortisseur 2. Si elle est présente, la force d’amortissement est proportionnelle à la vitesse de la masse, mais dans la direction opposée au mouvement.
est le coefficient d’amortissement de l’amortisseur 2. Si elle est présente, la force d’amortissement est proportionnelle à la vitesse de la masse, mais dans la direction opposée au mouvement. - Force externe
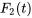 . Il s’agit de toute force externe agissant sur la masse
. Il s’agit de toute force externe agissant sur la masse 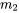 , qui peut être périodique ou aléatoire, et induisant des vibrations forcées.
, qui peut être périodique ou aléatoire, et induisant des vibrations forcées.
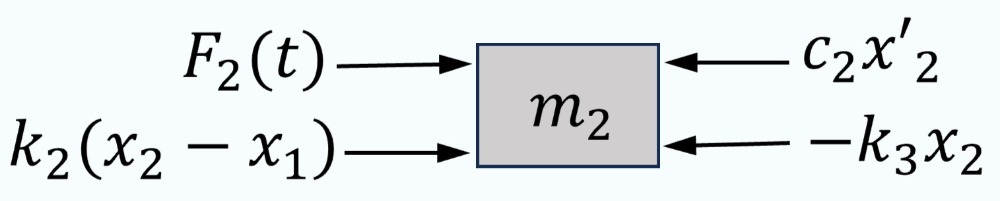
D’après la deuxième loi du mouvement de Newton,
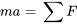
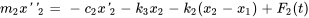
Cette équation peut être simplifiée en
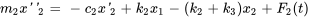
On remarque que, comme 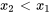 , le ressort
, le ressort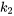 est comprimé et la force qu’il exerce sur la masse 2 est orientée vers la droite et devrait être positive, ce qui est cohérent avec le signe de
est comprimé et la force qu’il exerce sur la masse 2 est orientée vers la droite et devrait être positive, ce qui est cohérent avec le signe de .
.
Par conséquent, les déplacements dépendants du temps des masses sont décrits par le système d’équations différentielles
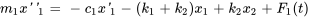
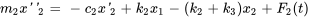
a) Réécrire le système dérivé d’équations différentielles de l’exemple 6.10.2 en un système d’équations du premier ordre. b) Écrire le système sous forme matricielle.
Afficher/Masquer la solution
a) Les équations régissant la système masse-ressort de la figure 6.10.1 sont dérivées dans l’exemple 6.10.2.
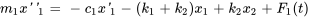
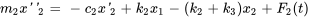
La section 6.4-C a expliqué comment convertir des équations différentielles d’ordre supérieur en un système d’équations du premier ordre. On introduit de nouvelles variables comme suit :
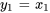 ,
, 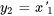 ,
, 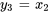 , et
, et 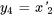
Les équations peuvent alors être écrites comme suit :
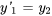
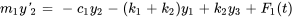
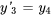

b) Le système sous forme matricielle est

![bb(y)'(t)=[(0,1,0,0),(-(k_1+k_2)/(m_1),(c_1)/(m_1),(k_2)/(m_1),0),(0,0,0,1),((k_2)/(m_2),0,-(k_2+k_3)/(m_2) ,-(c_2)/(m_2))] bb(y)'(t)=[(0,1,0,0),(-(k_1+k_2)/(m_1),(c_1)/(m_1),(k_2)/(m_1),0),(0,0,0,1),((k_2)/(m_2),0,-(k_2+k_3)/(m_2) ,-(c_2)/(m_2))]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/ce310c7d5b4cce79f6e3b2f11d0b6e39.png)
![bb(y)(t)+[(0),((F_1(t))/(m_1)),(0),((F_2(t))/(m_2)) ] bb(y)(t)+[(0),((F_1(t))/(m_1)),(0),((F_2(t))/(m_2)) ]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/f867fcf9fe06c04755c538d99bc7ab61.png)
Considérons un système masse-ressort couplé, tel celui de l’exemple 6.10.2, avec les paramètres suivants : les deux masses  et
et 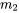 pèsent 1 kg et toutes les constantes du ressort
pèsent 1 kg et toutes les constantes du ressort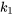 ,
, 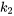 et
et 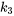 sont de 1 N/m. Le système est isolé contre les forces externes et les effets d’amortissement. Au départ, les déplacements et les vitesses sont
sont de 1 N/m. Le système est isolé contre les forces externes et les effets d’amortissement. Au départ, les déplacements et les vitesses sont 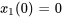 m,
m,  m/s,
m/s, 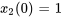 m et
m et 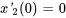 m/s. Résoudre le problème de valeur initiale pour déterminer les déplacements des masses en fonction du temps. Étant donné la complexité des calculs, utiliser un logiciel d’algèbre matricielle pour trouver les valeurs propres et les vecteurs propres.
m/s. Résoudre le problème de valeur initiale pour déterminer les déplacements des masses en fonction du temps. Étant donné la complexité des calculs, utiliser un logiciel d’algèbre matricielle pour trouver les valeurs propres et les vecteurs propres.
Afficher/Masquer la solution
Informations données :
-
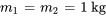
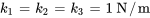
- Pas d’amortissement :
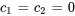
- Pas de forces externes :
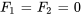
- Conditions initiales :
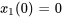 ,
, 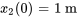 ,
, 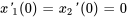
Dans l’exemple 6.10.3, on a converti un système du second ordre régissant le système masse-ressort couplé en un système du premier ordre et on l’a exprimé en notation matricielle.

![bb(y)'(t)=[(0,1,0,0),(-(k_1+k_2)/(m_1),(c_1)/(m_1),(k_2)/(m_1),0),(0,0,0,1),((k_2)/(m_2),0,-(k_2+k_3)/(m_2) ,-(c_2)/(m_2))] bb(y)'(t)=[(0,1,0,0),(-(k_1+k_2)/(m_1),(c_1)/(m_1),(k_2)/(m_1),0),(0,0,0,1),((k_2)/(m_2),0,-(k_2+k_3)/(m_2) ,-(c_2)/(m_2))]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/ce310c7d5b4cce79f6e3b2f11d0b6e39.png)
![bb(y)(t)+[(0),((F_1(t))/(m_1)),(0),((F_2(t))/(m_2)) ] bb(y)(t)+[(0),((F_1(t))/(m_1)),(0),((F_2(t))/(m_2)) ]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/f867fcf9fe06c04755c538d99bc7ab61.png)
où
![bb(y)=[(y_1),(y_2),(y_3),(y_4)]=[(x_1),(x'_1),(x_2),(x'_2)] bb(y)=[(y_1),(y_2),(y_3),(y_4)]=[(x_1),(x'_1),(x_2),(x'_2)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/6ead37e9844db7674e33f1e5e5c72d9e.png)
En remplaçant les valeurs données, le problème de valeur initial devient
![bb(y)'(t)=[(0,1,0,0),(-2,0,1,0),(0,0,0,1),(1,0,-2 ,0)] bb(y)'(t)=[(0,1,0,0),(-2,0,1,0),(0,0,0,1),(1,0,-2 ,0)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/a7db0bf2da8f5dd02a945f478efe1da7.png)
![bb(y)(t), \ \ bb(y)(0)=[(0),(0),(1),(0) ] bb(y)(t), \ \ bb(y)(0)=[(0),(0),(1),(0) ]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/698d1c885cd3cf844b1a6784ecdcad3b.png)
En utilisant un logiciel d’algèbre matricielle, on trouve les valeurs propres et les vecteurs propres de la matrice coefficient. Les valeurs propres et les vecteurs propres se présentent sous la forme des paires complexes conjuguées suivantes :
Vecteur propre pour 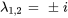 :
: ![bb(u)_(1,2)=[(0),(1),(0),(1)]+-i [(-1),(0),(-1),(0)] bb(u)_(1,2)=[(0),(1),(0),(1)]+-i [(-1),(0),(-1),(0)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/7dcf02a0ab3cb91ba3bfb72a726ffa4a.png)
Vecteur propre pour 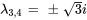 :
: ![bb(u)_(3,4)=[(0),(-3),(0),(3)]+-i [(sqrt(3)),(0),(-sqrt(3)),(0)] bb(u)_(3,4)=[(0),(-3),(0),(3)]+-i [(sqrt(3)),(0),(-sqrt(3)),(0)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/63e1d7e529fb616585680175d65aaf89.png)
La solution pour chaque paire est donnée par l’équation présentée à la section 6.7.1.
Pour la première paire, 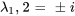 , les deux solutions linéairement indépendantes sont
, les deux solutions linéairement indépendantes sont
![bb"y"_1=[(0),(1),(0),(1)] cos(t)-[(-1),(0),(-1),(0)] sin( t)= bb"y"_1=[(0),(1),(0),(1)] cos(t)-[(-1),(0),(-1),(0)] sin( t)=](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/5617cb55270d2dbe12a325818021ba33.png)
![[(sin(t)),(cos(t)),(sin(t)),(cos(t))] [(sin(t)),(cos(t)),(sin(t)),(cos(t))]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/8c3b481db38762e1ce5e9666b100bcbf.png)
![bb"y"_2=[(0),(1),(0),(1)] sin(t)+[(-1),(0),(-1),(0)]cos( t)= bb"y"_2=[(0),(1),(0),(1)] sin(t)+[(-1),(0),(-1),(0)]cos( t)=](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/f2ba801bbe97fe2bf41308d23153f7de.png)
![[(-cos(t)),(sin(t)),(-cos(t)),(sin(t))] [(-cos(t)),(sin(t)),(-cos(t)),(sin(t))]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/7ade188ab69d14406fec6ca72e9b69ee.png)
Pour la seconde paire, 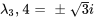 , les deux solutions linéairement indépendantes sont
, les deux solutions linéairement indépendantes sont
![bb"y"_3=[(0),(-3),(0),(3)] cos(sqrt(3) t)-[(sqrt(3)),(0),(-sqrt(3)),(0)] sin( sqrt(3) t)= bb"y"_3=[(0),(-3),(0),(3)] cos(sqrt(3) t)-[(sqrt(3)),(0),(-sqrt(3)),(0)] sin( sqrt(3) t)=](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/973eea282e06eb051aa43c5774aad673.png)
![[(-sqrt(3) sin(sqrt(3) t)),(-3cos(sqrt(3) t)),(sqrt(3) sin(sqrt(3) t)),(3cos(sqrt(3) t))] [(-sqrt(3) sin(sqrt(3) t)),(-3cos(sqrt(3) t)),(sqrt(3) sin(sqrt(3) t)),(3cos(sqrt(3) t))]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/679114a2d2dca086e4b7970db2e6e049.png)
![bb"y"_4=[(0),(-3),(0),(3)] sin(sqrt(3) t)+[(sqrt(3)),(0),(-sqrt(3)),(0)] cos( sqrt(3) t)= bb"y"_4=[(0),(-3),(0),(3)] sin(sqrt(3) t)+[(sqrt(3)),(0),(-sqrt(3)),(0)] cos( sqrt(3) t)=](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/b4a365690dd809c4d25c87a9451931e0.png)
![[(sqrt(3) cos(sqrt(3) t)),(-3sin(sqrt(3) t)),(-sqrt(3) cos(sqrt(3) t)),(3sin(sqrt(3) t))] [(sqrt(3) cos(sqrt(3) t)),(-3sin(sqrt(3) t)),(-sqrt(3) cos(sqrt(3) t)),(3sin(sqrt(3) t))]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/e3b0651b9bc9694fcfafc66e69ea3927.png)
La matrice fondamentale du système est donc
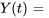
![[(bb(y)_1,bb(y)_2, bb(y)_3, bb(y)_4)] [(bb(y)_1,bb(y)_2, bb(y)_3, bb(y)_4)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/77e5c54fbb95f0b5f43f7333322df5bd.png)
![= [(sin(t),-cos(t),-sqrt(3) sin(sqrt(3) t),sqrt(3) cos(sqrt(3) t)),(cos(t),sin(t),-3 cos(sqrt(3) t),-3sin(sqrt(3) t)),(sin(t),-cos(t),sqrt(3) sin(sqrt(3) t),-sqrt(3) cos(sqrt(3) t)),(cos(t),sin(t),3 cos(sqrt(3) t),3 sin(sqrt(3) t))] = [(sin(t),-cos(t),-sqrt(3) sin(sqrt(3) t),sqrt(3) cos(sqrt(3) t)),(cos(t),sin(t),-3 cos(sqrt(3) t),-3sin(sqrt(3) t)),(sin(t),-cos(t),sqrt(3) sin(sqrt(3) t),-sqrt(3) cos(sqrt(3) t)),(cos(t),sin(t),3 cos(sqrt(3) t),3 sin(sqrt(3) t))]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/601fa47b2cd520c7982e4dbbc12680b6.png)
La solution générale du système sous forme matricielle est
![bb(y)(t)= [(sin(t),-cos(t),-sqrt(3) sin(sqrt(3) t),sqrt(3) cos(sqrt(3) t)),(cos(t),sin(t),-3 cos(sqrt(3) t),-3sin(sqrt(3) t)),(sin(t),-cos(t),sqrt(3) sin(sqrt(3) t),-sqrt(3) cos(sqrt(3) t)),(cos(t),sin(t),3 cos(sqrt(3) t),3 sin(sqrt(3) t))] bb(y)(t)= [(sin(t),-cos(t),-sqrt(3) sin(sqrt(3) t),sqrt(3) cos(sqrt(3) t)),(cos(t),sin(t),-3 cos(sqrt(3) t),-3sin(sqrt(3) t)),(sin(t),-cos(t),sqrt(3) sin(sqrt(3) t),-sqrt(3) cos(sqrt(3) t)),(cos(t),sin(t),3 cos(sqrt(3) t),3 sin(sqrt(3) t))]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/ede967ace86f9e5be043e13235c01ab5.png)
![[(c_1),(c_2),(c_3),(c_4)] [(c_1),(c_2),(c_3),(c_4)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/c45f9355d1ce74d1e106597eb503cca6.png)
En appliquant les conditions initiales, on obtient
![bb(y)(0)=[(0),(0),(1),(0) ] bb(y)(0)=[(0),(0),(1),(0) ]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/e09334cb97cec1b194b0661782673030.png)
![[(0,-1,0,sqrt(3)),(1,0,-3,0),(0,-1,0,-sqrt(3)),(1,0,3 ,0)] [(0,-1,0,sqrt(3)),(1,0,-3,0),(0,-1,0,-sqrt(3)),(1,0,3 ,0)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/f7c228b13a28affbcd4a1e6950dcbecd.png)
![[(c_1),(c_2),(c_3),(c_4)] [(c_1),(c_2),(c_3),(c_4)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/c45f9355d1ce74d1e106597eb503cca6.png)
![=[(0),(0),(1),(0) ] =[(0),(0),(1),(0) ]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/dfbd4d77a475401e4be11534640c72a1.png)
En résolvant les coefficients, on trouve
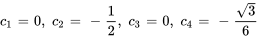
La solution du problème de valeur initiale est donc
![bb(y)(t)= [(sin(t),-cos(t),-sqrt(3) sin(sqrt(3) t),sqrt(3) cos(sqrt(3) t)),(cos(t),sin(t),-3 cos(sqrt(3) t),-3sin(sqrt(3) t)),(sin(t),-cos(t),sqrt(3) sin(sqrt(3) t),-sqrt(3) cos(sqrt(3) t)),(cos(t),sin(t),3 cos(sqrt(3) t),3 sin(sqrt(3) t))] bb(y)(t)= [(sin(t),-cos(t),-sqrt(3) sin(sqrt(3) t),sqrt(3) cos(sqrt(3) t)),(cos(t),sin(t),-3 cos(sqrt(3) t),-3sin(sqrt(3) t)),(sin(t),-cos(t),sqrt(3) sin(sqrt(3) t),-sqrt(3) cos(sqrt(3) t)),(cos(t),sin(t),3 cos(sqrt(3) t),3 sin(sqrt(3) t))]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/ede967ace86f9e5be043e13235c01ab5.png)
![[(0),(-1/2),(0),(-sqrt(3)/6)] [(0),(-1/2),(0),(-sqrt(3)/6)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/a7328b65996b96bdf11655e6cf4ceccf.png)
Elle peut s’écrire comme suit
![bb(y)=[(y_1),(y_2),(y_3),(y_4)] bb(y)=[(y_1),(y_2),(y_3),(y_4)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/a698eccc789d16c0387900eb67ebac57.png)

![[(1/2cos(t)-1/2cos(sqrt(3)t)),(-1/2sin(t)+(sqrt(3))/2sin(sqrt(3)t)),(1/2cos(t)+1/2cos(sqrt(3)t)),(-1/2sin(t)-(sqrt(3))/2sin(sqrt(3)t))] [(1/2cos(t)-1/2cos(sqrt(3)t)),(-1/2sin(t)+(sqrt(3))/2sin(sqrt(3)t)),(1/2cos(t)+1/2cos(sqrt(3)t)),(-1/2sin(t)-(sqrt(3))/2sin(sqrt(3)t))]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/542c1c51d5c60ffaf23184052651a975.png)
Rappelons que, dans l’exemple 10.6.3, on a introduit des variables  pour représenter les déplacements et les vitesses des masses.
pour représenter les déplacements et les vitesses des masses.
![[(y_1),(y_2),(y_3),(y_4)]=[(x_1),(x'_1),(x_2),(x'_2)] [(y_1),(y_2),(y_3),(y_4)]=[(x_1),(x'_1),(x_2),(x'_2)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/4717b1fc82ce444670b544be6bbfe49d.png)
Étant donné cette conversion, les déplacements de la masse 1 (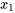 ) et de la masse 2 (
) et de la masse 2 (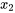 ) en fonction du temps sont déterminés par
) en fonction du temps sont déterminés par
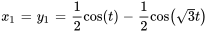
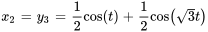
La représentation graphique ci-dessous montre les déplacements des deux masses au fil du temps dans un système masse-ressort couplé dans cet exemple, sur un graphique avec le temps sur l’axe horizontal (allant de 0 à 10 secondes) et le déplacement en mètres sur l’axe vertical. La ligne pour la masse 1 oscille, soit un modèle de mouvement qui varie entre des déplacements positifs et des déplacements négatifs, suggérant un mouvement harmonique complexe. La ligne de la masse 2 suit un schéma oscillatoire similaire, mais avec des différences de phase et d’amplitude par rapport à la masse 1, reflétant l’interaction entre les deux masses au moyen du système de ressorts.
Section 6.10 Exercices
- Considère un système masse-ressort couplé, tel celui de l’exemple 6.10.2, avec les paramètres suivants : les masses
 et
et 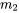 pèsent 1 kg et toutes les constantes du ressort
pèsent 1 kg et toutes les constantes du ressort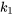 ,
, 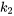 et
et 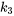 sont de 1 N/m. Le système est isolé contre les forces externes et les effets d’amortissement. Au départ, les déplacements et les vitesses sont
sont de 1 N/m. Le système est isolé contre les forces externes et les effets d’amortissement. Au départ, les déplacements et les vitesses sont 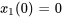 m,
m,  m/s,
m/s,  m et
m et 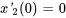 m/s. Résoudre le problème de valeur initiale pour déterminer les déplacements des masses en fonction du temps. Utilise un logiciel d’algèbre matricielle pour trouver les valeurs propres et les vecteurs propres.
m/s. Résoudre le problème de valeur initiale pour déterminer les déplacements des masses en fonction du temps. Utilise un logiciel d’algèbre matricielle pour trouver les valeurs propres et les vecteurs propres.
Afficher/Masquer la réponse