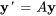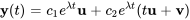6.8 Systèmes homogènes à coefficients constants : valeurs propres répétées
Dans cette section, nous explorons les solutions d’un système homogène à coefficients constants lorsque les valeurs propres de la matrice coefficient sont répétées. En particulier, nous rencontrons un défi unique lorsque la multiplicité algébrique d’une valeur propre (le nombre de fois où elle apparaît comme racine du polynôme caractéristique) dépasse sa multiplicité géométrique (le nombre de vecteurs propres linéairement indépendants qui lui sont associés). Cette différence nécessite une approche spécifique pour trouver toutes les solutions linéairement indépendantes nécessaires à une solution complète du système. Nous nous concentrons ici sur le cas où une valeur propre a une multiplicité algébrique de 2, mais une multiplicité géométrique de 1 seulement. Dans de telles situations, le concept de vecteurs propres généralisés devient crucial pour développer une solution complète.
Prenons un système homogène formulé comme suit :
où la matrice  a une valeur propre
a une valeur propre 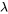 qui est répétée deux fois (elle a donc une multiplicité algébrique de 2).
qui est répétée deux fois (elle a donc une multiplicité algébrique de 2).
Théorème. Si une matrice 
 a une valeur propre
a une valeur propre 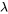 avec une multiplicité de 2, mais seulement un vecteur propre linéairement indépendant qui lui est associé (soit une multiplicité géométrique de 1), le système aura des solutions supplémentaires dérivées de vecteurs propres généralisés.
avec une multiplicité de 2, mais seulement un vecteur propre linéairement indépendant qui lui est associé (soit une multiplicité géométrique de 1), le système aura des solutions supplémentaires dérivées de vecteurs propres généralisés.
Trouver des vecteurs propres généralisés
Pour une valeur propre 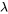 n’ayant qu’un vecteur propre standard indépendant
n’ayant qu’un vecteur propre standard indépendant 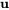 , il faut trouver un vecteur propre généralisé
, il faut trouver un vecteur propre généralisé 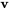 en résolvant l’équation
en résolvant l’équation
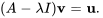
Ce vecteur propre généralisé 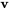 n’est pas une solution de
n’est pas une solution de 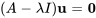 , mais satisfait l’équation ci-dessus.
, mais satisfait l’équation ci-dessus.
Construire la solution
La solution pour la valeur propre 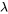 comporte des termes impliquant à la fois des vecteurs propres standard et des vecteurs propres généralisés. Les deux solutions sont linéairement indépendantes.
comporte des termes impliquant à la fois des vecteurs propres standard et des vecteurs propres généralisés. Les deux solutions sont linéairement indépendantes.
1. 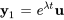 – associée au vecteur propre standard.
– associée au vecteur propre standard.
2. 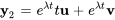 – associée au vecteur propre généralisé.
– associée au vecteur propre généralisé.
Solution générale du système
La solution générale du système présenté à la section 6.8.1 combine ces solutions.
où 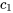 et
et 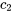 sont des constantes arbitraires.
sont des constantes arbitraires.
Résoudre le système d’équations différentielles avec les valeurs initiales données.
![bb"y'"=[(3,-1),(1,5)]bb"y", bb"y'"=[(3,-1),(1,5)]bb"y",](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/f09e42a2d3a103bd216148ef05508abb.png)
![bb"y"(0)=[(-3),(2)] bb"y"(0)=[(-3),(2)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/9d5af3b8317b5f0061190a7f371f27de.png)
Afficher/Masquer la solution
1. Il faut d’abord trouver les valeurs propres de la matrice coefficient  .
.
Le polynôme caractéristique de  est donné par
est donné par
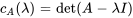
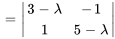
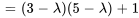
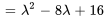
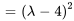
Le polynôme caractéristique 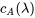 a une racine répétée. Ainsi,
a une racine répétée. Ainsi, 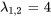 est la valeur propre de
est la valeur propre de  avec une multiplicité de 2.
avec une multiplicité de 2.
2. Pour trouver les vecteurs propres standard correspondants, il faut trouver la solution de l’équation 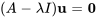 .
.
Pour 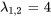 , on a
, on a
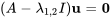
![=[(3-4,-1),(1,5-4)] =[(3-4,-1),(1,5-4)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/8247dc55ff8850e55bda3a67e5ea11ea.png)
![[(u_1),(u_2)]=[(0),(0)] [(u_1),(u_2)]=[(0),(0)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/e9b1c0442c96e0d85aaf52b869bdcbfa.png)
![[(-1,-1),(1,1) ] [(-1,-1),(1,1) ]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/87179f1e6e577c1c537729a392bd66ff.png)
![[(u_1),(u_2)]=[(0),(0)] [(u_1),(u_2)]=[(0),(0)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/e9b1c0442c96e0d85aaf52b869bdcbfa.png)
Pour résoudre le système, on forme la matrice augmentée et on la transforme en FERL au moyen d’opérations de ligne.
![[(-1,-1,|,0),(1,1,|,0) ]~ [(-1,-1,|,0),(1,1,|,0) ]~](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/89d3ec9c9b89ec2e21302fd39b0a0b9e.png)
![[(1,1,|,0),(0,0,|,0) ] [(1,1,|,0),(0,0,|,0) ]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/6985ba3fb517bc3844d2d5b03fc12f76.png)
Par conséquent, les vecteurs propres correspondant à 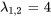 sont
sont ![bb"u"_1=t[(-1),(1)] bb"u"_1=t[(-1),(1)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/d3661f8ecd48fcb24ab4b5346714be3a.png) . En prenant
. En prenant 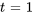 , un vecteur propre basique correspondant à
, un vecteur propre basique correspondant à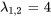 est
est 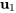
![=[(-1),(1)] =[(-1),(1)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/498f3f35f1049be0a6f6a50ecc2365de.png) .
.
3. Il faut trouver un vecteur propre généralisé 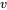 de façon à ce que
de façon à ce que
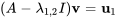
![[(-1,-1),(1,1) ] [(-1,-1),(1,1) ]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/87179f1e6e577c1c537729a392bd66ff.png)
![[(v_1),(v_2)]=[(-1),(1)] [(v_1),(v_2)]=[(-1),(1)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/5f843c22f13f1af47bff952d5ac2b2c0.png)
Pour résoudre le système, on forme la matrice augmentée et on la transforme en FERL au moyen d’opérations de ligne.
![[(-1,-1,|,-1),(1,1,|,1) ]~ [(-1,-1,|,-1),(1,1,|,1) ]~](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/21dca64a8e691e45f5a7a84c1d7c3f0b.png)
![[(1,1,|,1),(0,0,|,0) ] [(1,1,|,1),(0,0,|,0) ]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/190cf7fd84459a7212910f3b312d60e8.png)
La solution est ![bb"v"=[(1-t),(t)] bb"v"=[(1-t),(t)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/b9e16a3a08323bb0f1364d1c95497aa8.png) . En prenant
. En prenant 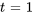 , un vecteur propre généralisé est
, un vecteur propre généralisé est 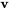
![=[(0),(1)] =[(0),(1)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/e766bfe89a28418ce539b45052b13de4.png) .
.
4. Une solution générale du système est donnée par l’équation présentée à la section 6.8.2.
![bb{y}(t)=c_1e^{4 t}[(-1),(1)]+ c_2e^(4t)(t[(-1),(1)] +[(0),(1)]) bb{y}(t)=c_1e^{4 t}[(-1),(1)]+ c_2e^(4t)(t[(-1),(1)] +[(0),(1)])](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/68d40aed5e09053099032023e6a3d1dc.png)
5. On applique les conditions initiales pour trouver les constantes 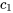 et
et 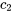 .
.
![bb"y"(0)=[(-3),(2)] bb"y"(0)=[(-3),(2)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/9d5af3b8317b5f0061190a7f371f27de.png)
![c_1[(-1),(1)]+ c_2[(0),(1)]= c_1[(-1),(1)]+ c_2[(0),(1)]=](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/1325071af8dffbd96307a8679c40226b.png)
![[(-3),(2)] [(-3),(2)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/c4b2f4a86177bce6838c8835fd57713b.png)
On obtient ainsi un système de deux équations à deux inconnues.
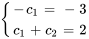
En résolvant le système, on obtient
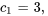
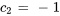
La solution du problème de valeur initiale est donc
![bb{y}(t)=3e^{4 t}[(-1),(1)]-e^(4t)(t[(-1),(1)] +[(0),(1)]) bb{y}(t)=3e^{4 t}[(-1),(1)]-e^(4t)(t[(-1),(1)] +[(0),(1)])](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/ea1708112a443d7544f7d5434fd54e07.png)
Prenons un exemple
Résoudre le système d’équations différentielles avec les valeurs initiales données.
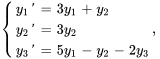
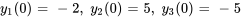
Afficher/Masquer la solution
1. On exprime d’abord le PVI dans la notation matricielle.
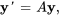
![bb(y)(0)=[(-2),(5),(-5)] bb(y)(0)=[(-2),(5),(-5)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/e44bcc9e356b507053b731e0eea55f2c.png)
où ![A=[(3,1,0),(0,3,0),(5,-1,-2) ] A=[(3,1,0),(0,3,0),(5,-1,-2) ]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/b2bf9747e24ba18aaa67d971dd42f7e6.png) .
.
2. On trouve les valeurs propres de la matrice coefficient  .
.
Le polynôme caractéristique de  est donné par
est donné par
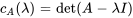
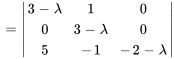
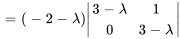
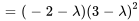
Les valeurs propres sont 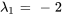 avec une multiplicité de 1 et
avec une multiplicité de 1 et 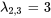 avec une multiplicité de 2.
avec une multiplicité de 2.
3. Pour trouver les vecteurs propres standard correspondants, on résout 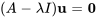 .
.
Pour 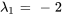 , on a
, on a
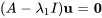
![=[(5,1,0),(0,5,0),(5,-1,0) ] =[(5,1,0),(0,5,0),(5,-1,0) ]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/7bbbeeb054bbab5dbb39381c9f63b20e.png)
![[(u_1),(u_2),(u_3)]=[(0),(0),(0)] [(u_1),(u_2),(u_3)]=[(0),(0),(0)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/6dc2224125889777fa8b76b924f340f7.png)
Pour résoudre le système, on forme la matrice augmentée et on la transforme en FERL au moyen d’opérations de ligne.
![[(5,1,0),(0,5,0),(5,-1,0) ]~ [(5,1,0),(0,5,0),(5,-1,0) ]~](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/d5d68d6c265aa2eb713dec18f16b5502.png)
![[(1,0,0),(0,1,0),(0,0,0) ] [(1,0,0),(0,1,0),(0,0,0) ]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/237f7e45de8bc0cc9c3b35a266fe5869.png)
Par conséquent, les vecteurs propres correspondant à 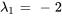 sont
sont ![bb"u"_1=t[(0),(0),(1)] bb"u"_1=t[(0),(0),(1)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/aee77b941e55c29fd2d589cef79e986c.png) . En prenant
. En prenant 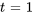 , un vecteur propre basique correspondant à
, un vecteur propre basique correspondant à 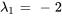 est
est 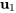
![=[(0),(0),(1)] =[(0),(0),(1)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/c0aa76e22e9821ce06e970227de29f81.png) .
.
Pour 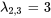 , on a
, on a
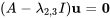
![=[(0,1,0),(0,0,0),(5,-1,-5) ] =[(0,1,0),(0,0,0),(5,-1,-5) ]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/516716725cce4cd72d787b0505947b3f.png)
![[(u_1),(u_2),(u_3)]=[(0),(0),(0)] [(u_1),(u_2),(u_3)]=[(0),(0),(0)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/6dc2224125889777fa8b76b924f340f7.png)
Pour résoudre le système, on forme la matrice augmentée et on la transforme en FERL au moyen d’opérations de ligne.
![[(0,1,0,|,0),(0,0,0,|,0) ,(5,-1,-5,|,0) ]~ [(0,1,0,|,0),(0,0,0,|,0) ,(5,-1,-5,|,0) ]~](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/3f8f5215753906cc817569ef43ee250a.png)
![[(1,0,-1,|,0),(0,1,0,|,0) ,(0,0,0,|,0) ] [(1,0,-1,|,0),(0,1,0,|,0) ,(0,0,0,|,0) ]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/95f4ff07490d82fe6bd8b389cb5c4594.png)
Par conséquent, les vecteurs propres correspondant à 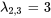 sont
sont ![bb"u"_2=t[(1),(0),(1)] bb"u"_2=t[(1),(0),(1)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/b8f0a7a1c3edc5d1a59859d658d533ab.png) . En prenant
. En prenant 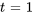 , un vecteur propre basique correspondant à
, un vecteur propre basique correspondant à 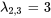 est
est 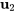
![=[(1),(0),(1)] =[(1),(0),(1)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/a3b03aef73c51b9466daa1293f7663b7.png) .
.
Pour 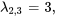 la multiplicité géométrique est de 1, et donc inférieure à la multiplicité algébrique (qui est de 2). Cela signifie que la dimension de l’espace propre associé à
la multiplicité géométrique est de 1, et donc inférieure à la multiplicité algébrique (qui est de 2). Cela signifie que la dimension de l’espace propre associé à 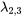 est égale à 1 (tous les vecteurs propres sont traversés par le seul vecteur
est égale à 1 (tous les vecteurs propres sont traversés par le seul vecteur 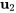 ).
).
4. On doit donc trouver un vecteur généralisé 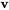 de façon à ce que
de façon à ce que
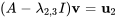
![[(0,1,0),(0,0,0),(5,-1,-5) ] [(v_1),(v_2),(v_3)]=[(1),(0),(1)] [(0,1,0),(0,0,0),(5,-1,-5) ] [(v_1),(v_2),(v_3)]=[(1),(0),(1)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/d2a786e23776770c5213297bea277cd7.png)
Pour résoudre le système, on forme la matrice augmentée et on la transforme en FERL au moyen d’opérations de ligne.
![[(0,1,0,|,1),(0,0,0,|,0),(5,-1,-5,|,1) ]~ [(0,1,0,|,1),(0,0,0,|,0),(5,-1,-5,|,1) ]~](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/82aef669b24d903020d3a3f74d69f3dd.png)
![[(1,0,-1,|,2/5),(0,1,0,|,1),(0,0,0,|,0) ] [(1,0,-1,|,2/5),(0,1,0,|,1),(0,0,0,|,0) ]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/4412f7433061a526ab52aa72eef62889.png)
La solution est ![bb"v"=[(2/5+t),(1),(t)] bb"v"=[(2/5+t),(1),(t)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/72b882fc1ec0da9b5810e674fafb5c36.png) . En prenant
. En prenant 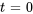 , un vecteur propre généralisé est
, un vecteur propre généralisé est 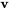
![=[(2/5),(1),(0)] =[(2/5),(1),(0)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/b955c6765a6cd398e1306e85f9c2a25a.png) .
.
5. Trois solutions linéairement indépendantes du système sont
– Pour 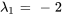 et le vecteur propre standard
et le vecteur propre standard 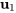 :
:
![bb(y)_1=e^(-2t)[(0),(0),(1)] bb(y)_1=e^(-2t)[(0),(0),(1)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/4abaaacd8656066b267f67dcce668e05.png)
– Pour 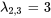 et le vecteur propre standard
et le vecteur propre standard 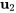 :
:
![bb(y)_2=e^(3t)[(1),(0),(1)] bb(y)_2=e^(3t)[(1),(0),(1)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/f05261947112b1988ffee68fc9b14a28.png)
– Pour 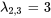 et un vecteur propre généralisé
et un vecteur propre généralisé 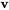 :
:
![bb(y)_3=e^(3t)(t[(1),(0),(1)]+[(2//5),(1),(0)]) bb(y)_3=e^(3t)(t[(1),(0),(1)]+[(2//5),(1),(0)])](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/b4af683251a3c94142fbd79c1e4d0194.png)
6. Par conséquent, une solution générale au système est donnée par la combinaison linéaire des solutions ci-dessus :
![bb(y)(t)=c_1e^(-2t)[(0),(0),(1)] + bb(y)(t)=c_1e^(-2t)[(0),(0),(1)] +](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/945cfdb1295dc89d21dd750dc302d48d.png)
![c_2e^(3t)[(1),(0),(1)]+ c_2e^(3t)[(1),(0),(1)]+](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/3dde38e3cd25ff1c339753ac96f1292a.png)
![c_3e^(3t)(t[(1),(0),(1)]+[(2//5),(1),(0)]) c_3e^(3t)(t[(1),(0),(1)]+[(2//5),(1),(0)])](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/ae0cedbb8fa81a7f83b76188cbf67f59.png)
7. On applique maintenant les conditions initiales pour trouver les constantes.
![bb(y)(0)=[(-2),(5),(-5)] bb(y)(0)=[(-2),(5),(-5)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/e44bcc9e356b507053b731e0eea55f2c.png)
![c_1[(0),(0),(1)] + c_1[(0),(0),(1)] +](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/97261189dea181f651175d2abde86124.png)
![c_2[(1),(0),(1)]+ c_2[(1),(0),(1)]+](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/01509b95d86b8d2e953af0186fb84c63.png)
![c_3[(2//5),(1),(0)]= c_3[(2//5),(1),(0)]=](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/dcd4240587a81d6ea50857ae7cdb5f85.png)
![[(-2),(5),(-5)] [(-2),(5),(-5)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/dd3b2a8606ef2ec33b2507dcef810536.png)
On obtient ainsi un système de trois équations à trois inconnues.
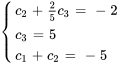
En résolvant le système, on obtient


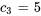
La solution du problème de valeur initiale est donc
![bb(y)(t)=-e^(-2t)[(0),(0),(1)]- bb(y)(t)=-e^(-2t)[(0),(0),(1)]-](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/0146d79f7b2f17ef6685ac93601d5448.png)
![4e^(3t)[(1),(0),(1)]+ 4e^(3t)[(1),(0),(1)]+](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/ff276acedeadcd0ad5c2b6a7ad6f58ea.png)
![5e^(3t)(t[(1),(0),(1)]+[(2//5),(1),(0)]) 5e^(3t)(t[(1),(0),(1)]+[(2//5),(1),(0)])](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/36c05bc8a689b208a7c7d1a6de74e1ca.png)
Prenons un exemple
Section 6.8 Exercices
- Résous le système d’équations différentielles
![bb"y"'=[(-3,1),(-1,-5)] bb"y" bb"y"'=[(-3,1),(-1,-5)] bb"y"](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/360bacacdad5eaaaa9b98c9417d59726.png) ,
, ![bb"y"(t)=[(9 ),(-13)] bb"y"(t)=[(9 ),(-13)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/8cf9c79b981e6b3872e75309bfd5e8b1.png)
Afficher/Masquer la réponse
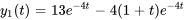
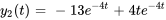
- Résous le système d’équations différentielles
![bb"y"'=[(-6,2),(-2,-10)] bb"y" bb"y"'=[(-6,2),(-2,-10)] bb"y"](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/3c1467fceeec68123bfc6d912d3c15f5.png) ,
, ![bb"y"(t)=[(-14 ),(-26)] bb"y"(t)=[(-14 ),(-26)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/519c2409f0f19e702bba37f725d57eb6.png)
Afficher/Masquer la réponse

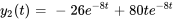
- Résous le système d’équations différentielles
![bb"y"'=[(2,1,0),(0,2,0),(4,-3,-1)] bb"y" bb"y"'=[(2,1,0),(0,2,0),(4,-3,-1)] bb"y"](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/d0b47dfe5b4798c677412f7812b71f09.png) ,
, ![bb"y"(t)=[(-9 ),(-18),(27)] bb"y"(t)=[(-9 ),(-18),(27)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/1bc5a1103f368802b5b2676de35e5bf8.png)
Afficher/Masquer la réponse
![bb(y)(t)=13e^(-t)[(0),(0),(1)]+ bb(y)(t)=13e^(-t)[(0),(0),(1)]+](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/91ec65e901de3762c0299edb6c1fc0bf.png)
![7/2e^(2t)[(3),(0),(4)]- 7/2e^(2t)[(3),(0),(4)]-](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/af0552ff754212501433197e93f4036e.png)
![6e^(2t)(t[(3),(0),(4)]+[(13//4),(3),(0)]) 6e^(2t)(t[(3),(0),(4)]+[(13//4),(3),(0)])](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/0fcc5a578caef9b710c7224fd8d6ebcc.png)