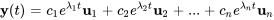6.6 Systèmes homogènes à coefficients constants : valeurs propres réelles
À la section 6.5, vous avons vu que les solutions de systèmes homogènes à coefficients constants
présentent la forme
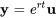
où 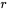 est une valeur propre et
est une valeur propre et 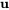 est le vecteur propre correspondant de la matrice coefficient
est le vecteur propre correspondant de la matrice coefficient  .
.
Dans cette section, nous nous intéressons au cas où les valeurs propres d’une matrice  sont distinctes et réelles.
sont distinctes et réelles.
Théorème : si une matrice 
 a
a 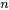 valeurs propres réelles et distinctes
valeurs propres réelles et distinctes 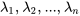 et si
et si 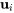 est un vecteur propre associé à la valeur propre
est un vecteur propre associé à la valeur propre 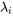 , alors les vecteurs
, alors les vecteurs 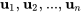 sont linéairement indépendants.
sont linéairement indépendants.
Dans ce contexte, les solutions de chaque valeur propre prennent la forme 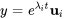 . Collectivement, l’ensemble
. Collectivement, l’ensemble 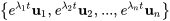 forme un ensemble fondamental de solutions pour le système homogène présenté à la section 6.6.1.
forme un ensemble fondamental de solutions pour le système homogène présenté à la section 6.6.1.
Par conséquent, la solution générale peut être exprimée comme une combinaison linéaire de ces solutions individuelles.
où 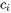 est une constante arbitraire.
est une constante arbitraire.
Trouver la solution générale de
![bb"y"'=[(-6,-3),(1,-2)]bb"y" bb"y"'=[(-6,-3),(1,-2)]bb"y"](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/38c61dc42f329494306f5698e5b7cdcd.png)
Afficher/Masquer la solution
1. Il faut d’abord trouver les valeurs propres de la matrice coefficient  .
.
Le polynôme caractéristique de  est donné par
est donné par
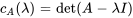
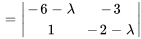
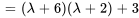
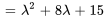
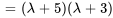
Les racines de 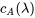 , à savoir
, à savoir 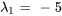 et
et 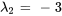 , sont les valeurs propres de
, sont les valeurs propres de  .
.
2. Ensuite, pour trouver les vecteurs propres correspondants, il faut trouver la solution à l’équation 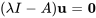 pour chaque valeur propre.
pour chaque valeur propre.
Pour 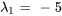 , on a
, on a
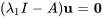
![[(-5+6,3),(-1,-5+2) ] [(-5+6,3),(-1,-5+2) ]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/fd4deaa946c17175501bf60f9a18aed9.png)
![[(u_1),(u_2)]=[(0),(0)] [(u_1),(u_2)]=[(0),(0)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/e9b1c0442c96e0d85aaf52b869bdcbfa.png)
![[(1,3),(-1,-3) ] [(1,3),(-1,-3) ]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/d38c9ba6a5327c7e4de0f4489c470f09.png)
![[(u_1),(u_2)]=[(0),(0)] [(u_1),(u_2)]=[(0),(0)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/e9b1c0442c96e0d85aaf52b869bdcbfa.png)
Par conséquent, les vecteurs propres correspondant à 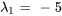 sont
sont ![bb"u"_1=t[(-3),(1)] bb"u"_1=t[(-3),(1)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/e4da5d17db48a23bea55c28c22904bc9.png) pour
pour 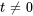 . En prenant
. En prenant 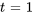 , un vecteur propre basique correspondant à
, un vecteur propre basique correspondant à 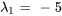 est
est 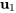
![=[(-3),(1)] =[(-3),(1)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/be2f3302a914133956a21f686e379aa2.png) .
.
Pour 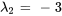 , on a
, on a
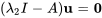
![[(-3+6,3),(-1,-3+2) ] [(-3+6,3),(-1,-3+2) ]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/a77db9161968655810f9900bc9fff30a.png)
![[(u_1),(u_2)]=[(0),(0)] [(u_1),(u_2)]=[(0),(0)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/e9b1c0442c96e0d85aaf52b869bdcbfa.png)
![[(3,3),(-1,-1) ] [(3,3),(-1,-1) ]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/f3713f46c0713d57dafc682bb73b40ed.png)
![[(u_1),(u_2)]=[(0),(0)] [(u_1),(u_2)]=[(0),(0)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/e9b1c0442c96e0d85aaf52b869bdcbfa.png)
Pour résoudre le système, on forme la matrice augmentée et on la transforme en FERL au moyen d’opérations de ligne.
![[(3,3,|,0),(-1,-1,|,0) ]~ [(3,3,|,0),(-1,-1,|,0) ]~](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/94f8def0ebc64f080d18d0826164df4f.png)
![[(1,1,|,0),(0,0,|,0) ] [(1,1,|,0),(0,0,|,0) ]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/6985ba3fb517bc3844d2d5b03fc12f76.png)
Par conséquent, les vecteurs propres correspondant à 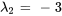 sont
sont ![bb"u"_2=t[(-1),(1)] bb"u"_2=t[(-1),(1)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/d7edd41fab71b4c250b10a63da2cf820.png) pour
pour 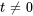 . En prenant
. En prenant 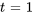 , un vecteur propre basique correspondant à
, un vecteur propre basique correspondant à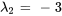 est
est 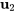
![=[(-1),(1)] =[(-1),(1)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/498f3f35f1049be0a6f6a50ecc2365de.png) .
.
3. Une solution générale du système est donnée par l’équation présentée à la section 6.6.2.
![bb"y"(t)=c_1e^(-5t) [(-3),(1)]+c_2 e^(-3t) [(-1),(1)] bb"y"(t)=c_1e^(-5t) [(-3),(1)]+c_2 e^(-3t) [(-1),(1)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/2bdc07a3d8b0e6449fd9c9ab4cb433ab.png)
Prenons un exemple
Résoudre le système d’équations différentielles avec les valeurs initiales données.
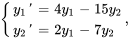
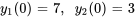
Afficher/Masquer la solution
1. On exprime d’abord le système dans la notation matricielle.
![bb"y"'=[(4,-15),(2,-7) ]bb"y", bb"y"'=[(4,-15),(2,-7) ]bb"y",](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/6888113509412f74f9b600c4920eb89b.png)
![bb"y"(0)=[(7),(3)] bb"y"(0)=[(7),(3)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/543ee09260447a166e588c6bc4e775f2.png)
2. Ensuite, on trouve les valeurs propres de  .
.
Le polynôme caractéristique de la matrice coefficient  est donné par
est donné par
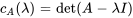
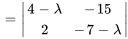

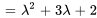
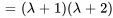
Les racines de 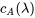 , à savoir
, à savoir 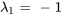 et
et 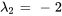 , sont les valeurs propres de
, sont les valeurs propres de  .
.
3. On trouve ensuite les vecteurs propres correspondants.
Pour 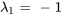 , on a
, on a
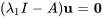
![[(4+1,-15),(2,-7+1) ] [(4+1,-15),(2,-7+1) ]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/c6e4f7284ad4e9979fb1b0af976cdd55.png)
![[(u_1),(u_2)]=[(0),(0)] [(u_1),(u_2)]=[(0),(0)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/e9b1c0442c96e0d85aaf52b869bdcbfa.png)
![[(5,-15),(2,-6) ] [(5,-15),(2,-6) ]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/ccbf25f2e3dca99aa6b0eaa43b12706e.png)
![[(u_1),(u_2)]=[(0),(0)] [(u_1),(u_2)]=[(0),(0)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/e9b1c0442c96e0d85aaf52b869bdcbfa.png)
Pour résoudre le système, on forme la matrice augmentée et on la transforme en FERL au moyen d’opérations de ligne.
![[(5,-15,|,0),(2,-6,|,0) ]~ [(5,-15,|,0),(2,-6,|,0) ]~](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/bc8d57ed8916e2134a539f0787410123.png)
![[(1,-3,|,0),(0,0,|,0) ] [(1,-3,|,0),(0,0,|,0) ]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/8dff248d0a39c59e481fff56e75ed5d7.png)
Par conséquent, les vecteurs propres correspondant à 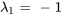 sont
sont ![bb"u"_1=t[(3),(1)] bb"u"_1=t[(3),(1)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/3e5e54dc66c7af503627d7e2fe951835.png) pour
pour 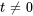 . En prenant
. En prenant 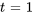 , un vecteur propre basique correspondant à
, un vecteur propre basique correspondant à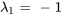 est
est 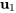
![=[(3),(1)] =[(3),(1)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/45e9e12108afcbd1818417640251c611.png) .
.
Pour 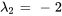 , on a
, on a
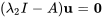
![[(4+2,-15),(2,-7+2) ] [(4+2,-15),(2,-7+2) ]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/c4fed569316fb5d506cce7c8942e7617.png)
![[(u_1),(u_2)]=[(0),(0)] [(u_1),(u_2)]=[(0),(0)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/e9b1c0442c96e0d85aaf52b869bdcbfa.png)
![[(6,-15),(2,-5) ] [(6,-15),(2,-5) ]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/0cc9eeaf193b444e4f54c5eff1457686.png)
![[(u_1),(u_2)]=[(0),(0)] [(u_1),(u_2)]=[(0),(0)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/e9b1c0442c96e0d85aaf52b869bdcbfa.png)
Pour résoudre le système, on forme la matrice augmentée et on la transforme en FERL au moyen d’opérations de ligne.
![[(6,-15,|,0),(2,-5,|,0) ]~ [(6,-15,|,0),(2,-5,|,0) ]~](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/987b097e57a9c89d1360b0343fa801ca.png)
![[(1,-5/2,|,0),(0,0,|,0) ] [(1,-5/2,|,0),(0,0,|,0) ]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/a81aa9b57eaef4dffb2a967c7a9321e1.png)
Par conséquent, les vecteurs propres correspondant à 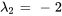 sont
sont ![bb"u"_2=t[(5/2),(1)] bb"u"_2=t[(5/2),(1)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/5003be2be2b2ca9a733b01d5abc6407b.png) pour
pour 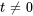 . En prenant
. En prenant 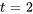 , un vecteur propre basique correspondant à
, un vecteur propre basique correspondant à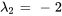 est
est 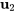
![=[(5),(2)] =[(5),(2)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/0ac20742c10b8d51093885b4058a4542.png) .
.
4. Une solution générale du système est donnée par l’équation présentée à la section 6.6.2.
![bb"y"(t)=c_1e^(-t) [(3),(1)]+c_2 e^(-2t) [(5),(2)] bb"y"(t)=c_1e^(-t) [(3),(1)]+c_2 e^(-2t) [(5),(2)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/e5595c165b6d608e0dd5c0d3262f6084.png)
5. Enfin, on applique les conditions initiales pour trouver les constantes 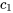 et
et 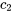 .
.
![bb"y"(0)=[(7),(3)] bb"y"(0)=[(7),(3)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/543ee09260447a166e588c6bc4e775f2.png)
![c_1e^(0) [(3),(1)]+c_2 e^(0) [(5),(2)]=[(7),(3)] c_1e^(0) [(3),(1)]+c_2 e^(0) [(5),(2)]=[(7),(3)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/e640c171996d8cbe0a6303e4efc35844.png)
![[(3c_1+5c_2),(c_1+2c_2)]= [(3c_1+5c_2),(c_1+2c_2)]=](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/d36f9d592255261a1ff35b51afb34e7a.png)
![[(7),(3)] [(7),(3)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/e11f12523a31660dd0be9e941954d2f7.png)
On obtient ainsi un système de deux équations à deux inconnues.
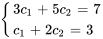
En résolvant le système, on trouve

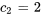
La solution du problème de valeur initiale est donc
![bb"y"(t)=-e^(-t) [(3),(1)]+2 e^(-2t) [(5),(2)] bb"y"(t)=-e^(-t) [(3),(1)]+2 e^(-2t) [(5),(2)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/3245be839a3e3c9dcfaf82f1c378f6ff.png)
Prenons un exemple
Résoudre le système d’équations différentielles avec les valeurs initiales données.
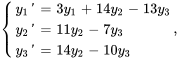
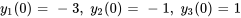
Afficher/Masquer la solution
1. On exprime d’abord le système dans la notation matricielle.
![bb"y"'=[(3,14,-13),(0,11,-7),(0,14,-10) ]bb"y", bb"y"'=[(3,14,-13),(0,11,-7),(0,14,-10) ]bb"y",](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/2bf68d5c7004f34f0ad99eb61d8b79fd.png)
![bb"y"(0)=[(-3),(-1),(1)] bb"y"(0)=[(-3),(-1),(1)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/5b0af8aebe1f0b853bec18a265e2845e.png)
2. Il faut d’abord trouver les valeurs propres de la matrice coefficient  .
.
Le polynôme caractéristique de  est donné par
est donné par
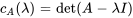
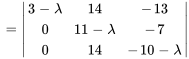
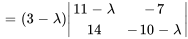
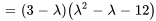
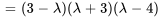
Les racines de 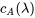 , à savoir
, à savoir 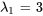 ,
, 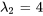 , et
, et 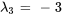 , sont les valeurs propres de
, sont les valeurs propres de  .
.
3. On trouve ensuite les vecteurs propres correspondants.
Pour 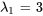 , on a
, on a
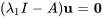
![=[(0,14,-13),(0,8,-7),(0,14,-13)] =[(0,14,-13),(0,8,-7),(0,14,-13)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/cd5fccd0048d80d02286f0ac117c9b26.png)
![[(u_1),(u_2),(u_3)]=[(0),(0),(0)] [(u_1),(u_2),(u_3)]=[(0),(0),(0)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/6dc2224125889777fa8b76b924f340f7.png)
Pour résoudre le système, on forme la matrice augmentée et on la transforme en FERL au moyen d’opérations de ligne.
![[(0,14,-13,|,0),(0,8,-7,|,0),(0,14,-13,|,0)]~ [(0,14,-13,|,0),(0,8,-7,|,0),(0,14,-13,|,0)]~](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/320c4c73672d92f46818b2d2ada01b6e.png)
![[(0,1,0,|,0),(0,0,1,|,0),(0,0,0,|,0)] [(0,1,0,|,0),(0,0,1,|,0),(0,0,0,|,0)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/bbc94483e774662380e69eaf22cea584.png)
Par conséquent, les vecteurs propres correspondant à 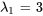 sont
sont ![bb"u"_1=t[(1),(0),(0)] bb"u"_1=t[(1),(0),(0)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/ad39fa631be7613d5c978895aacdd577.png) pour
pour 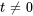 . En prenant
. En prenant 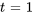 , un vecteur propre basique correspondant à
, un vecteur propre basique correspondant à 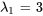 est
est 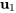
![=[(1),(0),(0)] =[(1),(0),(0)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/b26f36a02ead78466df895fa6d4eef79.png) .
.
Pour 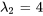 , on a
, on a
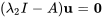
![=[(-1,14,-13),(0,7,-7),(0,14,-14)] =[(-1,14,-13),(0,7,-7),(0,14,-14)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/8d5bd90017cc902da2275ea9b324171e.png)
![[(u_1),(u_2),(u_3)]=[(0),(0),(0)] [(u_1),(u_2),(u_3)]=[(0),(0),(0)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/6dc2224125889777fa8b76b924f340f7.png)
Pour résoudre le système, on forme la matrice augmentée et on la transforme en FERL au moyen d’opérations de ligne.
![[(-1,14,-13),(0,7,-7),(0,14,-14)]~ [(-1,14,-13),(0,7,-7),(0,14,-14)]~](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/a1e532665395cf1da466168b7ea37f1f.png)
![[(1,0,-1),(0,1,-1),(0,0,0)] [(1,0,-1),(0,1,-1),(0,0,0)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/04e4fbb13c43b87dfbca2d28f28f5d84.png)
Ainsi, les vecteurs propres correspondant à 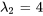 sont
sont ![bb"u"_2=t[(1),(1),(1)] bb"u"_2=t[(1),(1),(1)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/4916f6370cff8266fb8130aed43f6bf6.png) pour
pour 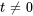 . En prenant
. En prenant 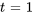 , un vecteur propre basique correspondant à
, un vecteur propre basique correspondant à 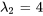 est
est 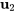
![=[(1),(1),(1)] =[(1),(1),(1)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/05f4b8b70a797f95189a83dbb0c814a2.png) .
.
Pour 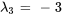 , on a
, on a
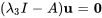
![=[(6,14,-13),(0,14,-7),(0,14,-7)] =[(6,14,-13),(0,14,-7),(0,14,-7)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/1b39752484d05a7cdfad01315f495eed.png)
![[(u_1),(u_2),(u_3)]=[(0),(0),(0)] [(u_1),(u_2),(u_3)]=[(0),(0),(0)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/6dc2224125889777fa8b76b924f340f7.png)
Pour résoudre le système, on forme la matrice augmentée et on la transforme en FERL au moyen d’opérations de ligne.
![[(6,14,-13),(0,14,-7),(0,14,-7)]~ [(6,14,-13),(0,14,-7),(0,14,-7)]~](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/03b7bfd39997e75ed74b4cb7dbf4adb5.png)
![[(1,0,-1),(0,1,-1/2),(0,0,0)] [(1,0,-1),(0,1,-1/2),(0,0,0)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/f08bfdcfdac7d9da129eef558c26808e.png)
Par conséquent, les vecteurs propres correspondant à 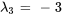 sont
sont ![bb"u"_3=t[(1),(1/2),(1)] bb"u"_3=t[(1),(1/2),(1)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/dd7de75c48fd70f1a46235d0447cadde.png) pour
pour 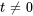 . En prenant
. En prenant 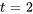 , un vecteur propre basique correspondant à
, un vecteur propre basique correspondant à 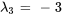 est
est 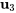
![=[(2),(1),(2)] =[(2),(1),(2)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/ee62b54110edb439c009de8236ec464f.png) .
.
4. Une solution générale du système est donnée par l’équation présentée à la section 6.6.2.
![bb"y"(t)=c_1e^(3t) [(1),(0),(0)]+c_2 e^(4t) [(1),(1),(1)]+c_3e^(-3t)[(2),(1),(2)] bb"y"(t)=c_1e^(3t) [(1),(0),(0)]+c_2 e^(4t) [(1),(1),(1)]+c_3e^(-3t)[(2),(1),(2)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/7aaefd66f914840d7a488a6c5b4278bb.png)
5. Enfin, on applique les conditions initiales pour trouver les constantes 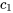 ,
, 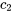 et
et 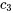 .
.
![bb"y"(0)=[(-3),(-1),(1)] bb"y"(0)=[(-3),(-1),(1)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/5b0af8aebe1f0b853bec18a265e2845e.png)
![c_1e^0 [(1),(0),(0)]+c_2 e^0 [(1),(1),(1)]+c_3e^0[(2),(1),(2)] =[(-3),(-1),(1)] c_1e^0 [(1),(0),(0)]+c_2 e^0 [(1),(1),(1)]+c_3e^0[(2),(1),(2)] =[(-3),(-1),(1)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/3524223183a6cea73c3d5689278eb478.png)
On obtient ainsi un système de trois équations à trois inconnues.
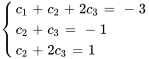
En résolvant le système, on trouve


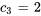
La solution du problème de valeur initiale est donc
![bb"y"(t)=-4e^(3t) [(1),(0),(0)]-3 e^(4t) [(1),(1),(1)]+2e^(-3t)[(2),(1),(2)] bb"y"(t)=-4e^(3t) [(1),(0),(0)]-3 e^(4t) [(1),(1),(1)]+2e^(-3t)[(2),(1),(2)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/c3802243b270ce109ab6b1aae5299474.png)
Prenons un exemple
À la section 6.4, nous avons vu comment les équations différentielles linéaires d’ordre supérieur peuvent être converties en systèmes d’équations linéaires du premier ordre. Cette transformation, associée à la méthode matricielle, offre plusieurs avantages, notamment une meilleure organisation du problème et une facilité de calcul. Bien que cette approche ne soit pas toujours plus courte que la méthode du polynôme caractéristique présentée à la section 3.2, en particulier pour résoudre des équations différentielles homogènes du second ordre à coefficients constants, il est utile de comprendre ce processus. Pour illustrer son application, prenons un exemple.
Convertir l’équation différentielle donnée en un système linéaire du premier ordre et trouver la solution.

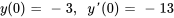
Afficher/Masquer la solution
a. Convertir l’équation en un système :
1a. Introduire une nouvelle variable 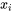 :
:
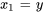
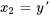
2a. Exprimer les dérivées en différenciant les équations ci-dessus et réarranger l’équation différentielle originale afin d’isoler 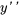 :
:
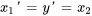
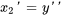
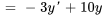

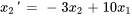
On exprime aussi les conditions initiales par rapport aux nouvelles variables :
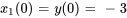
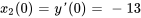
3a. Le système d’équations du premier ordre est donc
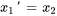
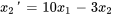
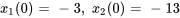
1b. On exprime le système sous forme matricielle.
![bb"x"'=[(0,1),(10,-3) ]bb"x", bb"x"'=[(0,1),(10,-3) ]bb"x",](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/d50b65c563d93bd6b4c601dcab133c0c.png)
![bb"x"(0)=[(-3),(-13)] bb"x"(0)=[(-3),(-13)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/50755826da3437fdd59c07ac0b49b87c.png)
2b. Il faut d’abord trouver les valeurs propres de la matrice coefficient  .
.
Le polynôme caractéristique de  est donné par
est donné par
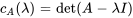
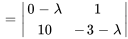
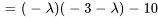
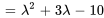
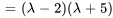
Les racines de 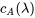 , à savoir
, à savoir 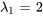 et
et 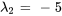 , sont les valeurs propres de
, sont les valeurs propres de  .
.
3b. On trouve ensuite les vecteurs propres correspondants.
Pour 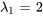 , on a
, on a
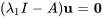
![[(-2,1),(10,-5) ] [(-2,1),(10,-5) ]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/5d186004c5d7e64f66aaab55aa11d43c.png)
![[(u_1),(u_2)]=[(0),(0)] [(u_1),(u_2)]=[(0),(0)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/e9b1c0442c96e0d85aaf52b869bdcbfa.png)
Pour résoudre le système, on forme la matrice augmentée et on la transforme en FERL au moyen d’opérations de ligne.
![[(-2,1,|,0),(10,-5,|,0) ]~ [(-2,1,|,0),(10,-5,|,0) ]~](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/9c6c52cac731b8f6e98ab0b27ca1e870.png)
![[(1,-1/2,|,0),(0,0,|,0) ] [(1,-1/2,|,0),(0,0,|,0) ]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/9e8213c71e8db6ee33881c84287f43db.png)
Par conséquent, les vecteurs propres correspondant à 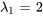 sont
sont ![bb"u"_1=t[(1/2),(1)] bb"u"_1=t[(1/2),(1)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/a08c79201a92bcd64c1fb54c5e642814.png) pour
pour 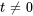 . En prenant
. En prenant 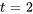 , un vecteur propre basique est
, un vecteur propre basique est 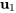
![=[(1),(2)] =[(1),(2)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/6fe213f529670406fdd238c414a350ee.png) .
.
Pour 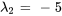 , on a
, on a
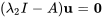
![[(5,1),(10,2) ] [(5,1),(10,2) ]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/4f63244685ddfdd173ed8e5c566b638f.png)
![[(u_1),(u_2)]=[(0),(0)] [(u_1),(u_2)]=[(0),(0)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/e9b1c0442c96e0d85aaf52b869bdcbfa.png)
Pour résoudre le système, on forme la matrice augmentée et on la transforme en FERL au moyen d’opérations de ligne.
![[(5,1,|,0),(10,2,|,0) ]~ [(5,1,|,0),(10,2,|,0) ]~](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/24d68543552efe12c45281b3c8559a99.png)
![[(1,1/5,|,0),(0,0,|,0) ] [(1,1/5,|,0),(0,0,|,0) ]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/87a554c05e58a18cd8d2a5d8e0078bd7.png)
Par conséquent, les vecteurs propres correspondant à 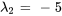 sont
sont ![bb"u"_2=t[(-1/5),(1)] bb"u"_2=t[(-1/5),(1)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/3c4f6a9195bb454cf3318c7ab9f58942.png) pour
pour 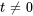 . En prenant
. En prenant 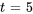 , un vecteur propre basique est
, un vecteur propre basique est 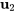
![=[(-1),(5)] =[(-1),(5)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/2e9a58ece306bafbb03a88f31cf55f9d.png) .
.
4b. Une solution générale du système est donnée par l’équation présentée à la section 6.6.2.
![bb"x"(t)=c_1e^(2t) [(1),(2)]+c_2 e^(-5t) [(-1),(5)] bb"x"(t)=c_1e^(2t) [(1),(2)]+c_2 e^(-5t) [(-1),(5)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/f58eb59ed722908eefca8ff516fccc15.png)
5b. On applique les conditions initiales pour trouver les constantes 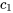 et
et 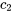 .
.
![bb"x"(0)=[(-3),(-13)] bb"x"(0)=[(-3),(-13)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/50755826da3437fdd59c07ac0b49b87c.png)
![c_1e^(0) [(1),(2)]+c_2 e^(0) [(-1),(5)]=[(-3),(-13)] c_1e^(0) [(1),(2)]+c_2 e^(0) [(-1),(5)]=[(-3),(-13)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/856d900f952fb254defb3bfb5766508a.png)
![[(c_1-c_2),(2c_1+5c_2)]= [(c_1-c_2),(2c_1+5c_2)]=](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/7ac7a80f0c4c60928d5112d74b6baf55.png)
![[(-3),(-13)] [(-3),(-13)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/70a5d4386143b4769e9edcaed63485db.png)
On obtient ainsi un système de deux équations à deux inconnues.
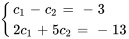
En résolvant le système, on trouve

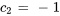
La solution du problème de valeur initiale est donc
![bb"x"(t)=-4e^(2t) [(1),(2)]- e^(-5t) [(-1),(5)] bb"x"(t)=-4e^(2t) [(1),(2)]- e^(-5t) [(-1),(5)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/c52efe82042ca1b2134b55182f727bc2.png)
c. Déterminer la solution de l’équation originale
Étant donné que ![bb"x"(t)=[(x_1),(x_2)]=[(y),(y')] bb"x"(t)=[(x_1),(x_2)]=[(y),(y')]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/f699f8809574fc72b0cb9cf2be9e4322.png) , on voit que la solution de l’équation différentielle du second ordre d’origine
, on voit que la solution de l’équation différentielle du second ordre d’origine 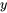 est la ligne supérieure de la solution du système. La solution de l’équation d’origine est donc
est la ligne supérieure de la solution du système. La solution de l’équation d’origine est donc
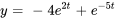
Prenons un exemple
Section 6.6 Exercices
- Résous le système d’équations différentielles avec les valeurs initiales données.
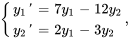
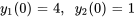
Afficher/Masquer la réponse
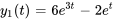
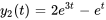
- Résous le système d’équations différentielles
![bb"y"'=[(-17,-30),(4,5)] bb"y" bb"y"'=[(-17,-30),(4,5)] bb"y"](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/16a9cdc00eb185f4eb6edffaad1b2e1f.png)
Afficher/Masquer la réponse
![bb"y"(t)=c_1e^(-5t)[(-5),(2)]+c_2e^(-7t)[(-3),(1)] bb"y"(t)=c_1e^(-5t)[(-5),(2)]+c_2e^(-7t)[(-3),(1)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/c6a6c987b653f4658581558794aad5c5.png)
- Résous le système d’équations différentielles
![bb"y"'=[(1,-12,7),(0,-10,6),(0,-12,8)] bb"y", bb"y"'=[(1,-12,7),(0,-10,6),(0,-12,8)] bb"y",](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/45b18f7335e0614444ea5525da6d09a3.png)
![mathbfy'(0)=[(3),(4),(7)] mathbfy'(0)=[(3),(4),(7)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/cfb92f1fdd46c6ac9b3b7da84d2b00a7.png)
Afficher/Masquer la réponse
![bb"y"(t)=-4e^t[(1),(0),(0)]+3e^(2t)[(2),(1),(2)] +e^(-4t)[(1),(1),(1)] bb"y"(t)=-4e^t[(1),(0),(0)]+3e^(2t)[(2),(1),(2)] +e^(-4t)[(1),(1),(1)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/bfdca9f2ab42722e54281632a9b4726f.png)