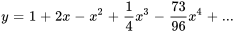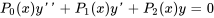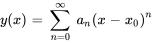5.2 Solutions en séries de puissances d’équations différentielles
Solutions en séries de puissances d’équations différentielles linéaires
Dans les sections précédentes, nous nous sommes principalement intéressés aux équations différentielles linéaires homogènes à coefficients constants. Cependant, de nombreuses applications physiques conduisent à des équations différentielles linéaires homogènes du second ordre plus complexes de la forme
où 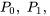 et
et 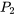 sont des polynômes sans facteur commun. Souvent, les solutions à l’équation de la section 5.2.1 ne peuvent pas être exprimées sous la forme de fonctions familières, ce qui incite à utiliser des solutions en séries. On commence par normaliser l’équation en la divisant par
sont des polynômes sans facteur commun. Souvent, les solutions à l’équation de la section 5.2.1 ne peuvent pas être exprimées sous la forme de fonctions familières, ce qui incite à utiliser des solutions en séries. On commence par normaliser l’équation en la divisant par 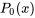 afin que le coefficient de
afin que le coefficient de 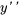 soit égal à 1.
soit égal à 1.
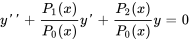
Étant donné la continuité des polynômes, 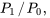 et
et 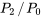 sont continus, sauf éventuellement lorsque
sont continus, sauf éventuellement lorsque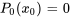 . Un point
. Un point 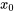 où
où 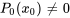 est appelé point ordinaire de l’équation de la section 5.2.1; sinon, c’est un point singulier. Il faut savoir que, aux points ordinaires,
est appelé point ordinaire de l’équation de la section 5.2.1; sinon, c’est un point singulier. Il faut savoir que, aux points ordinaires, 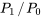 et
et 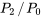 sont analytiques, ce qui autorise la représentation en série de puissances.
sont analytiques, ce qui autorise la représentation en série de puissances.
Théorème. Supposons que 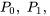 et
et 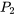 sont des polynômes sans facteur commun et que
sont des polynômes sans facteur commun et que 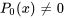 . Si
. Si 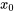 est un point ordinaire de l’équation de la section 5.2.1, de sorte que chaque solution de l’équation peut être représentée par une série de puissances.
est un point ordinaire de l’équation de la section 5.2.1, de sorte que chaque solution de l’équation peut être représentée par une série de puissances.
En outre, le rayon de convergence 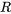 d’une telle solution en série de puissances est au moins aussi grand que la distance entre
d’une telle solution en série de puissances est au moins aussi grand que la distance entre 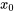 et le point singulier (réel ou complexe) le plus proche de l’équation. Si
et le point singulier (réel ou complexe) le plus proche de l’équation. Si 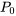 est constant, c’est-à-dire jamais nul, le rayon de convergence sera infini et l’intervalle de convergence sera
est constant, c’est-à-dire jamais nul, le rayon de convergence sera infini et l’intervalle de convergence sera 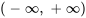 .
.
Pour trouver la solution en série de l’équation de la section 5.2.1, on considère une série de puissances convergeant près d’un point ordinaire 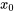 . En supposant que la solution peut être écrite sous forme de série de puissances (section 5.2.2), on remplace
. En supposant que la solution peut être écrite sous forme de série de puissances (section 5.2.2), on remplace 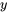 et ses dérivées dans l’équation différentielle donnée et on rassemble les puissances similaires de
et ses dérivées dans l’équation différentielle donnée et on rassemble les puissances similaires de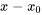 . En fixant le coefficient de chaque puissance à zéro, on peut systématiquement trouver la valeur des coefficients
. En fixant le coefficient de chaque puissance à zéro, on peut systématiquement trouver la valeur des coefficients 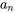 , ce qui donne souvent une relation récursive.
, ce qui donne souvent une relation récursive.
Comment trouver une solution en série à une équation différentielle
1. Déterminer l’équation différentielle et choisir le point 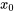 autour duquel développer la série (généralement un point ordinaire).
autour duquel développer la série (généralement un point ordinaire).
2. Supposer une solution en série de puissances (équation de la section 5.2.2) pour 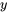 et trouver ses dérivées
et trouver ses dérivées 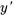 ,
, 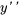 , etc., comme l’exige l’équation différentielle.
, etc., comme l’exige l’équation différentielle.
3. Remplacer la série et ses dérivées dans l’équation différentielle.
4. Organiser les puissances similaires 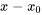 en alignant les termes, de façon à ce que toutes les séries soient exprimées à partir de la même valeur de départ de
en alignant les termes, de façon à ce que toutes les séries soient exprimées à partir de la même valeur de départ de  .
.
5. Regrouper les coefficients des puissances similaires de 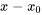 .
.
6. Résoudre les équations en mettant en équation les coefficients de puissances similaires de 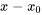 pour trouver des relations entre les
pour trouver des relations entre les 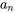 ‘s.
‘s.
7. Utiliser les conditions initiales ou limites données pour trouver des 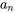 spécifiques. Utiliser la relation récursive pour déterminer tous les coefficients.
spécifiques. Utiliser la relation récursive pour déterminer tous les coefficients.
8. Construire la solution avec les coefficients trouvés et examiner le rayon et l’intervalle de convergence.
Déterminer une solution en série à l’équation différentielle

Afficher/Masquer la solution
1. Étant donné que  , les coefficients sont analytiques en tout point. On suppose que
, les coefficients sont analytiques en tout point. On suppose que 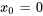 et que la solution peut être écrite sous forme de série de puissances.
et que la solution peut être écrite sous forme de série de puissances.
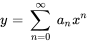
2. Il faut d’abord trouver 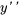 :
:
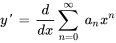
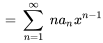
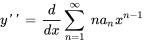
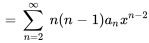
3. Ensuite, on remplace 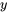 et
et 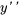 dans l’équation :
dans l’équation :

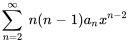
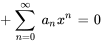
4. L’étape suivante consiste à aligner les termes. Pour ce faire, il faut déplacer les indices de sommation de façon à ce qu’ils commencent à la même valeur. Si 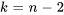 ou
ou 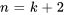 dans la première sommation et
dans la première sommation et 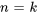 dans la deuxième sommation, on a
dans la deuxième sommation, on a


5. En additionnant les séries, on obtient
![somme_(k=0)^oo\ [(k+2)(k+1) a_(k+2)+a_k] x^(k) =0 somme_(k=0)^oo\ [(k+2)(k+1) a_(k+2)+a_k] x^(k) =0](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/1da7da7308d332963030da00af07ae55.png)
6. D’après la propriété des séries de puissances disparaissant sur un intervalle vue à la section 5.1, on sait que si une série de puissances est nulle  , alors tous ses coefficients doivent être nuls. On en conclut donc que
, alors tous ses coefficients doivent être nuls. On en conclut donc que
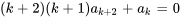
ou
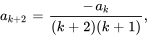
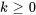
C’est ce que l’on appelle la relation de récurrence pour les valeurs de 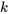 pour lesquelles la relation est vraie.
pour lesquelles la relation est vraie.
7. Ensuite, on écrit quelques termes de la série pour voir si l’on peut déterminer la tendance et, avec un peu de chance, la formule explicite de la série. Quand 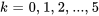 , on a
, on a
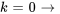 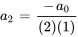 |
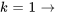 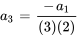 |
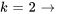 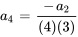 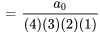 |
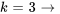 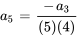  |
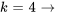 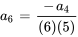 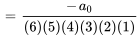 |
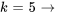 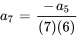 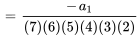 |
On remarque que le terme avec des indices pairs peut être écrit par rapport au terme précédent et même en termes de 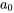 et qu’il en va de même avec les indices impairs en termes de
et qu’il en va de même avec les indices impairs en termes de 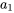 . Par conséquent, en écrivant la relation de récurrence séparément pour les indices (
. Par conséquent, en écrivant la relation de récurrence séparément pour les indices (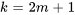 ) impairs et les indices (
) impairs et les indices (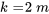 ) pairs, on obtient
) pairs, on obtient
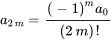
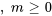
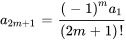
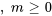
8. La solution générale de l’équation peut donc être écrite sous la forme
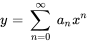
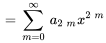
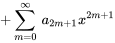
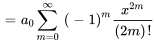
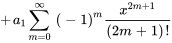
On constate que les séries dans la solution sont les séries de Maclaurin de 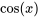 et de
et de 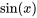 , respectivement.
, respectivement.
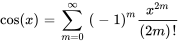 et
et 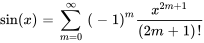
Par conséquent, la solution générale de l’équation peut être exprimée sous la forme
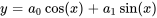
pour des constantes arbitraires 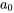 et
et 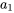 . Cette solution est identique à celle que nous obtiendrions avec les méthodes abordées aux sections précédentes.
. Cette solution est identique à celle que nous obtiendrions avec les méthodes abordées aux sections précédentes.
L’intervalle de convergence pour les séries de cosinus et de sinus est constitué de tous les nombres réels 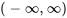 .
.
Pour les deux séries de la solution, le test de ratio indique que, à mesure que  , la limite
, la limite 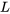 approche de zéro, ce qui signifie que la série converge pour tous les nombres réels. Partant, sans connaissance préalable des séries représentant le sinus et le cosinus, on conclurait que l’intervalle de convergence pour chaque série et donc la solution de séries combinées est un nombre réel entier
approche de zéro, ce qui signifie que la série converge pour tous les nombres réels. Partant, sans connaissance préalable des séries représentant le sinus et le cosinus, on conclurait que l’intervalle de convergence pour chaque série et donc la solution de séries combinées est un nombre réel entier 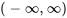 .
.
Prenons un exemple
Dans la pratique, nous essayons de trouver des solutions en série pour des équations à coefficients non constants. En effet, les équations à coefficients constants peuvent être facilement résolues à l’aide de la technique décrite au chapitre 3 pour les équations homogènes à coefficients constants. Prenons un autre exemple pour une équation à coefficients non constants.
Trouver une solution en série à l’équation différentielle

Afficher/Masquer la solution
1. On note que 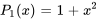 n’a pas de racine, de sorte que chaque point dans cette équation constitue un point ordinaire. On suppose que la solution peut être écrite sous forme de série de puissances.
n’a pas de racine, de sorte que chaque point dans cette équation constitue un point ordinaire. On suppose que la solution peut être écrite sous forme de série de puissances.
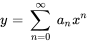
2. Ensuite, on trouve 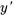 et
et 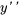 :
:
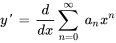
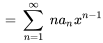
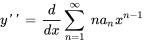
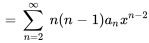
3. On remplace maintenant 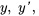 et
et 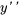 dans l’équation :
dans l’équation :
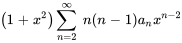
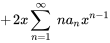
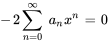
En multipliant les coefficients par la série, on obtient
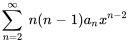
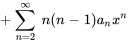
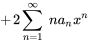
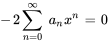
4. On observe que l’exposant de  est le même dans toutes les séries sauf la première. Il suffit donc de décaler l’indice des premières sommations de 2 :
est le même dans toutes les séries sauf la première. Il suffit donc de décaler l’indice des premières sommations de 2 :
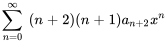
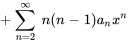
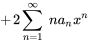
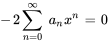
On remarque maintenant que la deuxième série est nulle à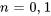 . L’indice peut donc commencer à
. L’indice peut donc commencer à  . Pareillement, la troisième série est nulle à
. Pareillement, la troisième série est nulle à  , de sorte qu’elle peut aussi commencer à
, de sorte qu’elle peut aussi commencer à  . On réécrit donc les indices pour obtenir
. On réécrit donc les indices pour obtenir
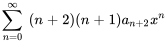
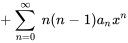
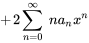
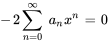
5. En combinant les séries, on obtient
![somme_(n=0)^oo\ [(n+2)(n+1) a_(n+2)+(n(n-1)+2n-2)a_n] x^n=0 somme_(n=0)^oo\ [(n+2)(n+1) a_(n+2)+(n(n-1)+2n-2)a_n] x^n=0](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/1e33a81a0ec721cff0c0719147f7d574.png)
![somme_(n=0)^oo\ [(n+2)(n+1) a_(n+2)+(n^2+n-2)a_n] x^n=0 somme_(n=0)^oo\ [(n+2)(n+1) a_(n+2)+(n^2+n-2)a_n] x^n=0](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/f64159e969f5ec9cafcc8b2df42505d4.png)
6. En définissant un coefficient nul, on obtient
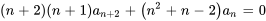
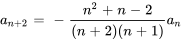
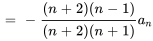
7. La relation récursive peut donc être simplifiée en
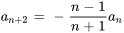
Avec  , on obtient
, on obtient
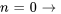 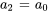 |
 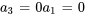 |
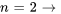 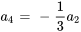 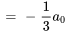 |
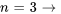 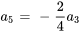  |
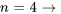 > > 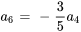  |
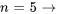 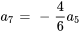  |
On remarque que tous les termes à indices impairs sont nuls sauf 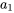 . Par conséquent, en écrivant la relation de récurrence séparément pour les indices (
. Par conséquent, en écrivant la relation de récurrence séparément pour les indices (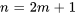 ) impairs et les indices (
) impairs et les indices (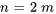 ) pairs, on obtient
) pairs, on obtient

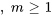
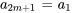
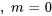
8. La solution générale de l’équation peut donc être écrite sous la forme
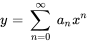
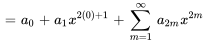
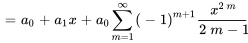
Trouver les six premiers termes dans la solution en série du problème de valeur initiale
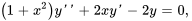
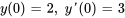
Afficher/Masquer la solution
L’exemple de la section 5.2.2 a donné la solution en série de puissances de cette équation différentielle.
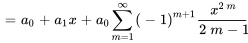
Pour appliquer les conditions initiales, on reconnaît d’abord que 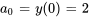 et
et 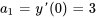 . Ensuite, on remplace
. Ensuite, on remplace 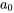 et
et 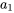 dans la solution générale afin de calculer les autres termes.
dans la solution générale afin de calculer les autres termes.
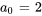
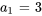
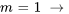
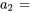
![a_0[(-1)^(1+1)x^(2(1))/(2(1)-1)] a_0[(-1)^(1+1)x^(2(1))/(2(1)-1)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/c3f0acc4c7fb6134827403b64e5949de.png)
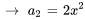
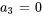
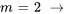
![a_4=a_0[(-1)^(2+1)x^(2(2))/(2(2)-1)] a_4=a_0[(-1)^(2+1)x^(2(2))/(2(2)-1)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/bfc45a5d9c306b6cec9135c47d626d99.png)
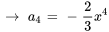
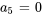
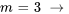
![a_6=a_0[(-1)^(3+1)x^(2(3))/(2(3)-1)] a_6=a_0[(-1)^(3+1)x^(2(3))/(2(3)-1)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/086651c115e9cc96d60c02073f6cda13.png)
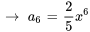

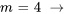
![a_8=a_0[(-1)^(4+1)x^(2(4))/(2(4)-1)] a_8=a_0[(-1)^(4+1)x^(2(4))/(2(4)-1)]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/7b31549a8d2fe7870cf6339200666995.png)
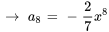
La solution du problème de valeur initiale est donc
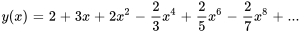 .
.
Prenons un exemple
Section 5.2 Exercices
- Trouve les six premiers termes dans la solution en série du problème de valeur initiale

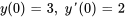
Afficher/Masquer la réponse
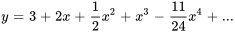
- Trouve les six premiers termes dans la solution en série du problème de valeur initiale
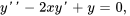
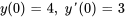
Afficher/Masquer la réponse
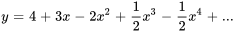
- Trouve les six premiers termes dans la solution en série du problème de valeur initiale
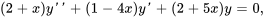
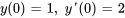
Afficher/Masquer la réponse