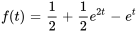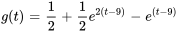4.6 PVI avec fonctions de forçage définies par morceaux
Résolution de problèmes de valeur initiale avec des fonctions de forçage définies par morceaux
Dans la section suivante, nous abordons les problèmes de valeur initiale (PVI) pour des équations différentielles du second ordre à coefficients constants lorsque la fonction de forçage 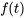 est une fonction continue par morceaux.
est une fonction continue par morceaux.

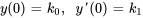
Comment résoudre des PVI avec des fonctions de forçage définies par morceaux au moyen de la méthode de la transformée de Laplace
1. Écrire la fonction de forçage définie par morceaux en termes de fonction en escalier.
2. Déterminer la transformée de Laplace de l’équation différentielle.
3. Résoudre l’équation transformée pour 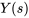 .
.
4. Utiliser les tables de transformées de Laplace et le théorème de translation vus dans les sections précédentes pour déterminer la transformée inverse de Laplace.
5. Au besoin, réécrire 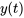 sous forme définie par morceaux.
sous forme définie par morceaux.
Résoudre le problème de valeur initiale donné.
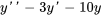
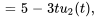
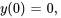
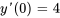
Afficher/Masquer la solution
1. La fonction de forçage 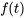 est déjà sous la forme modulée par échelons, avec
est déjà sous la forme modulée par échelons, avec 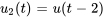 .
.
2. En prenant la transformée de Laplace de l’équation, on a
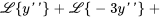
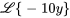
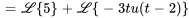
Soit 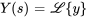 et sachant que
et sachant que 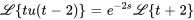 (application de l’équation de la section 4.5.3), on obtient
(application de l’équation de la section 4.5.3), on obtient
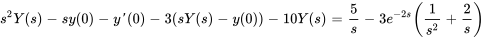
En appliquant les conditions initiales, on obtient
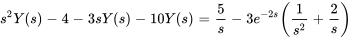
3. La résolution pour 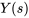 donne
donne
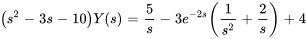
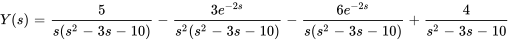
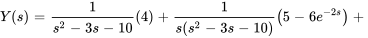
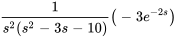
En factorisant les dénominateurs, on obtient
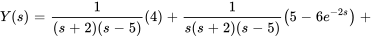

4. Pour trouver 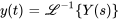 , on note que
, on note que
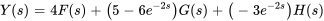
où
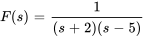
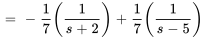
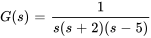
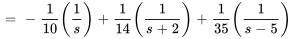
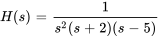
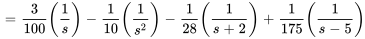
En calculant la transformée inverse de Laplace de 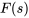 ,
, 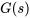 et
et 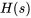 , on obtient
, on obtient
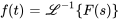
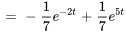
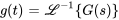
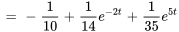
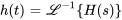
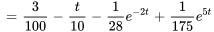
Pour faciliter le processus d’inversion, on réécrit d’abord 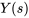 .
.
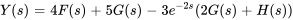
En prenant la transformée inverse et en appliquant le théorème de translation pour les termes avec le terme exponentiel, on obtient
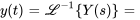
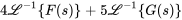
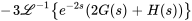
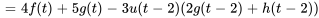
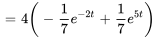
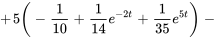
![3u_2(t)[2(-1/10+1/14e^(-2(t-2))+1/35e^(5(t-2)))+(3/100-(t-2)/10-1/28e^(-2(t-2))+1/175e^(5(t-2)))] 3u_2(t)[2(-1/10+1/14e^(-2(t-2))+1/35e^(5(t-2)))+(3/100-(t-2)/10-1/28e^(-2(t-2))+1/175e^(5(t-2)))]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/596f76ddc59a249d749de6abf59be83f.png)
Prenons un exemple
Le courant 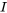 dans un circuit série
dans un circuit série 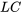 est régi par le problème de valeur initiale suivant. Déterminer le courant en termes de
est régi par le problème de valeur initiale suivant. Déterminer le courant en termes de  .
.
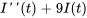
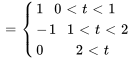
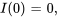
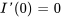
Afficher/Masquer la solution
1. La fonction de forçage 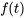 peut être écrite en termes de fonction en escalier sous la forme
peut être écrite en termes de fonction en escalier sous la forme
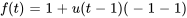
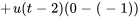
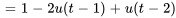
2. En prenant la transformée de Laplace de l’équation, on a
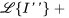
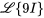
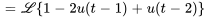
Si 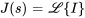 , on obtient
, on obtient
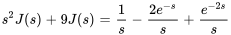
3. La solution pour 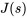 donne
donne
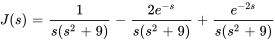
4. Pour trouver 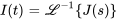 , on note que
, on note que
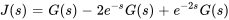
où
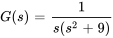
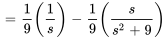
En calculant le transformée inverse de Laplace de 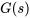 , on obtient
, on obtient
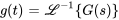
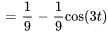
En appliquant le théorème de translation, on obtient
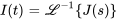
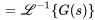
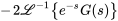
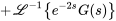
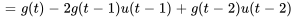
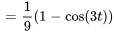
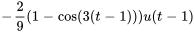
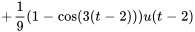
5. Ce résultat peut être écrit sous la forme de la fonction définie par morceaux
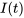
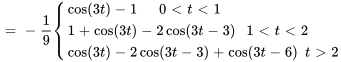
La figure ci-dessous représente le graphique du courant 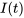 .
.
Prenons un exemple
Section 4.6 Exercices
- Résous le problème de valeur initiale suivant. Ne donne que la solution de
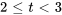 .
.
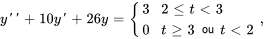
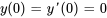
Afficher/Masquer la réponse
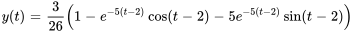
- La solution du PVI
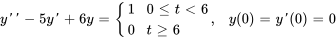
présente la forme
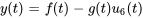 . Trouve les fonctions
. Trouve les fonctions 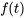 et
et 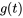 .
.Afficher/Masquer la réponse
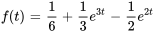
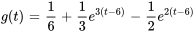
- La solution du PVI
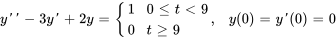
présente la forme
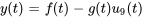 . Trouve les fonctions
. Trouve les fonctions 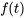 et
et 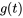 .
.Afficher/Masquer la réponse