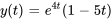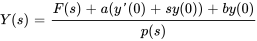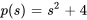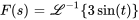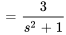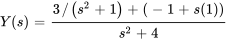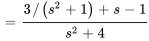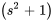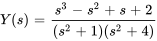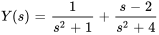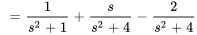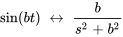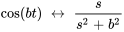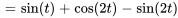4.4 Résolution de problèmes de valeur initiale
Maintenant que nous avons vu la transformée de Laplace, son inverse et ses propriétés, nous sommes en mesure de résoudre des problèmes de valeur initiale (PVI) pour des équations différentielles linéaires. Nous nous concentrerons sur les équations différentielles linéaires du second ordre à coefficients constants.
Méthode de transformée de Laplace pour des PVI
Approche générale :
1. Appliquer la transformée de Laplace pour chaque terme de l’équation différentielle. Utiliser les propriétés de la transformée de Laplace indiquées dans les tables 4.1 et 4.2 afin d’obtenir une équation en termes de 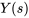 . Les transformées de Laplace des dérivées sont
. Les transformées de Laplace des dérivées sont
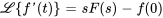
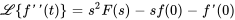
2. Les transformées des dérivées impliquent des conditions initiales à 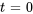 . Appliquer les conditions initiales.
. Appliquer les conditions initiales.
3. Simplifier l’équation transformée pour isoler 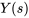 .
.
4. Au besoin, utiliser la décomposition en fractions partielles pour décomposer 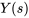 en composants plus simples.
en composants plus simples.
5. Déterminer la transformée inverse de Laplace au moyen des tables et de la propriété de linéarité pour trouver 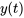 .
.
Approche abrégée :
1. Trouver la caractéristique polynomiale de l’équation différentielle 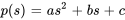 .
.
2. Remplacer 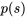 ,
, 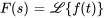 et les conditions initiales dans l’équation
et les conditions initiales dans l’équation
3. Au besoin, utiliser la décomposition en fractions partielles pour décomposer 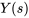 en composants plus simples.
en composants plus simples.
4. Déterminer la transformée inverse de Laplace 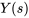 au moyen des tables et de la propriété de linéarité pour trouver
au moyen des tables et de la propriété de linéarité pour trouver 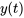 .
.
Résoudre le problème de valeur initiale
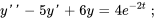
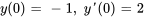
Afficher/Masquer la solution
Approche générale
1. Prendre la transformée de Laplace des deux côtés de l’équation
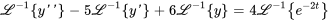
Si 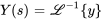 , on obtient
, on obtient
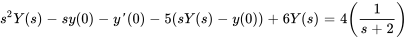
2. Introduire dans les conditions initiales pour obtenir
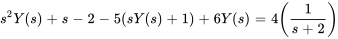
3. Rassembler des termes similaires et isoler 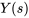 pour obtenir
pour obtenir
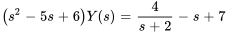
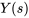
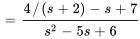
Multiplier le dénominateur et le numérateur par  et factoriser le dénominateur pour obtenir
et factoriser le dénominateur pour obtenir
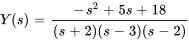
4. Décomposer en fractions partielles pour obtenir
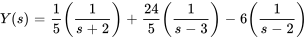
5. À partir de la table 4.1, on voit que
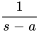
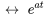
En prenant l’inverse, on obtient la solution de l’équation
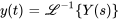
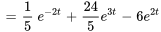
Résoudre le problème de valeur initiale
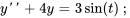
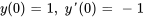
Afficher/Masquer la solution
Approche abrégée :1. Le polynôme caractéristique est
Prenons un exemple
Section 4.4 Exercices
- Résous le PVI en utilisant la transformée inverse de Laplace
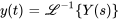
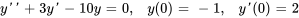
Afficher/Masquer la réponse
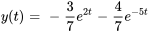
- Résous le PVI en utilisant la transformée inverse de Laplace
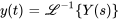
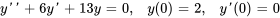
Afficher/Masquer la réponse
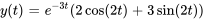
- Résous le PVI en utilisant la transformée inverse de Laplace
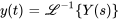
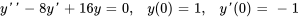
Afficher/Masquer la réponse