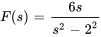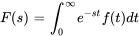4.1 Définitions
A. Introduction
Dans cette section, nous nous intéressons à un opérateur intégral connu sous le nom de transformée de Laplace. Ce puissant outil est employé pour convertir des problèmes de valeur initiale décrits par des équations différentielles dans un domaine (ex. : domaine t) en équations algébriques d’un autre domaine (domaine s). Il s’ensuit un processus de résolution plus efficace, en particulier pour les équations différentielles linéaires à coefficients constants et à termes de forçage discontinus ou impulsifs. Par exemple, considérons un problème de valeur initiale dans le domaine temporel
Domaine-t :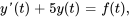 
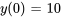
En appliquant la transformée de Laplace, l’équation différentielle est transformée en équation algébrique dans le domaine s :
Domaine-s :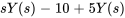 
La représentation algébrique dans le domaine s est souvent plus simple à résoudre, sachant que la solution peut être retransformée dans le domaine t d’origine.
B. Définition
Disons que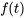 
est une fonction définie sur [0,oo) »>
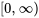et que 
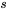est un nombre réel. La transformée de Laplace de 
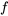est la fonction 
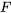définie par l’intégrale
La transformée de Laplace de 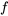est dénotée à la fois par 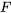et par 
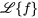. Les fonctions peuvent également être exprimées par une paire transformée 
.
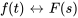L’intégrale impropre dans la définition 4.1.1 est plus précisément définie comme suit :
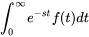
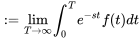
L’intégrale converge, c’est-à-dire qu’elle aboutit à un nombre fini lorsque cette limite existe et est finie.
Trouver la transformée de Laplace de la fonction constante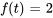 
.
Afficher/Masquer la solution
En remplaçant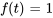 
dans l’intégrale 4.1.1 de la définition de la transformée de Laplace, on obtient
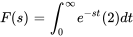
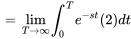
_0^T »>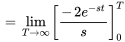
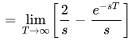
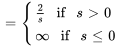
On note que l’intégrale diverge pour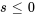 
, de sorte que le domaine de 
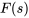est 
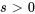. Comme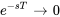 
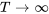pour un 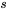fixe, on obtient alors
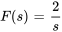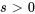for ou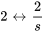 
comme paire transformée
En général, la transformée de Laplace de la fonction constante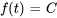 
est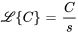 
.
Trouver la transformée de Laplace de la fonction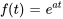 
.
Afficher/Masquer la solution
En remplaçant 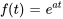dans l’intégrale 4.1.1 de la définition de la transformée de Laplace, on obtient
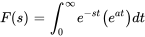
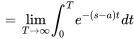
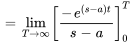
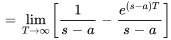
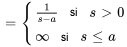
On note que l’intégrale diverge pour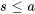 
, de sorte que le domaine de 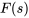est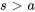 
. Par conséquent,
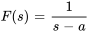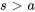for ou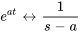 
comme paire transformée
En pratique, bien que la définition de la transformée de Laplace implique une intégrale, elle est rarement calculée directement par intégration en raison de la complexité et de la lenteur du processus. Au lieu de cela, nous utilisons généralement des tables précalculées de transformées de Laplace. Ces tables répertorient les fonctions courantes et leurs transformées correspondantes, ce qui permet une application rapide et précise de la transformée de Laplace pour résoudre des équations différentielles et analyser des systèmes. La table 4.1.1 recense la transformée de Laplace de certaines fonctions courantes. Une table plus complète figure à la section 4.8.
Table 4.1.1 : Table synthétique des transformées de Laplace
| |
 |
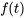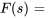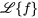Domaine de |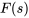
 |
 |
|
 |
 |
|
  |
 |
|
 |
 |
|
 |
 |
|
 |
 |
|
 |
 |
|
 |
 |
|
 |
 |
|
 |
 |
 |
 |
 |
|
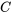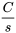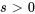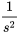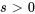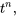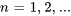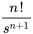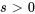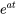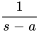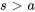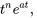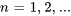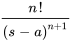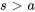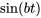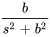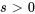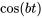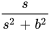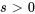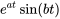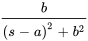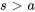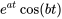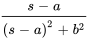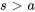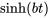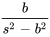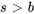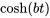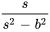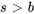Utiliser la table des transformées de Laplace pour déterminer la transformée de Laplace de la fonction suivante :
a)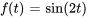 
b)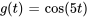 
Afficher/Masquer la solution
a) À partir de la table
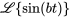
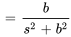pour
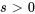
Sachant que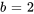 
, la transformée est
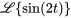
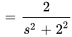pour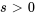 
b) À partir de la table
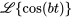
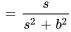pour
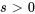
Sachant que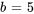 
, la transformée est
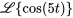
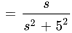pour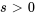
Prenons un exemple
Section 4.1 Exercices
- Trouve la transformée de Laplace, 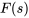, de la fonction
.
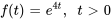Afficher/Masquer la réponse
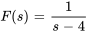
- Trouve la transformée de Laplace, 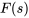, de la fonction
.
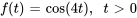Afficher/Masquer la réponse
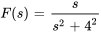
- Trouve la transformée de Laplace de la fonction
.
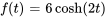
Afficher/Masquer la réponse
