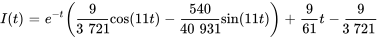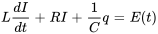3.9 Application : circuits électriques RLC
Dans cette section 2.5F, nous avons exploré les équations différentielles du premier ordre pour des circuits électriques constitués d’une source de tension dotée soit d’une résistance et d’un inducteur (RL), soit d’une résistance et d’un condensateur (RC). Maintenant que nous savons résoudre les équations différentielles du second ordre, nous sommes prêts à nous lancer dans l’analyse de circuits RLC plus complexes, composés d’une résistance, d’un inducteur et un condensateur.
Jusqu’à présent, nous avons vu que :
- La loi d’Ohm stipule que la baisse de tension
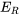 aux bornes d’une résistance est proportionnelle au courant I circulant entre ces bornes, ce qui s’exprime par
aux bornes d’une résistance est proportionnelle au courant I circulant entre ces bornes, ce qui s’exprime par 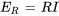 , où
, où 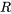 est la résistance.
est la résistance. - La loi de Faraday, complétée par la loi de Lenz, stipule que la baisse de tension
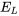 aux bornes d’un inducteur est proportionnelle au taux de variation du courant, ce qui s’exprime par
aux bornes d’un inducteur est proportionnelle au taux de variation du courant, ce qui s’exprime par 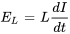 , où
, où 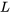 est l’inductance.
est l’inductance. - La baisse de tension
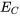 aux bornes d’un condensateur est proportionnelle à la charge électrique
aux bornes d’un condensateur est proportionnelle à la charge électrique 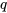 qui y est stockée, représentée par
qui y est stockée, représentée par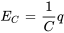 , où
, où 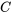 est le condensateur.
est le condensateur.

Figure 3.9.1 Schéma de circuit série RLC
Sur ces bases, considérons que 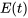 est la tension externe fournie au circuit série RLC représenté à la figure 3.9.1. En appliquant la loi des mailles de Kirchhoff, nous avons
est la tension externe fournie au circuit série RLC représenté à la figure 3.9.1. En appliquant la loi des mailles de Kirchhoff, nous avons
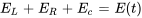
En remplaçant 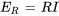 ,
,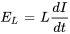 et
et 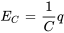 dans cette équation, on obtient
dans cette équation, on obtient
En différenciant cette équation en fonction du temps et en remplaçant 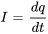 , on la transforme en équation différentielle du seconde ordre.
, on la transforme en équation différentielle du seconde ordre.
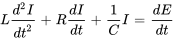 (3.9.2)
(3.9.2)
De même l’équation 3.9.1 peut être exprimée en termes de charge 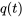 .
.
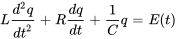 (3.9.3)
(3.9.3)
Étant donné 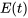 et une condition initiale, telle qu’un courant initial
et une condition initiale, telle qu’un courant initial 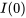 et une charge initiale
et une charge initiale 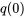 , on peut résoudre l’équation pour
, on peut résoudre l’équation pour 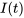 à l’aide des techniques abordées aux sections précédentes, par exemple la méthode des coefficients indéterminés. Une fois que
à l’aide des techniques abordées aux sections précédentes, par exemple la méthode des coefficients indéterminés. Une fois que 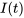 est déterminé, la tension aux bornes des différents composants du circuit peut être calculée.
est déterminé, la tension aux bornes des différents composants du circuit peut être calculée.
Prenons un circuit série RLC avec une résistance de 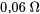 et un inducteur de
et un inducteur de 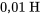 , ainsi qu’un condensateur de
, ainsi qu’un condensateur de 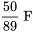 alimenté par une source de tension
alimenté par une source de tension 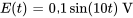 . Au départ, le courant et la charge sur le condensateur sont nuls. Déterminer le courant dans le circuit en fonction du temps.
. Au départ, le courant et la charge sur le condensateur sont nuls. Déterminer le courant dans le circuit en fonction du temps.
Afficher/Masquer la solution
Informations données :
- Résistance :
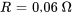
- Inducteur :
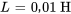
- Condensateur :
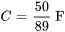
- Source de tension :
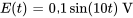
- Courant initial du condensateur :
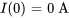
- Charge initiale du condensateur :
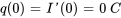
L’équation différentielle pour un circuit série RLC est donnée par l’équation 3.9.1.
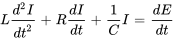
Le problème de valeur initiale est donc
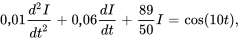
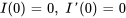
En multipliant l’équation par 100, on obtient
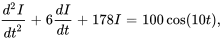
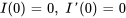
Étant donné que l’équation caractéristique a des racines complexes conjuguées 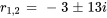 , la solution complémentaire est
, la solution complémentaire est
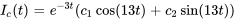
Trouver la solution particulière :
Pour trouver la solution particulière, il faut utiliser la méthode des coefficients indéterminés. Compte tenu de la fonction cosinus de forçage, on suppose que la forme de la solution particulière est
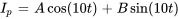
Les dérivées sont
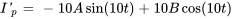
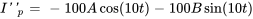
En remplaçant 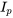 et ses dérivées dans l’équation différentielle, on obtient
et ses dérivées dans l’équation différentielle, on obtient
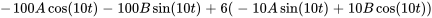
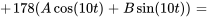
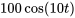
En simplifiant, cela donne
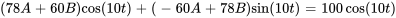
En faisant correspondre les coefficients des termes sinus et cosinus et en résolvant le système de deux équations dans les inconnues 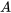 et
et 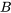 , on obtient
, on obtient
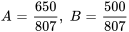
La solution particulière est donc
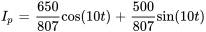
En combinant les solutions particulière et complémentaire, on obtient la solution générale
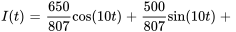
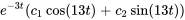
Appliquer les conditions initiales :
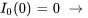
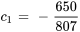
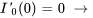
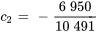
L’équation du déplacement de l’objet est donc
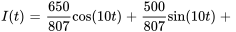
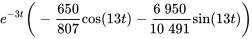
Comme dans les scénarios de vibrations mécaniques forcées, le courant dans un circuit RLC est composé de deux parties distinctes : le courant transitoire, représenté par la solution complémentaire qui diminue à zéro à mesure que le temps progresse vers l’infini, et le courant en régime permanent, décrit par la solution particulière, qui est sinusoïdal et persiste dans le temps.
Prenons un exemple
Section 3.9 Exercices
- Considérons un circuit RLC équipé d’une résistance de
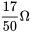 , d’un inducteur de
, d’un inducteur de 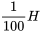 et d’un condensateur de
et d’un condensateur de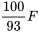 alimenté par la tension
alimenté par la tension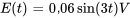 . a) Rédige l’équation différentielle associée à ce circuit en termes de courant
. a) Rédige l’équation différentielle associée à ce circuit en termes de courant 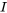 . b) Si la charge initiale et le courant initial du condensateur sont tous les deux nuls, trouve le courant
. b) Si la charge initiale et le courant initial du condensateur sont tous les deux nuls, trouve le courant 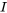 et les tensions aux bornes de la résistance
et les tensions aux bornes de la résistance 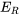 en termes de temps
en termes de temps  .
.
Afficher/Masquer la réponse
a)
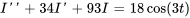
b)
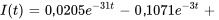
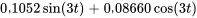
c)
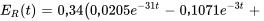
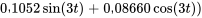
- Considérons un circuit RLC équipé d’une résistance de
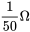 , d’un inducteur de
, d’un inducteur de 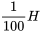 et d’un condensateur de
et d’un condensateur de 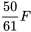 alimenté par la tension
alimenté par la tension 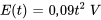 . a) Rédige l’équation différentielle associée à ce circuit en termes de courant
. a) Rédige l’équation différentielle associée à ce circuit en termes de courant 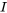 . b) Si la charge initiale et le courant initial du condensateur sont tous deux nuls, trouve le courant
. b) Si la charge initiale et le courant initial du condensateur sont tous deux nuls, trouve le courant 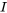 .
.
Afficher/Masquer la réponse
a)
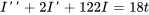
b)