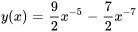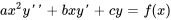3.7 Équation de Cauchy-Euler
L’équation de Cauchy-Euler, également connue sous le nom d’équation d’Euler, est un type d’équation différentielle linéaire du second ordre à coefficients variables qui apparaît dans de nombreuses applications en physique et en ingénierie. Ces équations sont particulièrement remarquables parce que leurs coefficients variables sont des puissances de la variable indépendante.
Les équations de Cauchy-Euler du second ordre présentent généralement la forme suivante :
Ici,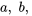 
et 
sont des constantes et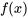 
est une fonction de la variable indépendante. L’équation est homogène si 
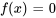et non homogène dans le cas contraire. Par exemple, 
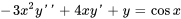est une équation de Cauchy-Euler.
Méthode de résolution d’une équation de Cauchy-Euler homogène
Pour résoudre une équation de Cauchy-Euler homogène 3.7.1,
1. Remplacer et transformer : Soit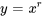 
et forme l’équation caractéristique (auxiliaire). Ainsi, 
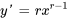et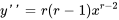 
. En remplaçant cela dans l’équation 3.7.1, on obtient
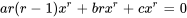
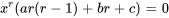
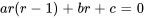
ce qui donne l’équation caractéristique.
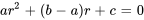
2. Résoudre l’équation caractéristique : Comme pour les équations à coefficients constants, il faut résoudre l’équation quadratique pour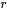 
et, selon la nature des racines, la solution aura différentes formes.
Cas n° 1 : deux racines réelles distinctes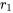 
et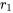
La solution générale sera la combinaison linéaire de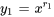 
et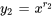 
:
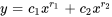
Cas n° 2 : racine répétée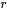
La solution générale sera la combinaison linéaire de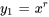 
et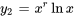 
:
Cas n° 3 : racines complexes conjuguées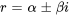 
La solution générale sera la combinaison linéaire de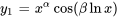 
et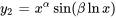 
:
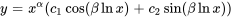
Résoudre le problème de valeur initiale
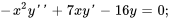
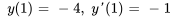
Afficher/Masquer la solution
L’équation est une équation de Cauchy-Euler.
1. Il faut d’abord trouver son polynôme caractéristique donné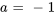 
, 
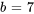et 
:
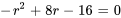
L’équation a une racine répétée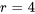 
, qui relève du cas n° 2.
2. La solution générale de l’équation est donc
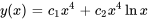
3. Utiliser les valeurs initiales pour trouver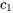 
et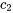 
:
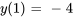
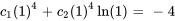
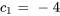
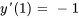
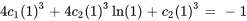
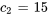
La solution du PVI est donc
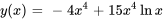
Prenons un exemple
Pour une équation de Cauchy-Euler non homogène, la méthode de variation des paramètres ou des coefficients indéterminés (le cas échéant) est utilisée.
Section 3.7 Exercices
- Trouve la solution générale de l’équation suivante.
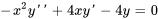
Afficher/Masquer la réponse
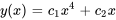
- Résous le problème de valeur initiale
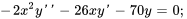
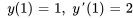
Afficher/Masquer la réponse
