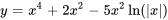3.6 Méthode de réduction d’ordre
La méthode de réduction d’ordre est une technique permettant de trouver une deuxième solution à une équation différentielle linéaire du second ordre lorsqu’une solution est déjà connue. Elle est utile aussi bien pour les équations homogènes que pour les solutions non homogènes.
En général, pour appliquer la méthode de réduction d’ordre pour l’équation non homogène
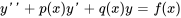
on suppose que la deuxième solution 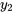 prend la forme
prend la forme 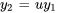 , où
, où 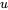 est une fonction de la variable indépendante. En remplaçant
est une fonction de la variable indépendante. En remplaçant 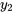 et ses dérivées dans l’équation et en simplifiant, on obtient une équation du premier ordre en termes de
et ses dérivées dans l’équation et en simplifiant, on obtient une équation du premier ordre en termes de 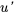 :
:
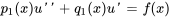
Il est alors possible de résoudre cette équation différentielle du premier ordre à l’aide de techniques standard, de l’intégrer pour trouver 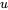 , puis de déterminer
, puis de déterminer 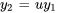 .
.
Méthode de réduction d’ordre pour des équations homogènes
En partant d’une équation homogène avec une solution connue 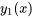 , trouver une deuxième solution linéairement indépendante
, trouver une deuxième solution linéairement indépendante 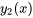 en procédant comme suit :
en procédant comme suit :
1. Standardiser l’équation : diviser l’équation par le coefficient de 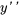 pour que le coefficient soit égal à un. L’équation doit présenter le format suivant :
pour que le coefficient soit égal à un. L’équation doit présenter le format suivant :
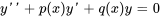
2. Déterminer 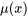 : identifier la fonction
: identifier la fonction 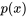 , le coefficient de
, le coefficient de 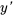 et évaluer l’intégrale :
et évaluer l’intégrale :
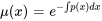
3. Trouver la deuxième solution 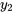 : évaluer l’intégrale suivante pour trouver la deuxième solution : Pour plus de simplicité, disons que la constante d’intégration est nulle.
: évaluer l’intégrale suivante pour trouver la deuxième solution : Pour plus de simplicité, disons que la constante d’intégration est nulle.
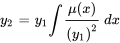
4. Formuler la solution générale : la solution générale est la combinaison linéaire des deux solutions :
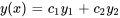
Il convient de noter que la constante 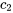 peut absorber n’importe quel coefficient numérique de
peut absorber n’importe quel coefficient numérique de 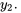
Sachant que 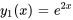 est une solution à l’équation donnée, utilise la méthode de réduction d’ordre pour trouver une deuxième solution.
est une solution à l’équation donnée, utilise la méthode de réduction d’ordre pour trouver une deuxième solution.
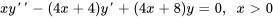
Afficher/Masquer la solution
1. Tout d’abord, standardiser l’équation en la divisant par le coefficient de 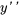 :
:
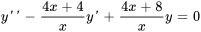
2. Identifier 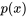 , le coefficient de la fonction de
, le coefficient de la fonction de 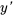 , puis trouver
, puis trouver 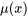 .
.
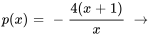
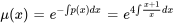
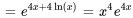
3. La deuxième solution est donnée par
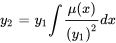
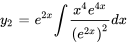
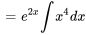
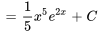
Comme nous recherchons la solution 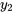 la plus simple, nous définissons une constante d’intégration de zéro. Comme n’importe quel multiple scalaire de
la plus simple, nous définissons une constante d’intégration de zéro. Comme n’importe quel multiple scalaire de 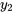 est aussi une solution, on peut choisir
est aussi une solution, on peut choisir 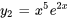 comme étant la deuxième solution la plus simple.
comme étant la deuxième solution la plus simple.
Prenons un exemple
Bien que principalement détaillés pour les équations homogènes, les principes de cette méthode s’appliquent aux situations non homogènes en résolvant d’abord l’équation homogène associée et en trouvant ensuite une solution particulière au moyen des méthodes standard expliquées pour les équations non homogènes.
Sachant que 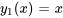 est une solution à l’équation complémentaire, résous le problème de valeur initiale suivant.
est une solution à l’équation complémentaire, résous le problème de valeur initiale suivant.
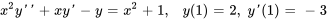
Afficher/Masquer la solution
a. Trouver la deuxième solution de l’équation complémentaire :
Il faut suivre les étapes de la méthode de réduction d’ordre pour trouver la deuxième solution linéairement indépendante à l’équation complémentaire.
1a. Tout d’abord, standardiser l’équation en la divisant par le coefficient de 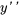 :
:
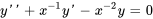
2a. Identifier 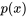 , le coefficient de la fonction de
, le coefficient de la fonction de 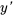 , puis trouver
, puis trouver 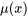 .
.
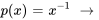
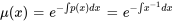
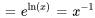
3a. La deuxième solution est donnée par
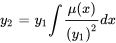
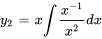
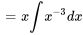
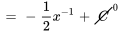
4a. La solution générale de l’équation complémentaire est
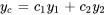
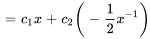
La constante 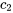 peut absorber n’importe quel coefficient numérique de
peut absorber n’importe quel coefficient numérique de 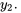 Ainsi,
Ainsi, 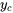 peut être simplifié en
peut être simplifié en
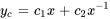
b. Trouver une solution particulière à l’équation non homogène :
Il faut utiliser la méthode de variation des paramètres pour trouver la solution particulière 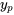 .
.
1b. Standardiser l’équation différentielle d’origine.
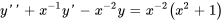
2b. Les solutions de l’équation homogène sont maintenant connues : 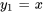 et
et 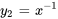 .
.
Le wronskien de l’ensemble fondamental est
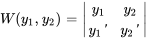
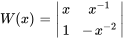
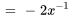
3b. Remplacer ensuite 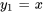 ,
, 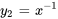 ,
, 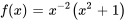 et
et 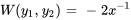 dans des formules pour
dans des formules pour 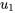 et
et 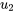 afin de les déterminer.
afin de les déterminer.
Trouver 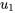 :
:
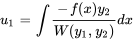
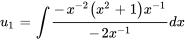
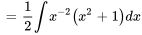
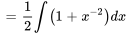
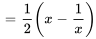
Trouver 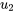 :
:
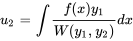
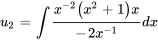
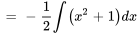
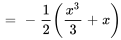
4b. Remplacer 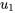 et
et 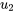 par
par 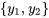 dans l’expression de
dans l’expression de 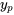 de façon à obtenir une solution particulière :
de façon à obtenir une solution particulière :
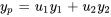
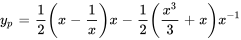
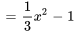
c. Trouver la solution générale
La solution générale de l’équation non homogène est la somme de la solution particulière et de la solution complémentaire.
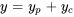
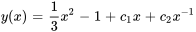
d. Appliquer les conditions initiales
Appliquer la condition initiale à  :
:
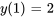
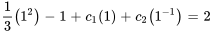
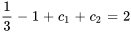
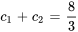
Appliquer la condition initiale à 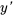 :
:
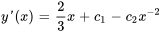
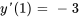
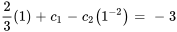
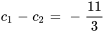
Pour déterminer 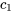 et
et 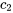 , il faut résoudre le système suivant de deux équations et deux inconnues :
, il faut résoudre le système suivant de deux équations et deux inconnues :
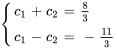
La résolution du système donne
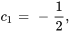
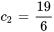
La solution du problème de valeur initiale est donc
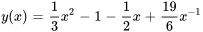
Prenons un exemple
Section 3.6 Exercices
- Sachant que
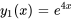 est une solution à l’équation donnée, utilise la méthode de réduction d’ordre pour trouver une deuxième solution.
est une solution à l’équation donnée, utilise la méthode de réduction d’ordre pour trouver une deuxième solution.
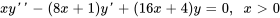
Afficher/Masquer la réponse
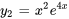
- Trouver la solution générale de l’équation suivante, sachant que
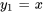 satisfait l’équation complémentaire.
satisfait l’équation complémentaire.
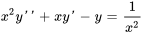
Afficher/Masquer la réponse
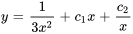
- Résous le problème de valeur initiale, sachant que
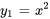 satisfait l’équation complémentaire.
satisfait l’équation complémentaire.
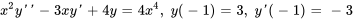
Afficher/Masquer la réponse