3.5 Méthode de variation des paramètres
A. Introduction
La méthode de variation des paramètres est une autre technique permettant de trouver des solutions particulières à des équations différentielles linéaires non homogènes. Elle est particulièrement utile pour les équations à coefficients constants et variables et s’applique lorsque la fonction de forçage,  , rend la méthode des coefficients indéterminés impraticable. Cette technique s’applique également aux équations d’ordre supérieur.
, rend la méthode des coefficients indéterminés impraticable. Cette technique s’applique également aux équations d’ordre supérieur.
Contrairement à la méthode des coefficients indéterminés, où la solution complémentaire permet de deviner la forme de la solution particulière, la variation des paramètres a besoin de la solution complémentaire pour déterminer la solution particulière.
B. Variation des paramètres : équations à coefficients constants
Nous nous concentrons d’abord sur l’application de la méthode de variation des paramètres aux équations non homogènes à coefficients constants. Considérons l’équation linéaire non homogène du second ordre
Soit  un ensemble fondamental de solutions à l’équation complémentaire (homogène) associée. La solution générale de l’équation complémentaire est
un ensemble fondamental de solutions à l’équation complémentaire (homogène) associée. La solution générale de l’équation complémentaire est 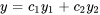 . Pour trouver une solution particulière,
. Pour trouver une solution particulière,  , grâce à la méthode de variation des paramètres, on remplace les constantes
, grâce à la méthode de variation des paramètres, on remplace les constantes  et
et  par les fonctions
par les fonctions  et
et  , respectivement, soit
, respectivement, soit
Le but est de remplacer  et ses dérivées dans l’équation 3.5.1 afin de déterminer des fonctions
et ses dérivées dans l’équation 3.5.1 afin de déterminer des fonctions  et
et  . La dérivée première de
. La dérivée première de  est
est

Comme nous avons plus de paramètres que d’équations, on décide que 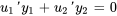 (i) pour simplifier les calculs. Par conséquent,
(i) pour simplifier les calculs. Par conséquent,  est simplifié comme suit :
est simplifié comme suit :
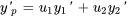
Il faut ensuite trouver 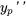 .
.
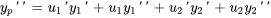
Après avoir remplacé  et ses dérivées dans l’équation 3.5.1 et rassemblé les termes, on obtient
et ses dérivées dans l’équation 3.5.1 et rassemblé les termes, on obtient
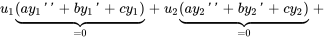
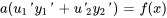
Les expressions multipliées par  et
et  sont nulles, puisque
sont nulles, puisque  et
et  sont des solutions de l’équation complémentaire, d’où
sont des solutions de l’équation complémentaire, d’où
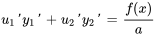 (ii).
(ii).
En combinant (i) et (ii), on obtient un système d’équations
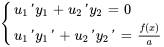
En résolvant le système pour 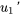 et
et 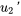 , puis en les intégrant, on obtient les solutions pour
, puis en les intégrant, on obtient les solutions pour  et
et  .
.
 et
et 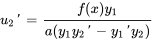
Notez que le terme entre parenthèses est le dénominateur dans le wronskien (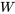 ). Par conséquent,
). Par conséquent, 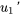 et
et 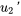 peuvent également s’écrire sous la forme
peuvent également s’écrire sous la forme
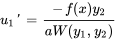 et
et 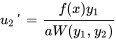
Méthode de variation des paramètres pour des équations à coefficients constants
Pour trouver une solution particulière à l’équation 3.5.1,
1. Trouver une solution à l’équation homogène : déterminer un ensemble fondamental de solutions  à l’équation homogène correspondante et trouver le wronskien des solutions.
à l’équation homogène correspondante et trouver le wronskien des solutions.
2. Déterminer  et
et  : calculer
: calculer 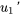 et
et 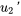 en utilisant le système dérivé de la variation des paramètres. Les intégrer ensuite pour trouver
en utilisant le système dérivé de la variation des paramètres. Les intégrer ensuite pour trouver  et
et  , en prenant une constante d’intégration de zéro :
, en prenant une constante d’intégration de zéro :
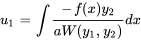 et
et 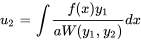
3. Élaborer la solution particulière : combiner  ,
,  ,
,  , et
, et  pour former la solution particulière :
pour former la solution particulière :
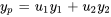
Trouver une solution particulière à
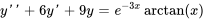
Afficher/Masquer la solution
Pour trouver une solution particulière avec la méthode de variation des paramètres, il faut d’abord trouver une solution à l’équation homogène associée.
1. La caractéristique polynomiale de l’équation complémentaire 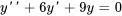 est
est


La solution est donc une racine répétée 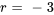 . Partant,
. Partant, 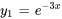 et
et 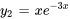 forment un ensemble fondamental de solutions.
forment un ensemble fondamental de solutions.
Le wronskien de l’ensemble fondamental est
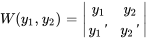
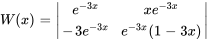

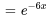
2. Ensuite, il faut remplacer 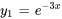 ,
, 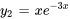 ,
, 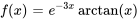 et
et  dans des formules pour
dans des formules pour  et
et  afin de les déterminer.
afin de les déterminer.
Trouver  :
:
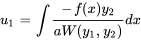

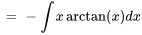
Cette intégrale peut être évaluée au moyen de la technique d’intégration par parties.
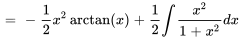
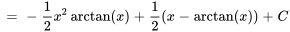
Trouver  :
:
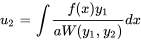
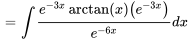
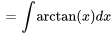
Cette intégrale peut être évaluée au moyen de la technique d’intégration par parties.
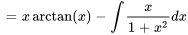

Comme il ne nous faut qu’une solution particulière, nous définissions une constante nulle pour les intégrations dans  et
et  par souci de simplicité.
par souci de simplicité.
3. Il faut maintenant remplacer  et
et  par
par  dans l’expression de
dans l’expression de  pour obtenir une solution particulière :
pour obtenir une solution particulière :
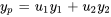
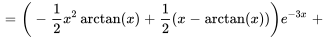
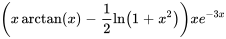

Prenons un exemple
Trouver (a) une solution particulière, puis (b) une solution générale à
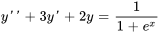
Afficher/Masquer la solution
a) Pour trouver une solution générale, il faut d’abord trouver une solution particulière. Pour trouver une solution particulière avec la méthode de variation des paramètres, il faut d’abord trouver un ensemble fondamental de solutions à l’équation homogène associée :
1. La caractéristique polynomiale de l’équation complémentaire 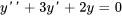 est
est
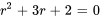
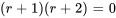
Les solutions sont donc  et
et 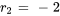 et
et 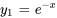 et
et 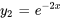 constituent un ensemble fondamental de solutions.
constituent un ensemble fondamental de solutions.
2. Il faut ensuite trouver  et
et  en remplaçant
en remplaçant 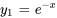 ,
, 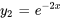 ,
, 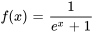 et
et 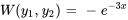 dans
dans
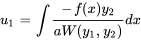
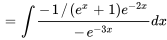

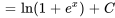
et
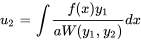

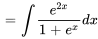
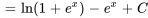
Comme nous n’avons besoin que d’une seule solution particulière, nous définissons les deux constantes sur zéro à des fins de simplicité.
3. Il faut maintenant remplacer  et
et  par
par  dans l’expression de
dans l’expression de  pour obtenir une solution particulière :
pour obtenir une solution particulière :
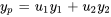
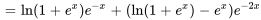
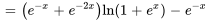
b) Pour trouver une solution générale, il faut ajouter la solution générale à l’équation homogène et à une solution particulière :
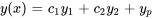
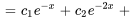
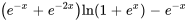
On remarque que les termes 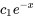 et
et 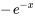 sont analogues et peuvent être combinés en
sont analogues et peuvent être combinés en 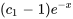 . Puisque
. Puisque 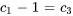 , on obtient
, on obtient
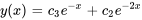
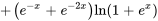
Prenons un exemple
Prenons un exemple
C. Variation des paramètres : équations à coefficients variables
Maintenant que nous savons résoudre des équations différentielles homogènes et non homogènes du second ordre à coefficients constants, passons aux équations dont les coefficients sont des fonctions de la variable indépendante. La méthode de variation des paramètres convient tout à fait à ces équations.
Considérations relatives aux équations à coefficients variables
Pour une équation différentielle de la forme
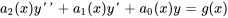
des solutions sont attendues sur un intervalle ouvert où les quatre fonctions directrices, 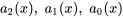 et
et 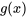 , sont continues et où
, sont continues et où  n’est pas nul. En standardisant l’équation en la divisant par
n’est pas nul. En standardisant l’équation en la divisant par  , on obtient
, on obtient
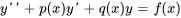
Théorème d’existence et d’unicité des solutions : si  ,
, 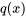 et
et  sont continus sur un intervalle
sont continus sur un intervalle  contenant un point
contenant un point 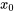 , pour n’importe quelles valeurs initiales
, pour n’importe quelles valeurs initiales 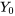 et
et 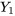 , il existe une solution unique
, il existe une solution unique 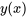 sur le même intervalle que le problème de valeur initiale.
sur le même intervalle que le problème de valeur initiale.
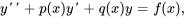

Les étapes méthodologiques pour les équations à coefficients variables sont identiques à celles des équations à coefficients constants, à ceci près que l’équation doit être sous forme standard.
Méthode de variation des paramètres pour des équations à coefficients variables
1. Standardiser l’équation : diviser l’équation par le coefficient de 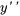 pour que le coefficient soit égal à un. L’équation doit présenter le format suivant :
pour que le coefficient soit égal à un. L’équation doit présenter le format suivant :
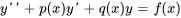
2. Solutions indépendantes linéaires : trouver deux solutions indépendantes linéaires,  à l’équation homogène correspondante. trouver le wronskien des solutions.
à l’équation homogène correspondante. trouver le wronskien des solutions.
3. Déterminer  et
et  : calculer
: calculer 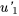 et
et 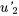 en utilisant le système dérivé de la variation des paramètres. Les intégrer ensuite pour trouver
en utilisant le système dérivé de la variation des paramètres. Les intégrer ensuite pour trouver  et
et  , en prenant une constante d’intégration de zéro :
, en prenant une constante d’intégration de zéro :
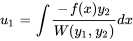 et
et 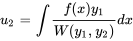
4. Élaborer la solution particulière : combiner  ,
,  ,
,  , et
, et  pour former la solution particulière :
pour former la solution particulière :
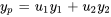
Trouver une solution particulière à l’équation différentielle suivante, sachant que 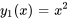 et
et 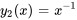 satisfont l’équation homogène correspondante.
satisfont l’équation homogène correspondante.

Afficher/Masquer la solution
1. Diviser d’abord l’équation par le coefficient de 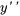 pour lui donner une forme standard.
pour lui donner une forme standard.
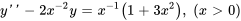
2. Pour trouver une solution particulière avec la méthode de variation des paramètres, il faut un ensemble fondamental de solutions à l’équation homogène associée. Les solutions données  et
et  formeront l’ensemble fondamental si leur wronskien n’est pas nul sur un intervalle ouvert.
formeront l’ensemble fondamental si leur wronskien n’est pas nul sur un intervalle ouvert.
Le wronskien de l’ensemble de solutions est
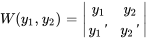
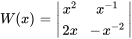

Le wronskien n’est jamais nul. Partant, l’ensemble de solutions est l’ensemble fondamental de solutions.
3. Il faut ensuite remplacer 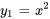 ,
, 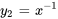 ,
, 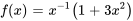 et
et 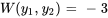 dans des formules pour
dans des formules pour  et
et  afin de les déterminer.
afin de les déterminer.
Trouver  :
:
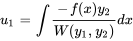
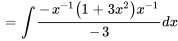
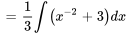
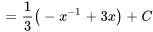
Avec 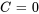 , on obtient
, on obtient
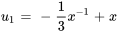
Trouver  :
:
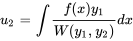
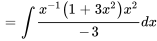
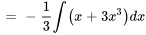
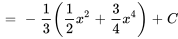
Avec 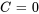 , on obtient
, on obtient
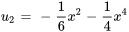
4. Remplacer  et
et  par
par  dans l’expression de
dans l’expression de  de façon à obtenir une solution particulière :
de façon à obtenir une solution particulière :
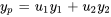
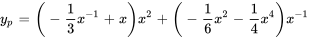

Prenons un exemple
D. Résumé
- Utiliser la méthode des coefficients indéterminés pour des équations à coefficients constants avec des fonctions de forçage reconnaissables
 .
. - Utiliser la méthode de variation des paramètres pour des équations à coefficients constants avec une fonction
 moins typique ou pour des équations à coefficients variables.
moins typique ou pour des équations à coefficients variables. - En général, si un ensemble fondamental de solutions est connu, la variation des paramètres constitue une méthode viable et souvent préférable.
Section 3.5 Exercices
- Trouve une solution particulière à l’équation
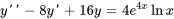
Afficher/Masquer la réponse
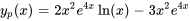
- Trouve la solution particulière à l’équation
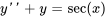
Afficher/Masquer la réponse
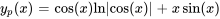
- Trouver une solution particulière à l’équation différentielle suivante, sachant que
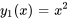 et
et 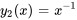 satisfont l’équation homogène correspondante.
satisfont l’équation homogène correspondante.
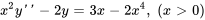
Afficher/Masquer la réponse
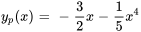
- Trouver une solution particulière à l’équation différentielle suivante, sachant que

