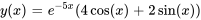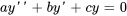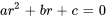3.2 Équations différentielles homogènes à coefficients constants
Considérons en premier lieu l’équation homogène à coefficients constants :
Pour résoudre cette équation, il; faut admettre que la solution doit avoir pour propriété que sa dérivée seconde peut être exprimée comme une combinaison linéaire de la dérivée première et de la fonction elle-même, ce qui suggère que la forme de la solution est 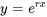 . En remplaçant
. En remplaçant 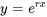 et ses dérivées dans l’équation 3.2.1, on obtient
et ses dérivées dans l’équation 3.2.1, on obtient
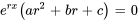
Comme 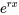 n’est jamais nul pour n’importe quel nombre réel
n’est jamais nul pour n’importe quel nombre réel  , on peut conclure que
, on peut conclure que
L’équation 3.2.2 est appelée l’équation auxiliaire ou l’équation caractéristique (polynôme caractéristique) de l’équation homogène 3.2.1. Pour déterminer la solution générale de l’équation 3.2.1, il faut trouver la valeur de 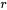 dans l’équation caractéristique.
dans l’équation caractéristique.
Les racines de l’équation caractéristique déterminent la nature de la solution, ce qui conduit à trois cas possibles selon que les racines sont réelles et distinctes, réelles et répétées ou complexes conjuguées.
Solution générale de l’équation différentielle linéaire du second ordre à coefficients constants
Cas n° 1 : deux racines réelles distinctes
Si l’équation caractéristique (équation 3.2.2) a deux racines réelles 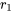 et
et 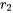 , alors les solutions sont
, alors les solutions sont 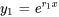 et
et 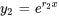 . La solution générale est la combinaison linéaire de ces deux solutions :
. La solution générale est la combinaison linéaire de ces deux solutions :
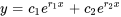
Cas n° 2 : racine répétée
Si l’équation caractéristique a une racine répétée 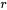 , alors les solutions sont
, alors les solutions sont 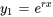 et
et 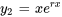 . La solution générale est la combinaison linéaire de ces deux solutions :
. La solution générale est la combinaison linéaire de ces deux solutions :
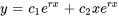
Cas n° 3 : racines complexes conjuguées
Si l’équation caractéristique a des racines complexes conjuguées sous la forme 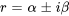 , alors les solutions peuvent être représentées par la formule d’Euler sous la forme
, alors les solutions peuvent être représentées par la formule d’Euler sous la forme 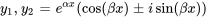 . La solution générale à valeur réelle dérivée de ces solutions complexes est
. La solution générale à valeur réelle dérivée de ces solutions complexes est
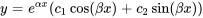
Sous cette forme, 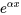 représente la croissance ou la décroissance exponentielle, tandis que la combinaison de cosinus et de sinus représente le comportement oscillatoire dû à la partie complexe des racines.
représente la croissance ou la décroissance exponentielle, tandis que la combinaison de cosinus et de sinus représente le comportement oscillatoire dû à la partie complexe des racines.
Trouver la solution générale de l’équation différentielle
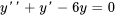
Afficher/Masquer la solution
L’équation auxiliaire est
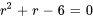
L’équation peut être factorisée en
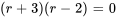
Les racines sont 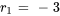 et
et 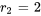 . C’est le cas n° 1 car les racines sont réelles et distinctes. Partant, la solution générale est la combinaison linéaire de
. C’est le cas n° 1 car les racines sont réelles et distinctes. Partant, la solution générale est la combinaison linéaire de 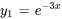 et
et 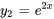 :
:
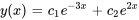
Résoudre le problème de valeur initiale (PVI) suivant.

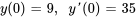
Afficher/Masquer la solution
Trouver la solution générale :
L’équation auxiliaire est
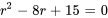
L’équation peut être factorisée en
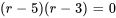
Les racines sont 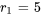 et
et 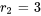 . C’est le cas n° 1 car les racines sont réelles et distinctes. Partant, la solution générale est la combinaison linéaire de
. C’est le cas n° 1 car les racines sont réelles et distinctes. Partant, la solution générale est la combinaison linéaire de 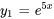 et
et 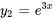 :
:
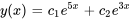
Appliquer les conditions initiales :
Appliquer la condition initiale à  :
:
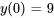
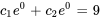
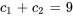
Appliquer la condition initiale à 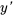 :
:
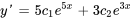
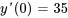
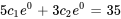
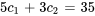
Pour déterminer 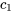 et
et 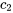 , il faut résoudre le système suivant de deux équations et deux inconnues :
, il faut résoudre le système suivant de deux équations et deux inconnues :
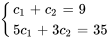
La résolution du système donne
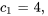
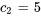
La solution du problème de valeur initiale est donc
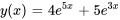
Prenons un exemple
Trouver la solution générale de l’équation différentielle
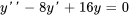
Afficher/Masquer la solution
L’équation auxiliaire est
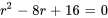
L’équation peut être factorisée en
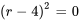
L’équation a une racine répétée 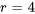 . Il s’agit du cas n° 2, la racine répétée. Partant, la solution générale est la combinaison linéaire de
. Il s’agit du cas n° 2, la racine répétée. Partant, la solution générale est la combinaison linéaire de 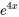 et
et 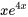 :
:
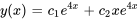
Résoudre le problème de valeur initiale (PVI) suivant.
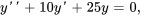
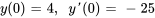
Afficher/Masquer la solution
Trouver la solution générale :
L’équation auxiliaire est
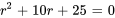
L’équation peut être factorisée en
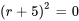
L’équation a une racine répétée 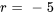 . Il s’agit du cas n° 2, la racine répétée. Partant, la solution générale est la combinaison linéaire de
. Il s’agit du cas n° 2, la racine répétée. Partant, la solution générale est la combinaison linéaire de 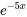 et
et 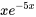 :
:
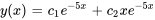
Appliquer les conditions initiales :
Appliquer la condition initiale à  :
:
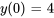
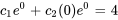
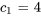
Appliquer la condition initiale à 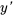 :
:
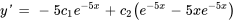
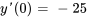
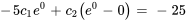
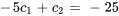
En introduisant cela dans 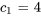 , on obtient
, on obtient 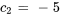 .
.
La solution du problème de valeur initiale est donc
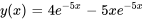
Prenons un exemple
Trouver la solution générale de l’équation différentielle
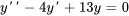
Afficher/Masquer la solution
L’équation auxiliaire est
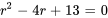
Avec la formule quadratique, on obtient
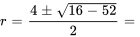
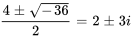
L’équation a des racines complexes conjuguées avec une partie réelle 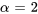 et une partie imaginaire
et une partie imaginaire 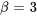 . Il s’agit du cas n° 3, la solution générale est donc
. Il s’agit du cas n° 3, la solution générale est donc
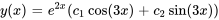
Résoudre le problème de valeur initiale (PVI) suivant.

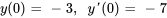
Afficher/Masquer la solution
Trouver la solution générale :
L’équation auxiliaire est
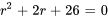
Il est possible de trouver les racines sans faire usage de la formule quadratique vue dans l’exemple précédent, mais par la complétion du carré. Pour varier les plaisirs, nous allons cette fois utiliser la complétion du carré.
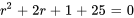
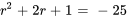
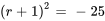
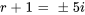
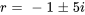
L’équation a des racines complexes conjuguées avec une partie réelle 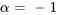 et une partie imaginaire
et une partie imaginaire 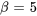 . Il s’agit du cas n° 3, la solution générale est donc
. Il s’agit du cas n° 3, la solution générale est donc
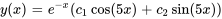
Appliquer les conditions initiales :
Appliquer la condition initiale à  :
:
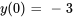
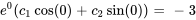
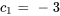
Appliquer la condition initiale à 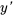 :
:
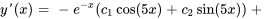
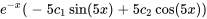
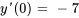
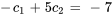
En introduisant cela dans 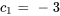 , on obtient
, on obtient 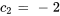 .
.
La solution du problème de valeur initiale est donc
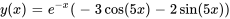
Prenons un exemple
Section 3.2 Exercices
- Résous le problème de valeur initiale donné.
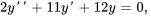
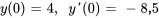
Afficher/Masquer la réponse
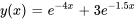
- Résous le problème de valeur initiale donné.
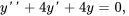
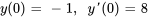
Afficher/Masquer la réponse
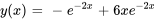
- Résous le problème de valeur initiale donné.
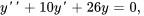
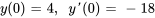
Afficher/Masquer la réponse