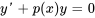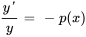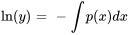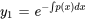2.2 Équations différentielles linéaires du premier ordre
Une équation différentielle du premier ordre est dite linéaire si elle peut être écrite sous la forme
Une équation différentielle du premier ordre qui ne peut pas être exprimée sous cette forme est dite non linéaire. Si 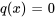 , l’équation est dite homogène. En revanche, si
, l’équation est dite homogène. En revanche, si 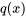 n’est pas égal à zéro, l’équation est non homogène. Les équations homogènes ont toujours la solution triviale
n’est pas égal à zéro, l’équation est non homogène. Les équations homogènes ont toujours la solution triviale 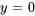 . Les solutions qui ne sont pas nulles sont des solutions non triviales.
. Les solutions qui ne sont pas nulles sont des solutions non triviales.
Certaines équations peuvent ne pas paraître linéaires d’emblée, par exemple  , mais elles peuvent être réarrangées pour prendre une forme linéaire :
, mais elles peuvent être réarrangées pour prendre une forme linéaire :
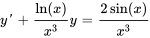 .
.
Théorème : Si  et
et 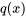 dans l’équation 2.2.1 sont continus sur un intervalle ouvert (a,b), alors il existe une formule unique
dans l’équation 2.2.1 sont continus sur un intervalle ouvert (a,b), alors il existe une formule unique 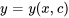 qui est la solution générale à l’équation différentielle.
qui est la solution générale à l’équation différentielle.
Dans cet ouvrage, nous ne mentionnerons pas toujours explicitement l’intervalle lorsque nous chercherons la solution générale d’une équation linéaire du premier ordre spécifique. Par défaut, cela implique que nous recherchons la solution générale sur chaque intervalle ouvert où les fonctions et dans l’équation sont continues.
Pour résoudre l’équation 2.2.1, il faut d’abord supposer que la solution peut être exprimée sous la forme , où est une solution connue à l’équation homogène correspondante (dite équation complémentaire) et  est une fonction inconnue que nous cherchons à déterminer. Cette approche fait partie d’une technique appelée variation des paramètres, qui est particulièrement utile pour trouver des solutions à des équations différentielles non homogènes. Nous étudierons cette technique plus en détail dans le contexte des équations différentielles du second ordre. En substituant la solution devinée à l’équation, on obtient
est une fonction inconnue que nous cherchons à déterminer. Cette approche fait partie d’une technique appelée variation des paramètres, qui est particulièrement utile pour trouver des solutions à des équations différentielles non homogènes. Nous étudierons cette technique plus en détail dans le contexte des équations différentielles du second ordre. En substituant la solution devinée à l’équation, on obtient
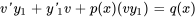
En simplifiant et en réarrangeant, on obtient
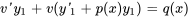
Comme est une solution de l’équation complémentaire, , en simplifiant l’expression à la forme . L’intégration des deux côtés nous permet de déterminer 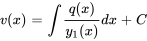 , ce qui donne pour l’équation 2.2.1 la solution
, ce qui donne pour l’équation 2.2.1 la solution
Maintenant que nous comprenons la dérivation de la solution, décrivons le processus de solution dans les étapes suivantes.
Comment résoudre des équations linéaires du premier ordre
1. Écrire l’équation sous sa forme standard.
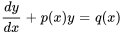
2. Calculer le facteur intégrant en laissant la constante d’intégration à zéro, par souci de commodité.
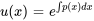
3. Intégrer le côté droit de l’équation et simplifier, dans la mesure du possible. Veiller à traiter correctement la constante de l’intégration.
![y(x)=1/(u(x))[int u(x)q(x)dx+C] y(x)=1/(u(x))[int u(x)q(x)dx+C]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/8046d81727e5e2f09dfbda1f4c74cad3-2.png)
Parfois, la fonction  peut ne pas être directement intégrée. En ce cas, il faut conserver la fonction dans sa forme intégrale, plutôt que d’essayer de trouver une solution explicite.
peut ne pas être directement intégrée. En ce cas, il faut conserver la fonction dans sa forme intégrale, plutôt que d’essayer de trouver une solution explicite.
Trouver la solution générale de
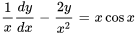 ,
, 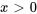
Afficher/Masquer la solution
1. Tout d’abord, il faut multiplier par  pour mettre l’équation sous sa forme standard :
pour mettre l’équation sous sa forme standard :
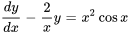
Ainsi, 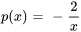 et
et 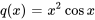
2. Le facteur intégrant est donc
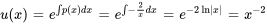
3. En substituant la formule générale, on obtient
![y(x)=1/(u(x))[int u(x)q(x)dx+C] y(x)=1/(u(x))[int u(x)q(x)dx+C]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/8046d81727e5e2f09dfbda1f4c74cad3-2.png)
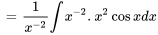
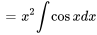
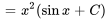
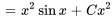
La figure 2.2.1 présente les esquisses des solutions pour différentes valeurs de la constante 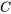 pour l’exemple ci-dessus.
pour l’exemple ci-dessus.
Figure 2.2.1 Graphique de 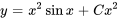 pour différentes valeurs de la constante
pour différentes valeurs de la constante 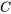
Prenons un exemple
Théorème – Existence et unicité des solutions : Si  et
et 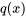 sont continus sur
sont continus sur  , alors
, alors
a) La solution générale à l’équation non homogène est ![y(x)=1/(u(x))[int u(x)q(x)dx+C] y(x)=1/(u(x))[int u(x)q(x)dx+C]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/8046d81727e5e2f09dfbda1f4c74cad3-2.png)
b) Si 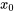 est un point arbitraire dans
est un point arbitraire dans  , alors le problème de valeur initiale a une solution unique sur
, alors le problème de valeur initiale a une solution unique sur 
Résoudre le problème initial
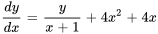 ,
, 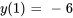
Afficher/Masquer la solution
Trouver la solution générale :
1. Tout d’abord, il faut réarranger l’équation pour la mettre dans sa forme standard :
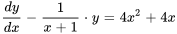
Donc, 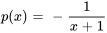 et
et 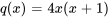 .
.
2. Le facteur intégrant est

3. En substituant la solution à la formule générale, on obtient
![y(x)=1/(u(x))[int u(x)q(x)dx+C] y(x)=1/(u(x))[int u(x)q(x)dx+C]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/8046d81727e5e2f09dfbda1f4c74cad3-2.png)
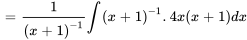
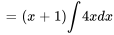
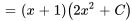
Appliquer la condition initiale pour trouver C :
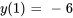
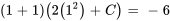
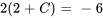
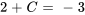
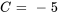
La solution du PVI est donc
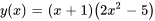
Prenons un exemple
Section 2.2 Exercices
- Trouve le facteur intégrant le plus simple
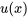 de l’équation
de l’équation 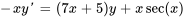 .
.
Afficher/Masquer la réponse
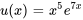
- Trouve la solution générale à l’équation différentielle :
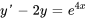
Afficher/Masquer la réponse
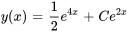
- Trouve la solution générale à l’équation différentielle :
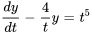
Afficher/Masquer la réponse
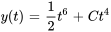
- Résous le problème de valeur initiale :
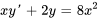 avec la condition initiale
avec la condition initiale 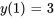
Afficher/Masquer la réponse
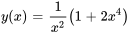
- Résous le problème de valeur initiale :
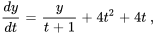

Afficher/Masquer la réponse
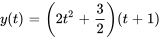

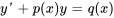
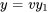
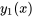

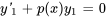
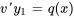
![y(x)=y_1(x)[int(q(x))/(y_1(x))dx+C] y(x)=y_1(x)[int(q(x))/(y_1(x))dx+C]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/fb6cd40e2b2a9110d9c28b65e4d72851-2.png)
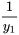
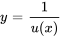
![[int u(x)q(x)dx+C] [int u(x)q(x)dx+C]](https://ecampusontario.pressbooks.pub/app/uploads/sites/4139/2024/03/6ae09153fc3eab62ff6da1e7ea140ae8-2.png)