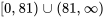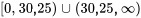2.1 Équations séparables
Les équations séparables, ou équations à variables séparables, sont un type d’équations différentielles du premier ordre qui peuvent être réarrangées de manière à ce que tous les termes impliquant une variable se trouvent d’un côté de l’équation et que tous les termes impliquant l’autre variable se trouvent du côté opposé. Cette caractéristique les rend plus faciles à résoudre que d’autres types d’équations différentielles. Ces équations représentent souvent des relations non linéaires.
La compréhension et l’application des techniques d’intégration sont cruciales pour la résolution des équations séparables. Il est donc recommandé de se familiariser avec les méthodes d’intégration classiques avant de tenter de résoudre ces équations.
Solution d’équation différentielle séparable
Une équation différentielle du premier ordre est dite séparable si elle peut être écrite sous la forme
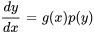
où 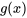 est une fonction de
est une fonction de  uniquement et
uniquement et 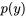 est une fonction de
est une fonction de  uniquement. Le côté droit est un produit de ces deux fonctions, ce qui permet la séparation des variables.
uniquement. Le côté droit est un produit de ces deux fonctions, ce qui permet la séparation des variables.
Par exemple, l’équation 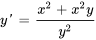 est séparable car elle peut être factorisée et écrite sous la forme
est séparable car elle peut être factorisée et écrite sous la forme 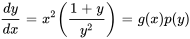 . En revanche, l’équation
. En revanche, l’équation 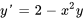 n’est pas séparable car le côté droit ne peut pas être factorisé en un produit des fonctions de
n’est pas séparable car le côté droit ne peut pas être factorisé en un produit des fonctions de  et
et  .
.
Comment résoudre des équations séparables
Pour résoudre l’équation 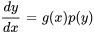 ,
,
1. Séparer les variables : multiplier les deux côtés par 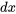 et par
et par 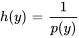

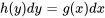
2. Intégrer les deux côtés :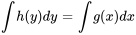

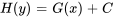 où
où 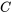 est la constante fusionnée d’intégration.
est la constante fusionnée d’intégration.
3. Trouver la valeur de  : si possible, résoudre l’équation obtenue pour
: si possible, résoudre l’équation obtenue pour  afin d’obtenir la solution explicite. Certaines solutions ne peuvent pas être réarrangées et résolues pour
afin d’obtenir la solution explicite. Certaines solutions ne peuvent pas être réarrangées et résolues pour  , de sorte que la forme implicite obtenue à l’étape 2 peut être la solution finale.
, de sorte que la forme implicite obtenue à l’étape 2 peut être la solution finale.
Regarder la vidéo
Résoudre l’équation non linéaire
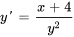 .
.
Afficher/Masquer la solution
1. En multipliant les deux côtés par 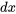 et
et 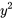 , on obtient
, on obtient
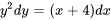
2. En intégrant les deux côtés, on obtient
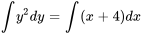
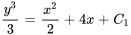
3. En multipliant par 3 et en prenant la racine cubique des deux côtés, on obtient
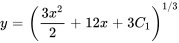
En substituant la constant e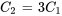 , on obtient la solution explicite
, on obtient la solution explicite
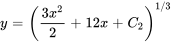
Résoudre l’équation différentielle
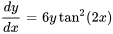 .
.
Afficher/Masquer la solution
Il s’agit d’une équation différentielle séparable car elle peut être exprimée sous la forme 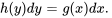
1. En multipliant les deux côtés par 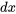 et
et  , on obtient
, on obtient
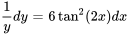
2. En intégrant les deux côtés, on obtient
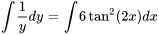
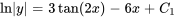
3. Par l’exponentiation des deux côtés, on obtient
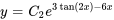 where
where 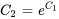
Prenons un exemple
Pour résoudre des équations différentielles non linéaires, il est essentiel de prendre en compte l’intervalle de validité, c’est-à-dire la plage de la variable indépendante, généralement  , où la solution est définie et se comporte comme il se doit. Cet intervalle est essentiel car les solutions d’équations non linéaires peuvent ne pas être valides pour toutes les valeurs
, où la solution est définie et se comporte comme il se doit. Cet intervalle est essentiel car les solutions d’équations non linéaires peuvent ne pas être valides pour toutes les valeurs  en raison de problèmes potentiels tels que la division par zéro, des logarithmes non définis de nombres non positifs et d’autres opérations indéfinies.
en raison de problèmes potentiels tels que la division par zéro, des logarithmes non définis de nombres non positifs et d’autres opérations indéfinies.
En outre, du fait de la nature des équations non linéaires, certaines conditions initiales peuvent conduire à l’absence de solution ou à des solutions multiples, ce qui souligne la nécessité de sélectionner et de vérifier soigneusement la plage de  sur laquelle la solution peut être appliquée. L’intervalle de validité n’est pas toujours immédiatement apparent à partir de l’équation elle-même et dépend souvent à la fois de la forme spécifique de la solution et des conditions initiales.
sur laquelle la solution peut être appliquée. L’intervalle de validité n’est pas toujours immédiatement apparent à partir de l’équation elle-même et dépend souvent à la fois de la forme spécifique de la solution et des conditions initiales.
Résoudre le problème de valeur initiale
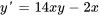 ,
, 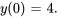
Afficher/Masquer la solution
Trouver la solution générale :
Après avoir factorisé 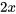 dans le côté droit, l’équation peut être exprimée sous la forme
dans le côté droit, l’équation peut être exprimée sous la forme 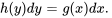
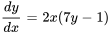
1. En multipliant les deux côtés par 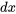 et
et 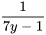 , on obtient
, on obtient
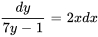
2. En intégrant les deux côtés, on obtient
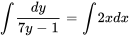
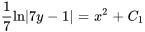
3. En multipliant par 7 et en exponialisant les deux côtés, on obtient
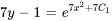
En réarrangeant l’équation et en substituant 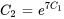 , on obtient la solution explicite
, on obtient la solution explicite
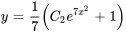
Appliquer la condition initiale :
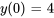
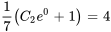
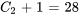
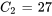
La solution du PVI est donc
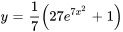
Il n’y a pas de restriction sur le domaine de  , de sorte que la solution est valide sur
, de sorte que la solution est valide sur  .
.
Prenons un exemple
Résoudre le problème de valeur initiale et trouver l’intervalle de validité de la solution.
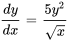 ,
, 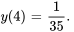
Afficher/Masquer la solution
Trouver la solution générale :
Il s’agit d’une équation différentielle séparable car elle peut être exprimée sous la forme 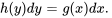
1. En multipliant les deux côtés par 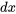 et
et 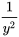 , on obtient
, on obtient
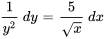
2. En intégrant les deux côtés, on obtient
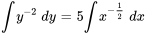
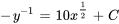
3. En multipliant par -1 et en prenant la réciproque de deux côtés, on obtient la solution explicite
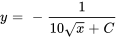
Appliquer la condition initiale :
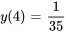
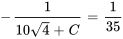
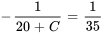
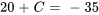
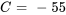
La solution du PVI est donc
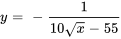
Trouver l’intervalle de validité :
Pour établir l’intervalle de validité de la solution, il faut prendre en considération deux contraintes :
- L’expression contenue dans une racine carrée doit être positive. Par conséquent, le terme sous la racine carrée, doit être supérieur ou égal à 0 (
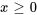 ).
). - Le dénominateur de toute fonction rationnelle ne doit pas être égal à zéro afin d’éviter les expressions indéfinies. Étant donné
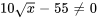 , cela implique que
, cela implique que 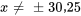 .
.
L’intervalle de validité est la plage des valeurs de  qui satisfont les deux conditions :
qui satisfont les deux conditions :
Prenons un exemple
Section 2.1 Exercices
- Résous l’équation différentielle :
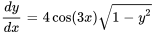
Afficher/Masquer la réponse
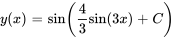
- Résous l’équation différentielle. Exprime
 explicitement en fonction de
explicitement en fonction de  .
.
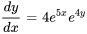
Afficher/Masquer la réponse
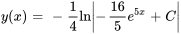
- Résous le problème de valeur initiale :
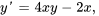
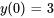
Afficher/Masquer la réponse
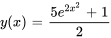
- Résous le problème de valeur initiale et trouver l’intervalle de validité de la solution :
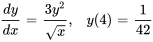
Afficher/Masquer la réponse
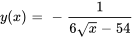
Intervalle de validité :