Chapter 17 – Review

17.1 Chemical Reaction Rates

1. What is the difference between average rate, initial rate, and instantaneous rate? Check Answer: ^[1]
2. Ozone decomposes to oxygen according to the equation [latex]2\text{O}_3(g)\;{\longrightarrow}\;3\text{O}_2(g)[/latex]. Write the equation that relates the rate expressions for this reaction in terms of the disappearance of O₃ and the formation of oxygen.
3. In the nuclear industry, chlorine trifluoride is used to prepare uranium hexafluoride, a volatile compound of uranium used in the separation of uranium isotopes. Chlorine trifluoride is prepared by the reaction [latex]\text{Cl}_2(g)\;+\;3\text{F}_2(g)\;{\longrightarrow}\;2\text{ClF}_3(g)[/latex]. Write the equation that relates the rate expressions for this reaction in terms of the disappearance of Cl₂ and F₂ and the formation of ClF₃. Check Answer: ^[2]
4. A study of the rate of dimerization of C₄H₆ gave the data shown in the table below:
   [latex]2\text{C}_4\text{H}_6\;{\longrightarrow}\;\text{C}_8\text{H}_{12}[/latex]

   Time (s)	0	1600	3200	4800	6200
   [C4H6] (M)	1.00 × 10−2	5.04 × 10−3	3.37 × 10−3	2.53 × 10−3	2.08 × 10−3

   1. Determine the average rate of dimerization between 0 s and 1600 s, and between 1600 s and 3200 s.
   2. Estimate the instantaneous rate of dimerization at 3200 s from a graph of time versus [C₄H₆]. What are the units of this rate?
   3. Determine the average rate of formation of C₈H₁₂ at 1600 s and the instantaneous rate of formation at 3200 s from the rates found in parts (a) and (b).
5. A study of the rate of the reaction represented as [latex]2A\;{\longrightarrow}\;B[/latex] gave the following data as shown in the table below:
   

   Time (s)	0.0	5.0	10.0	15.0	20.0	25.0	35.0
   [A] (M)	1.00	0.952	0.625	0.465	0.370	0.308	0.230

   1. Determine the average rate of disappearance of A between 0.0 s and 10.0 s, and between 10.0 s and 20.0 s.
   2. Estimate the instantaneous rate of disappearance of A at 15.0 s from a graph of time versus [A]. What are the units of this rate?
   3. Use the rates found in parts (a) and (b) to determine the average rate of formation of B between 0.00 s and 10.0 s, and the instantaneous rate of formation of B at 15.0 s.
      Check Answer: ^[3]
6. Consider the following reaction in aqueous solution:
   [latex]5\text{Br}^{-}(aq)\;+\;\text{BrO}_3^{\;\;-}(aq)\;+\;6\text{H}^{+}(aq)\;{\longrightarrow}\;3\text{Br}_2(aq)\;+\;3\text{H}_2\text{O}(l)[/latex]

   If the rate of disappearance of Br^–(aq) at a particular moment during the reaction is 3.5 × 10⁻⁴M s⁻¹, what is the rate of appearance of Br₂(aq) at that moment?

17.2 Chemical Equilibria

1. What does it mean to describe a reaction as “reversible”? Check Answer: ^[4]
2. When writing an equation, how is a reversible reaction distinguished from a nonreversible reaction?
3. If a reaction is reversible, when can it be said to have reached equilibrium? Check Answer: ^[5]
4. Is a system at equilibrium if the rate constants of the forward and reverse reactions are equal?
5. If the concentrations of products and reactants are equal, is the system at equilibrium? Check Answer: ^[6]

1. Explain why there may be an infinite number of values for the reaction quotient of a reaction at a given temperature but there can be only one value for the equilibrium constant at that temperature.
2. Explain why an equilibrium between Br₂(l) and Br₂(g) would not be established if the container were not a closed vessel. Check Answer: ^[7]
3. If you observe the following reaction at equilibrium, is it possible to tell whether the reaction started with pure NO₂ or with pure N₂O₄?
   [latex]2\text{NO}_2(g)\;{\rightleftharpoons}\;\text{N}_2\text{O}_4(g)[/latex]
4. Among the solubility rules previously discussed is the statement: All chlorides are soluble except Hg₂Cl₂, AgCl, PbCl₂, and CuCl.
   1. Write the expression for the equilibrium constant for the reaction represented by the equation [latex]\text{AgCl}(s)\;{\rightleftharpoons}\;\text{Ag}^{+}(aq)\;+\;\text{Cl}^{-}(aq)[/latex]. Is K_c > 1, < 1, or ≈ 1? Explain your answer.
   2. Write the expression for the equilibrium constant for the reaction represented by the equation [latex]\text{Pb}^{2+}(aq)\;+\;2\text{Cl}^{-}(aq)\;{\rightleftharpoons}\;\text{PbCl}_2(s)[/latex]. Is K_c > 1, < 1, or ≈ 1? Explain your answer.
      Check Answer: ^[8]
5. Among the solubility rules previously discussed is the statement: Carbonates, phosphates, borates, and arsenates—except those of the ammonium ion and the alkali metals—are insoluble.
   1. Write the expression for the equilibrium constant for the reaction represented by the equation [latex]\text{CaCO}_3(s)\;{\rightleftharpoons}\;\text{Ca}^{2+}(aq)\;+\;\text{CO}_3^{\;\;-}(aq)[/latex]. Is K_c > 1, < 1, or ≈ 1? Explain your answer.
   2. Write the expression for the equilibrium constant for the reaction represented by the equation [latex]3\text{Ba}^{2+}(aq)\;+\;2\text{PO}_4^{\;\;3-}(aq)\;{\rightleftharpoons}\;\text{Ba}_3(\text{PO}_4)_2(s)[/latex]. Is K_c > 1, < 1, or ≈ 1? Explain your answer.
6. Benzene is one of the compounds used as octane enhancers in unleaded gasoline. It is manufactured by the catalytic conversion of acetylene to benzene: [latex]3\text{C}_2\text{H}_2(g)\;{\longrightarrow}\;\text{C}_6\text{H}_6(g)[/latex]. Which value of K_c would make this reaction most useful commercially? K_c ≈ 0.01, K_c ≈ 1, or K_c ≈ 10. Explain your answer. Check Answer: ^[9]
7. Show that the complete chemical equation, the total ionic equation, and the net ionic equation for the reaction represented by the equation [latex]\text{KI}(aq)\;+\;\text{I}_2(aq)\;{\rightleftharpoons}\;\text{KI}_3(aq)[/latex] give the same expression for the reaction quotient. KI₃ is composed of the ions K⁺ and I₃^–.
8. For a titration to be effective, the reaction must be rapid and the yield of the reaction must essentially be 100%. Is K_c > 1, < 1, or ≈ 1 for a titration reaction? Check Answer: ^[10]
9. For a precipitation reaction to be useful in a gravimetric analysis, the product of the reaction must be insoluble. Is K_c > 1, < 1, or ≈ 1 for a useful precipitation reaction?
10. Write the mathematical expression for the reaction quotient, Q_c, for each of the following reactions:
    1. [latex]\text{CH}_4(g)\;+\;\text{Cl}_2(g)\;{\rightleftharpoons}\;\text{CH}_3\text{Cl}(g)\;+\;\text{HCl}(g)[/latex]
    2. [latex]\text{N}_2(g)\;+\;\text{O}_2(g)\;{\rightleftharpoons}\;2\text{NO}(g)[/latex]
    3. [latex]2\text{SO}_2(g)\;+\;\text{O}_2(g)\;{\rightleftharpoons}\;2\text{SO}_3(g)[/latex]
    4. [latex]\text{BaSO}_3(s)\;{\rightleftharpoons}\;\text{BaO}(s)\;+\;\text{SO}_2(g)[/latex]
    5. [latex]\text{P}_4(g)\;+\;5\text{O}_2(g)\;{\rightleftharpoons}\;\text{P}_4\text{O}_{10}(s)[/latex]
    6. [latex]\text{Br}_2(g)\;{\rightleftharpoons}\;2\text{Br}(g)[/latex]
    7. [latex]\text{CH}_4(g)\;+\;2\text{O}_2(g)\;{\rightleftharpoons}\;\text{CO}_2(g)\;+\;2\text{H}_2\text{O}(l)[/latex]
    8. [latex]\text{CuSO}_4{\cdot}5\text{H}_2\text{O}(s)\;{\rightleftharpoons}\;\text{CuSO}_4(s)\;+\;5\text{H}_2\text{O}(g)[/latex]
       Check Answer: ^[11]
11. Write the mathematical expression for the reaction quotient, Q_c, for each of the following reactions:
    1. [latex]\text{N}_2(g)\;+\;3\text{H}_2(g)\;{\rightleftharpoons}\;2\text{NH}_3(g)[/latex]
    2. [latex]4\text{NH}_3(g)\;+\;5\text{O}_2(g)\;{\rightleftharpoons}\;4\text{NO}(g)\;+\;6\text{H}_2\text{O}(g)[/latex]
    3. [latex]\text{N}_2\text{O}_4(g)\;{\rightleftharpoons}\;2\text{NO}_2(g)[/latex]
    4. [latex]\text{CO}_2(g)\;+\;\text{H}_2(g)\;{\rightleftharpoons}\;\text{CO}(g)\;+\;\text{H}_2\text{O}(g)[/latex]
    5. [latex]\text{NH}_4\text{Cl}(s)\;{\rightleftharpoons}\;\text{NH}_3(g)\;+\;\text{HCl}(g)[/latex]
    6. [latex]2\text{Pb(NO}_3)_2(s)\;{\rightleftharpoons}\;2\text{PbO}(s)\;+\;4\text{NO}_2(g)\;+\;\text{O}_2(g)[/latex]
    7. [latex]2\text{H}_2(g)\;+\;\text{O}_2(g)\;{\rightleftharpoons}\;2\text{H}_2\text{O}(l)[/latex]
    8. [latex]\text{S}_8(g)\;{\rightleftharpoons}\;8\text{S}(g)[/latex]
12. The initial concentrations or pressures of reactants and products are given for each of the following systems. Calculate the reaction quotient and determine the direction in which each system will proceed to reach equilibrium.
    1. [latex]2\text{NH}_3(g)\;{\rightleftharpoons}\;\text{N}_2(g)\;+\;3\text{H}_2(g)\;\;\;\;\;\;\;K_c = 17[/latex]; [NH₃] = 0.20 M, [N₂] = 1.00 M, [H₂] = 1.00 M
    2. [latex]2\text{NH}_3(g)\;{\rightleftharpoons}\;\text{N}_2(g)\;+\;3\text{H}_2(g)\;\;\;\;\;\;\;K_P = 6.8\;\times\;10^4[/latex]; initial pressures: NH₃ = 3.0 atm, N₂ = 2.0 atm, H₂ = 1.0 atm
    3. [latex]2\text{SO}_3(g)\;{\rightleftharpoons}\;2\text{SO}_2(g)\;+\;\text{O}_2(g)\;\;\;\;\;\;\;K_c = 0.230[/latex]; [SO₃] = 0.00 M, [SO₂] = 1.00 M, [O₂] = 1.00 M
    4. [latex]2\text{SO}_3(g)\;{\rightleftharpoons}\;2\text{SO}_2(g)\;+\;\text{O}_2(g)\;\;\;\;\;\;\;K_P = 16.5[/latex]; initial pressures: SO₃ = 1.00 atm, SO₂ = 1.00 atm, O₂ = 1.00 atm
    5. [latex]2\text{NO}(g)\;+\;\text{Cl}_2(g)\;{\rightleftharpoons}\;2\text{NOCl}(g)\;\;\;\;\;\;\;K_c = 4.6\;\times\;10^4[/latex]; [NO] = 1.00 M, [Cl₂] = 1.00 M, [NOCl] = 0 M
    6. [latex]\text{N}_2(g)\;+\;\text{O}_2(g)\;{\rightleftharpoons}\;2\text{NO}(g)\;\;\;\;\;\;\;K_P = 0.050[/latex]; initial pressures: NO = 10.0 atm, N₂ = O₂ = 5 atm
       Check Answer: ^[12]
13. The initial concentrations or pressures of reactants and products are given for each of the following systems. Calculate the reaction quotient and determine the direction in which each system will proceed to reach equilibrium.
    1. [latex]2\text{NH}_3(g)\;{\rightleftharpoons}\;\text{N}_2(g)\;+\;3\text{H}_2(g)\;\;\;\;\;\;\;K_c = 17[/latex]; [NH₃] = 0.50 M, [N₂] = 0.15 M, [H₂] = 0.12 M
    2. [latex]2\text{NH}_3(g)\;{\rightleftharpoons}\;\text{N}_2(g)\;+\;3\text{H}_2(g)\;\;\;\;\;\;\;K_P = 6.8\;\times\;10^4[/latex]; initial pressures: NH₃ = 2.00 atm, N₂ = 10.00 atm, H₂ = 10.00 atm
    3. [latex]2\text{SO}_3(g)\;{\rightleftharpoons}\;2\text{SO}_2(g)\;+\;\text{O}_2(g)\;\;\;\;\;\;\;K_c = 0.230[/latex]; [SO₃] = 2.00 M, [SO₂] = 2.00 M, [O₂] = 2.00 M
    4. [latex]2\text{SO}_3(g)\;{\rightleftharpoons}\;2\text{SO}_2(g)\;+\;\text{O}_2(g)\;\;\;\;\;\;\;K_P = 6.5\;\text{atm}[/latex]; initial pressures: SO₂ = 1.00 atm, O₂ = 1.130 atm, SO₃ = 0 atm
    5. [latex]2\text{NO}(g)\;+\;\text{Cl}_2(g)\;{\rightleftharpoons}\;2\text{NOCl}(g)\;\;\;\;\;\;\;K_P = 2.5\;\times\;10^3[/latex]; initial pressures: NO = 1.00 atm, Cl₂ = 1.00 atm, NOCl = 0 atm
    6. [latex]\text{N}_2(g)\;+\;\text{O}_2(g)\;{\rightleftharpoons}\;2\text{NO}(g)\;\;\;\;\;\;\;K_c = 0.050[/latex]; [N₂] = 0.100 M, [O₂] = 0.200 M, [NO] = 1.00 M
14. The following reaction has K_P = 4.50 × 10⁻⁵ at 720 K.
    [latex]\text{N}_2(g)\;+\;3\text{H}_2(g)\;{\rightleftharpoons}\;2\text{NH}_3(g)[/latex]
    If a reaction vessel is filled with each gas to the partial pressures listed, in which direction will it shift to reach equilibrium? P(NH₃) = 93 atm, P(N₂) = 48 atm, and P(H₂) = 52 Check Answer: ^[13]
15. Determine if the following system is at equilibrium. If not, in which direction will the system need to shift to reach equilibrium?
    [latex]\text{SO}_2\text{Cl}_2(g)\;{\rightleftharpoons}\;\text{SO}_2(g)\;+\;\text{Cl}_2(g)[/latex]
    [SO₂Cl₂] = 0.12 M, [Cl₂] = 0.16 M and [SO₂] = 0.050 M. K_c for the reaction is 0.078.
16. Convert the values of K_c to values of K_P or the values of K_P to values of K_c.
    1. [latex]\text{N}_2(g)\;+\;3\text{H}_2(g)\;{\rightleftharpoons}\;2\text{NH}_3(g)\;\;\;\;\;\;\;K_c = 0.50\;\text{at}\;400\;^{\circ}\text{C}[/latex]
    2. [latex]\text{H}_2\;+\;\text{I}_2\;{\rightleftharpoons}\;2\text{HI}\;\;\;\;\;\;\;K_c = 50.2\;\text{at}\;448\;^{\circ}\text{C}[/latex]
    3. [latex]\text{Na}_2\text{SO}_4{\cdot}10\text{H}_2\text{O}(s)\;{\rightleftharpoons}\;\text{Na}_2\text{SO}_4(s)\;+\;10\text{H}_2\text{O}(g)\;\;\;\;\;\;\;K_P = 4.08\;\times\;10^{-25}\;\text{at}\;25\;^{\circ}\text{C}[/latex]
    4. [latex]\text{H}_2\text{O}(l)\;{\rightleftharpoons}\;\text{H}_2\text{O}(g)\;\;\;\;\;\;\;K_P = 0.122\;\text{at}\;50\;^{\circ}\text{C}[/latex]
       Check Answer: ^[14]
17. Convert the values of K_c to values of K_P or the values of K_P to values of K_c.
    1. [latex]\text{Cl}_2(g)\;+\;\text{Br}_2(g)\;{\rightleftharpoons}\;2\text{BrCl}(g)\;\;\;\;\;\;\;K_c = 4.7\;\times\;10^{-2}\;\text{at}\;25\;^{\circ}\text{C}[/latex]
    2. [latex]2\text{SO}_2(g)\;+\;\text{O}_2(g)\;{\rightleftharpoons}\;2\text{SO}_3(g)\;\;\;\;\;\;\;K_P = 48.2\;\text{at}\;500\;^{\circ}\text{C}[/latex]
    3. [latex]\text{CaCl}_2{\cdot}6\text{H}_2\text{O}(s)\;{\rightleftharpoons}\;\text{CaCl}_2(s)\;+\;6\text{H}_2\text{O}(g)\;\;\;\;\;\;\;K_P = 5.09\;\times\;10^{-44}\;\text{at}\;25\;^{\circ}\text{C}[/latex]
    4. [latex]\text{H}_2\text{O}(l)\;{\rightleftharpoons}\;\text{H}_2\text{O}(g)\;\;\;\;\;\;\;K_P = 0.196\;\text{at}\;60\;^{\circ}\text{C}[/latex]
18. What is the value of the equilibrium constant expression for the change [latex]\text{H}_2\text{O}(l)\;{\rightleftharpoons}\;\text{H}_2\text{O}(g)[/latex] at 30 °C? Check Answer: ^[15]
19. Write the expression of the reaction quotient for the ionization of HOCN in water.
20. Write the reaction quotient expression for the ionization of NH₃ in water.Check Answer: ^[16]
21. What is the approximate value of the equilibrium constant K_P for the change [latex]\text{C}_2\text{H}_5\text{OC}_2\text{H}_5(l)\;{\rightleftharpoons}\;\text{C}_2\text{H}_5\text{OC}_2\text{H}_5(g)[/latex] at 25 °C. (Vapour pressure was described in the previous chapter on liquids and solids; refer back to this chapter to find the relevant information needed to solve this problem.)

1. The following equation represents a reversible decomposition:
   [latex]\text{CaCO}_3(s)\;{\rightleftharpoons}\;\text{CaO}(s)\;+\;\text{CO}_2(g)[/latex]
   Under what conditions will decomposition in a closed container proceed to completion so that no CaCO₃ remains? Check Answer: ^[17]
2. Explain how to recognize the conditions under which changes in pressure would affect systems at equilibrium.
3. What property of a reaction can we use to predict the effect of a change in temperature on the value of an equilibrium constant? Check Answer: ^[18]
4. What would happen to the colour of the solution in part (b) of Figure 17.4a if a small amount of NaOH were added and Fe(OH)₃ precipitated? Explain your answer.
5. The following reaction occurs when a burner on a gas stove is lit:
   [latex]\text{CH}_4(g)\;+\;2\text{O}_2(g)\;{\rightleftharpoons}\;\text{CO}_2(g)\;+\;2\text{H}_2\text{O}(g)[/latex]
   Is an equilibrium among CH₄, O₂, CO₂, and H₂O established under these conditions? Explain your answer. Check Answer: ^[19]
6. A necessary step in the manufacture of sulfuric acid is the formation of sulfur trioxide, SO₃, from sulfur dioxide, SO₂, and oxygen, O₂, shown here. At high temperatures, the rate of formation of SO₃ is higher, but the equilibrium amount (concentration or partial pressure) of SO₃ is lower than it would be at lower temperatures.
   [latex]2\text{SO}_2(g)\;+\;\text{O}_2(g)\;{\longrightarrow}\;2\text{SO}_3(g)[/latex]
   1. Does the equilibrium constant for the reaction increase, decrease, or remain about the same as the temperature increases?
   2. Is the reaction endothermic or exothermic?
7. Suggest four ways in which the concentration of PH₃ could be increased in an equilibrium described by the following equation:
   [latex]\text{P}_4(g)\;+\;6\text{H}_2(g)\;{\rightleftharpoons}\;4\text{PH}_3(g)\;\;\;\;\;\;\;{\Delta}H = 110.5\;\text{kJ}[/latex]
   Check Answer: ^[20]
8. Water gas is a 1:1 mixture of carbon monoxide and hydrogen gas and is called water gas because it is formed from steam and hot carbon in the following reaction: [latex]\text{H}_2\text{O}(g)\;+\;\text{C}(s)\;{\rightleftharpoons}\;\text{H}_2(g)\;+\;\text{CO}(g)[/latex]. Methanol, a liquid fuel that could possibly replace gasoline, can be prepared from water gas and hydrogen at high temperature and pressure in the presence of a suitable catalyst.
   1. Write the expression for the equilibrium constant (K_c) for the reversible reaction
      [latex]2\text{H}_2(g)\;+\;\text{CO}(g)\;{\rightleftharpoons}\;\text{CH}_3\text{OH}(g)\;\;\;\;\;\;\;{\Delta}H = -90.2\;\text{kJ}[/latex]
   2. What will happen to the concentrations of H₂, CO, and CH₃OH at equilibrium if more H₂ is added?
   3. What will happen to the concentrations of H₂, CO, and CH₃OH at equilibrium if CO is removed?
   4. What will happen to the concentrations of H₂, CO, and CH₃OH at equilibrium if CH₃OH is added?
   5. What will happen to the concentrations of H₂, CO, and CH₃OH at equilibrium if the temperature of the system is increased?
   6. What will happen to the concentrations of H₂, CO, and CH₃OH at equilibrium if more catalyst is added?
9. Nitrogen and oxygen react at high temperatures.
   1. Write the expression for the equilibrium constant (K_c) for the reversible reaction
      [latex]\text{N}_2(g)\;+\;\text{O}_2(g)\;{\rightleftharpoons}\;2\text{NO}(g)\;\;\;\;\;\;\;{\Delta}H = 181\;\text{kJ}[/latex]
   2. What will happen to the concentrations of N₂, O₂, and NO at equilibrium if more O₂ is added?
   3. What will happen to the concentrations of N₂, O₂, and NO at equilibrium if N₂ is removed?
   4. What will happen to the concentrations of N₂, O₂, and NO at equilibrium if NO is added?
   5. What will happen to the concentrations of N₂, O₂, and NO at equilibrium if the pressure on the system is increased by reducing the volume of the reaction vessel?
   6. What will happen to the concentrations of N₂, O₂, and NO at equilibrium if the temperature of the system is increased?
   7. What will happen to the concentrations of N₂, O₂, and NO at equilibrium if a catalyst is added?
      Check Answer:
10. Water gas, a mixture of H₂ and CO, is an important industrial fuel produced by the reaction of steam with red hot coke, essentially pure carbon.
    1. Write the expression for the equilibrium constant for the reversible reaction
       [latex]\text{C}(s)\;+\;\text{H}_2\text{O}(g)\;{\rightleftharpoons}\;\text{CO}(g)\;+\;\text{H}_2(g)\;\;\;\;\;\;\;{\Delta}H = 131.30\;\text{kJ}[/latex]
    2. What will happen to the concentration of each reactant and product at equilibrium if more C is added?
    3. What will happen to the concentration of each reactant and product at equilibrium if H₂O is removed?
    4. What will happen to the concentration of each reactant and product at equilibrium if CO is added?
    5. What will happen to the concentration of each reactant and product at equilibrium if the temperature of the system is increased?
11. Pure iron metal can be produced by the reduction of iron(III) oxide with hydrogen gas.
    1. Write the expression for the equilibrium constant (K_c) for the reversible reaction
       [latex]\text{Fe}_2\text{O}_3(s)\;+\;3\text{H}_2(g)\;{\rightleftharpoons}\;2\text{Fe}(s)\;+\;3\text{H}_2\text{O}(g)\;\;\;\;\;\;\;{\Delta}H = 98.7\;\text{kJ}[/latex]
    2. What will happen to the concentration of each reactant and product at equilibrium if more Fe is added?
    3. What will happen to the concentration of each reactant and product at equilibrium if H₂O is removed?
    4. What will happen to the concentration of each reactant and product at equilibrium if H₂ is added?
    5. What will happen to the concentration of each reactant and product at equilibrium if the pressure on the system is increased by reducing the volume of the reaction vessel?
    6. What will happen to the concentration of each reactant and product at equilibrium if the temperature of the system is increased?
       Check Answer: ^[21]
12. Ammonia is a weak base that reacts with water according to this equation:
    [latex]\text{NH}_3(aq)\;+\;\text{H}_2\text{O}(l)\;{\rightleftharpoons}\;\text{NH}_4^{\;\;+}(aq)\;+\;\text{OH}^{-}(aq)[/latex]
    Will any of the following increase the percent of ammonia that is converted to the ammonium ion in water?
    1. Addition of NaOH
    2. Addition of HCl
    3. Addition of NH₄Cl
13. Acetic acid is a weak acid that reacts with water according to this equation:
    [latex]\text{CH}_3\text{CO}_2\text{H}(aq)\;+\;\text{H}_2\text{O}(aq)\;{\rightleftharpoons}\;\text{H}_3\text{O}^{+}(aq)\;+\;\text{CH}_3\text{CO}_2^{\;\;-}(aq)[/latex]
    Will any of the following increase the percent of acetic acid that reacts and produces CH₃CO₂^– ion?
    1. Addition of HCl
    2. Addition of NaOH
    3. Addition of NaCH₃CO₂
       Check Answer: ^[22]
14. Suggest two ways in which the equilibrium concentration of Ag⁺ can be reduced in a solution of Na⁺, Cl⁻, Ag⁺, and NO₃^– , in contact with solid AgCl.
    [latex]\text{Na}^{+}(aq)\;+\;\text{Cl}^{-}(aq)\;+\;\text{Ag}^{+}(aq)\;+\;\text{NO}_3^{\;\;-}(aq)\;{\rightleftharpoons}\;\text{AgCl}(s)\;+\;\text{Na}^{+}(aq)\;+\;\text{NO}_3^{\;\;-}(aq)[/latex]
    [latex]{\Delta}H = -65.9\;\text{kJ}[/latex]
15. How can the pressure of water vapor be increased in the following equilibrium?
    [latex]\text{H}_2\text{O}(l)\;{\rightleftharpoons}\;\text{H}_2\text{O}(g)\;\;\;\;\;\;\;{\Delta}H = 41\;\text{kJ}[/latex]
    Check Answer: ^[23]
16. Additional solid silver sulfate, a slightly soluble solid, is added to a solution of silver ion and sulfate ion at equilibrium with solid silver sulfate.
    [latex]2\text{Ag}^{+}(aq)\;+\;\text{SO}_4^{\;\;2-}(aq)\;{\rightleftharpoons}\;\text{Ag}_2\text{SO}_4(s)[/latex]
    Which of the following will occur?
    1. Ag⁺ or SO₄^2- concentrations will not change.
    2. The added silver sulfate will dissolve.
    3. Additional silver sulfate will form and precipitate from solution as Ag⁺ ions and SO₄^2- ions combine.
    4. The Ag⁺ ion concentration will increase and the SO₄^2- ion concentration will decrease.
17. The amino acid alanine has two isomers, α-alanine and β-alanine. When equal masses of these two compounds are dissolved in equal amounts of a solvent, the solution of α-alanine freezes at the lowest temperature. Which form, α-alanine or β-alanine, has the larger equilibrium constant for ionization [latex](\text{HX}\;{\rightleftharpoons}\;\text{H}^{+}\;+\;\text{X}^{-})[/latex]?
    Check Answer: ^[24]

1. A reaction is represented by this equation: [latex]\text{A}(aq)\;+\;2\text{B}(aq)\;{\rightleftharpoons}\;2\text{C}(aq)\;\;\;\;\;\;\;K_c = 1\;\times\;10^3[/latex]
   1. Write the mathematical expression for the equilibrium constant.
   2. Using concentrations ≤1 M, make up two sets of concentrations that describe a mixture of A, B, and C at equilibrium.
      Check Answer: ^[25]
2. A reaction is represented by this equation: [latex]2\text{W}(aq)\;{\rightleftharpoons}\;\text{X}(aq)\;+\;2\text{Y}(aq)\;\;\;\;\;\;\;K_c = 5\;\times\;10^{-4}[/latex]
   1. Write the mathematical expression for the equilibrium constant.
   2. Using concentrations of ≤1 M, make up two sets of concentrations that describe a mixture of W, X, and Y at equilibrium.
3. What is the value of the equilibrium constant at 500 °C for the formation of NH₃ according to the following equation?
   [latex]\text{N}_2(g)\;+\;3\text{H}_2(g)\;{\rightleftharpoons}\;2\text{NH}_3(g)[/latex]
   An equilibrium mixture of NH₃(g), H₂(g), and N₂(g) at 500 °C was found to contain 1.35 M H₂, 1.15 M N₂, and 4.12 × 10⁻¹M NH₃.
   Check Answer: ^[26]
4. Hydrogen is prepared commercially by the reaction of methane and water vapour at elevated temperatures.
   [latex]\text{CH}_4(g)\;+\;\text{H}_2\text{O}(g)\;{\rightleftharpoons}\;3\text{H}_2(g)\;+\;\text{CO}(g)[/latex]
   What is the equilibrium constant for the reaction if a mixture at equilibrium contains gases with the following concentrations: CH₄, 0.126 M; H₂O, 0.242 M; CO, 0.126 M; H₂ 1.15 M, at a temperature of 760 °C?
5. A 0.72-mol sample of PCl₅ is put into a 1.00-L vessel and heated. At equilibrium, the vessel contains 0.40 mol of PCl₃(g) and 0.40 mol of Cl₂(g). Calculate the value of the equilibrium constant for the decomposition of PCl₅ to PCl₃ and Cl₂ at this temperature. Check Answer: ^[27]
6. At 1 atm and 25 °C, NO₂ with an initial concentration of 1.00 M is 3.3 × 10⁻³% decomposed into NO and O₂. Calculate the value of the equilibrium constant for the reaction.
   [latex]2\text{NO}_2(g)\;{\rightleftharpoons}\;2\text{NO}(g)\;+\;\text{O}_2(g)[/latex]
7. Calculate the value of the equilibrium constant K_P for the reaction [latex]2\text{NO}(g)\;+\;\text{Cl}_2(g)\;{\rightleftharpoons}\;2\text{NOCl}(g)[/latex] from these equilibrium pressures: NO, 0.050 atm; Cl₂, 0.30 atm; NOCl, 1.2 atm. Check Answer: ^[28]
8. When heated, iodine vapor dissociates according to this equation:
   [latex]\text{I}_2(g)\;{\rightleftharpoons}\;2\text{I}(g)[/latex]
   At 1274 K, a sample exhibits a partial pressure of I₂ of 0.1122 atm and a partial pressure due to I atoms of 0.1378 atm. Determine the value of the equilibrium constant, K_P, for the decomposition at 1274 K.
9. A sample of ammonium chloride was heated in a closed container.
   [latex]\text{NH}_4\text{Cl}(s)\;{\rightleftharpoons}\;\text{NH}_3(g)\;+\;\text{HCl}(g)[/latex]
   At equilibrium, the pressure of NH₃(g) was found to be 1.75 atm. What is the value of the equilibrium constant K_P for the decomposition at this temperature? Check Answer: ^[29]
10. At a temperature of 60 °C, the vapour pressure of water is 0.196 atm. What is the value of the equilibrium constant K_P for the transformation at 60 °C?
    [latex]\text{H}_2\text{O}(l)\;{\rightleftharpoons}\;\text{H}_2\text{O}(g)[/latex]
11. Complete the changes in concentrations (or pressure, if requested) for each of the following reactions in the table below.
    

    a.		2 SO3 (g)	[latex]{\rightleftharpoons}[/latex]	2 SO2 (g)	+ O2 (g)
    		______		______	+x
    		______		______	0.125 M
    b.	4 NH3 (g)	+ 3 O2 (g)	[latex]{\rightleftharpoons}[/latex]	2 N2 (g)	+ 6 H2O (g)
    	______	3x		______	______
    	______	0.24 M		______	______
    c.		2 CH4 (g)	[latex]{\rightleftharpoons}[/latex]	C2H2 (g)	+ 3 H2 (g)
    		______		x	______
    		______		25 torr	______
    d.	CH4 (g)	+ H2O (g)	[latex]{\rightleftharpoons}[/latex]	CO (g)	+ 3 H2 (g)
    	______	x		______	______
    	______	5 atm		______	______
    e.		NH4Cl (s)	[latex]{\rightleftharpoons}[/latex]	NH3 (g)	+ HCl (g)
    				x	______
    				1.03 x 10-4 M	______
    f.	Ni (s)	+ 4 CO (g)	[latex]{\rightleftharpoons}[/latex]	Ni(CO)4 (g)
    		4x		______
    		0.40 atm		______

    Check Answer: ^[30]

12. Complete the changes in concentrations (or pressure, if requested) for each of the following reactions in the table below.
    

    a.	2 H2 (g)	+ O2 (g)	[latex]{\rightleftharpoons}[/latex]	2 H2O (g)
    	______	______		+2x
    	______	______		1.50 M
    b.	CS2 (g)	+ 4 H2 (g)	[latex]{\rightleftharpoons}[/latex]	CH4 (g)	+ 2 H2S (g)
    	x	______		______	______
    	0.020 M	______		______	______
    c.	H2 (g)	+ Cl2 (g)	[latex]{\rightleftharpoons}[/latex]	2 HCl (g)
    	x	______		______
    	1.50 atm	______		______
    d.	2 NH3 (g)	+ 2 O2 (g)	[latex]{\rightleftharpoons}[/latex]	N2O (g)	+ 3 H2O (g)
    	______	______		______	x
    	______	______		______	60.6 torr
    e.		NH4HS (s)	[latex]{\rightleftharpoons}[/latex]	NH3 (g)	+ H2S (g)
    				x	______
    				9.8 x 10-6 M	______
    f.	Fe (s)	+ 5 CO (g)	[latex]{\rightleftharpoons}[/latex]	Fe(CO)4 (g)
    		______		x
    		______		0.012 atm

13. Why are there no changes specified for Ni in Exercise 11, part (f) above? What property of Ni does change? Check Answer: ^[31]
14. Why are there no changes specified for NH₄HS in Exercise 12, part (e) above? What property of NH₄HS does change?
15. Analysis of the gases in a sealed reaction vessel containing NH₃, N₂, and H₂ at equilibrium at 400 °C established the concentration of N₂ to be 1.2 M and the concentration of H₂ to be 0.24 M.
    [latex]\text{N}_2(g)\;+\;3\text{H}_2(g)\;{\rightleftharpoons}\;2\text{NH}_3(g)\;\;\;\;\;\;\;K_c = 0.50\;\text{at}\;400\;^{\circ}\text{C}[/latex]
    Calculate the equilibrium molar concentration of NH₃. Check Answer: ^[32]
16. Calculate the number of moles of HI that are at equilibrium with 1.25 mol of H₂ and 1.25 mol of I₂ in a 5.00−L flask at 448 °C.
    [latex]\text{H}_2\;+\;\text{I}_2\;{\rightleftharpoons}\;2\text{HI}\;\;\;\;\;\;\;K_c = 50.2\;\text{at}\;448\;^{\circ}\text{C}[/latex]
17. What is the pressure of BrCl in an equilibrium mixture of Cl₂, Br₂, and BrCl if the pressure of Cl₂ in the mixture is 0.115 atm and the pressure of Br₂ in the mixture is 0.450 atm?
    [latex]\text{Cl}_2(g)\;+\;\text{Br}_2(g)\;{\rightleftharpoons}\;2\text{BrCl}(g)\;\;\;\;\;\;\;K_P = 4.7\;\times\;10^{-2}[/latex]
    Check Answer: ^[33]
18. What is the pressure of CO₂ in a mixture at equilibrium that contains 0.50 atm H₂, 2.0 atm of H₂O, and 1.0 atm of CO at 990 °C?
    [latex]\text{H}_2(g)\;+\;\text{CO}_2(g)\;{\rightleftharpoons}\;\text{H}_2\text{O}(g)\;+\;\text{CO}(g)\;\;\;\;\;\;\;K_P = 1.6\;\text{at}\;990\;^{\circ}\text{C}[/latex]
19. Cobalt metal can be prepared by reducing cobalt(II) oxide with carbon monoxide.
    [latex]\text{CoO}(s)\;+\;\text{CO}(g)\;{\rightleftharpoons}\;\text{Co}(s)\;+\;\text{CO}_2(g)\;\;\;\;\;\;\;K_c = 4.90\;\times\;10^2\;\text{at}\;550\;^{\circ}\text{C}[/latex]
    What concentration of CO remains in an equilibrium mixture with [CO₂] = 0.100 M? Check Answer: ^[34]
20. Carbon reacts with water vapour at elevated temperatures.
    [latex]\text{C}(s)\;+\;\text{H}_2\text{O}(g)\;{\rightleftharpoons}\;\text{CO}(g)\;+\;\text{H}_2(g)\;\;\;\;\;\;\;K_c = 0.2\;\text{at}\;1000\;^{\circ}\text{C}[/latex]
    What is the concentration of CO in an equilibrium mixture with [H₂O] = 0.500 M at 1000 °C?
21. Sodium sulfate 10−hydrate, Na₂SO₄·10H₂O, dehydrates according to the equation
    [latex]\text{Na}_2\text{SO}_4{\cdot}10\text{H}_2\text{O}(s)\;{\rightleftharpoons}\;\text{Na}_2\text{SO}_4(s)\;+\;10\text{H}_2\text{O}(g)\;\;\;\;\;\;\;K_P = 4.08\;\times\;10^{-25}\;\text{at}\;25\;^{\circ}\text{C}[/latex]
    What is the pressure of water vapour at equilibrium with a mixture of Na₂SO₄·10H₂O and NaSO₄? Check Answer: ^[35]
22. Calcium chloride 6−hydrate, CaCl₂·6H₂O, dehydrates according to the equation
    [latex]\text{CaCl}_2{\cdot}6\text{H}_2\text{O}(s)\;{\rightleftharpoons}\;\text{CaCl}_2(s)\;+\;6\text{H}_2\text{O}(g)\;\;\;\;\;\;\;K_P = 5.09\;\times\;10^{-44}\;\text{at}\;25\;^{\circ}\text{C}[/latex]
    What is the pressure of water vapour at equilibrium with a mixture of CaCl₂·6H₂O and CaCl₂?
23. A student solved the following problem and found the equilibrium concentrations to be [SO₂] = 0.590 M, [O₂] = 0.0450 M, and [SO₃] = 0.260 M. How could this student check the work without reworking the problem? The problem was: For the following reaction at 600 °C:
    [latex]2\text{SO}_2(g)\;+\;\text{O}_2(g)\;{\rightleftharpoons}\;2\text{SO}_3(g)\;\;\;\;\;\;\;K_c = 4.32[/latex]
    What are the equilibrium concentrations of all species in a mixture that was prepared with [SO₃] = 0.500 M, [SO₂] = 0 M, and [O₂] = 0.350 M? Check Answer: ^[36]
24. A student solved the following problem and found [N₂O₄] = 0.16 M at equilibrium. How could this student recognize that the answer was wrong without reworking the problem? The problem was: What is the equilibrium concentration of N₂O₄ in a mixture formed from a sample of NO₂ with a concentration of 0.10 M?
    [latex]2\text{NO}_2(g)\;{\rightleftharpoons}\;\text{N}_2\text{O}_4(g)\;\;\;\;\;\;\;K_c = 160[/latex]
25. Assume that the change in concentration of N₂O₄ is small enough to be neglected in the following problem.
    1. Calculate the equilibrium concentration of both species in 1.00 L of a solution prepared from 0.129 mol of N₂O₄ with chloroform as the solvent.
       [latex]\text{N}_2\text{O}_4(g)\;{\leftrightharpoons}\;2\text{NO}_2(g)\;\;\;\;\;\;\;K_c = 1.07\;\times\;10^{-5}[/latex] in chloroform
    2. Show that the change is small enough to be neglected.
       Check Answer: ^[37]
26. Assume that the change in concentration of COCl₂ is small enough to be neglected in the following problem.
    1. Calculate the equilibrium concentration of all species in an equilibrium mixture that results from the decomposition of COCl₂ with an initial concentration of 0.3166 M.
       [latex]\text{COCl}_2(g)\;{\rightleftharpoons}\;\text{CO}(g)\;+\;\text{Cl}_2(g)\;\;\;\;\;\;\;K_c = 2.2\;\times\;10^{-10}[/latex]
    2. Show that the change is small enough to be neglected.
27. Assume that the change in pressure of H₂S is small enough to be neglected in the following problem.
    1. Calculate the equilibrium pressures of all species in an equilibrium mixture that results from the decomposition of H₂S with an initial pressure of 0.824 atm.
       [latex]2\text{H}_2\text{S}(g)\;{\rightleftharpoons}\;2\text{H}_2(g)\;+\;\text{S}_2(g)\;\;\;\;\;\;\;K_P = 2.2\;\times\;10^{-6}[/latex]
    2. Show that the change is small enough to be neglected. Check Answer: ^[38]
28. What are all concentrations after a mixture that contains [H₂O] = 1.00 M and [Cl₂O] = 1.00 M comes to equilibrium at 25 °C?
    [latex]\text{H}_2\text{O}(g)\;+\;\text{Cl}_2\text{O}(g)\;{\rightleftharpoons}\;2\text{HOCl}(g)\;\;\;\;\;\;\;K_c = 0.0900[/latex]
29. What are the concentrations of PCl₅, PCl₃, and Cl₂ in an equilibrium mixture produced by the decomposition of a sample of pure PCl₅ with [PCl₅] = 2.00 M?
    [latex]\text{PCl}_5(g)\;{\rightleftharpoons}\;\text{PCl}_3(g)\;+\;\text{Cl}_2(g)\;\;\;\;\;\;\;K_c = 0.0211[/latex]
    Check Answer: ^[39]
30. Calculate the pressures of all species at equilibrium in a mixture of NOCl, NO, and Cl₂ produced when a sample of NOCl with a pressure of 10.0 atm comes to equilibrium according to this reaction:
    [latex]2\text{NOCl}(g)\;{\rightleftharpoons}\;2\text{NO}(g)\;+\;\text{Cl}_2(g)\;\;\;\;\;\;\;K_P = 4.0\;\times\;10^{-4}[/latex]
31. Calculate the equilibrium concentrations of NO, O₂, and NO₂ in a mixture at 250 °C that results from the reaction of 0.20 M NO and 0.10 M O₂. (Hint: K is large; assume the reaction goes to completion then comes back to equilibrium.) Check Answer: ^[40]
    [latex]2\text{NO}(g)\;+\;\text{O}_2(g)\;{\rightleftharpoons}\;2\text{NO}_2(g)\;\;\;\;\;\;\;K_c = 2.3\;\times\;10^5\;\text{at}\;250\;^{\circ}\text{C}[/latex]
32. Calculate the equilibrium concentrations that result when 0.25 M O₂ and 1.0 M HCl react and come to equilibrium.
    [latex]4\text{HCl}(g)\;+\;\text{O}_2(g)\;{\rightleftharpoons}\;2\text{Cl}_2(g)\;+\;2\text{H}_2\text{O}(g)\;\;\;\;\;\;\;K_c = 3.1\;\times\;10^{13}[/latex]
33. One of the important reactions in the formation of smog is represented by the equation
    [latex]\text{O}_3(g)\;+\;\text{NO}(g)\;{\rightleftharpoons}\;\text{NO}_2(g)\;+\;\text{O}_2(g)\;\;\;\;\;\;\;K_P = 6.0\;\times\;10^{34}[/latex]
    What is the pressure of O₃ remaining after a mixture of O₃ with a pressure of 1.2 × 10⁻⁸ atm and NO with a pressure of 1.2 × 10⁻⁸ atm comes to equilibrium? (Hint: K_P is large; assume the reaction goes to completion then comes back to equilibrium.) Check Answer: ^[41]
34. Calculate the pressures of NO, Cl₂, and NOCl in an equilibrium mixture produced by the reaction of a starting mixture with 4.0 atm NO and 2.0 atm Cl₂. (Hint: K_P is small; assume the reverse reaction goes to completion then comes back to equilibrium.)
    [latex]2\text{NO}(g)\;+\;\text{Cl}_2(g)\;{\rightleftharpoons}\;2\text{NOCl}(g)\;\;\;\;\;\;\;K_P = 2.5\;\times\;10^3[/latex]
35. Calculate the number of grams of HI that are at equilibrium with 1.25 mol of H₂ and 63.5 g of iodine at 448 °C.
    [latex]\text{H}_2\;+\;\text{I}_2\;{\rightleftharpoons}\;2\text{HI}\;\;\;\;\;\;\;K_c = 50.2\;\text{at}\;448\;^{\circ}\text{C}[/latex]
    Check Answer: ^[42]
36. Butane exists as two isomers, n−butane and isobutane shown in the figure below with K_P = 2.5 at 25 °C. 
    

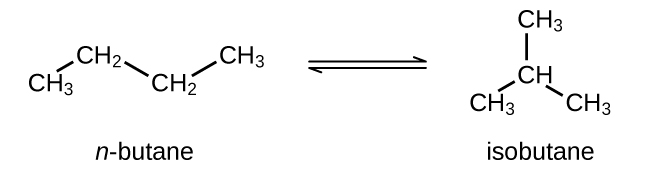
    What is the pressure of isobutane in a container of the two isomers at equilibrium with a total pressure of 1.22 atm?

37. What is the minimum mass of CaCO₃ required to establish equilibrium at a certain temperature in a 6.50-L container if the equilibrium constant (K_c) is 0.050 for the decomposition reaction of CaCO₃ at that temperature?
    [latex]\text{CaCO}_3(s)\;{\rightleftharpoons}\;\text{CaO}(s)\;+\;\text{CO}_2(g)[/latex]
    Check Answer: ^[43]
38. The equilibrium constant (K_c) for this reaction is 1.60 at 990 °C:
    [latex]\text{H}_2(g)\;+\;\text{CO}_2(g)\;{\rightleftharpoons}\;\text{H}_2\text{O}(g)\;+\;\text{CO}(g)[/latex]
    Calculate the number of moles of each component in the final equilibrium mixture obtained from adding 1.00 mol of H₂, 2.00 mol of CO₂, 0.750 mol of H₂O, and 1.00 mol of CO to a 5.00-L container at 990 °C.
39. At 25 °C and at 1 atm, the partial pressures in an equilibrium mixture of N₂O₄ and NO₂ are [latex]\text{P}_{\text{N}_2\text{O}_4} = 0.70\;\text{atm}[/latex] and [latex]\text{P}_{\text{NO}_2} = 0.30\;\text{atm}[/latex].
    1. Predict how the pressures of NO₂ and N₂O₄ will change if the total pressure increases to 9.0 atm. Will they increase, decrease, or remain the same?
    2. Calculate the partial pressures of NO₂ and N₂O₄ when they are at equilibrium at 9.0 atm and 25 °C. Check Answer: ^[44]
40. In a 3.0-L vessel, the following equilibrium partial pressures are measured: N₂, 190 torr; H₂, 317 torr; NH₃, 1.00 × 10³ torr.
    [latex]\text{N}_2(g)\;+\;3\text{H}_2(g)\;{\rightleftharpoons}\;2\text{NH}_3(g)[/latex]
    1. How will the partial pressures of H₂, N₂, and NH₃ change if H₂ is removed from the system? Will they increase, decrease, or remain the same?
    2. Hydrogen is removed from the vessel until the partial pressure of nitrogen, at equilibrium, is 250 torr. Calculate the partial pressures of the other substances under the new conditions.
41. The equilibrium constant (K_c) for this reaction is 5.0 at a given temperature.
    [latex]\text{CO}(g)\;+\;\text{H}_2\text{O}(g)\;{\rightleftharpoons}\;\text{CO}_2(g)\;+\;\text{H}_2(g)[/latex]
    1. On analysis, an equilibrium mixture of the substances present at the given temperature was found to contain 0.20 mol of CO, 0.30 mol of water vapour, and 0.90 mol of H₂ in a litre. How many moles of CO₂ were there in the equilibrium mixture?
    2. Maintaining the same temperature, additional H₂ was added to the system, and some water vapour was removed by drying. A new equilibrium mixture was thereby established containing 0.40 mol of CO, 0.30 mol of water vapour, and 1.2 mol of H₂ in a litre. How many moles of CO₂ were in the new equilibrium mixture? Compare this with the quantity in part (a), and discuss whether the second value is reasonable. Explain how it is possible for the water vapour concentration to be the same in the two equilibrium solutions even though some vapour was removed before the second equilibrium was established. Check Answer: ^[45]
42. Antimony pentachloride decomposes according to this equation:
    [latex]\text{SbCl}_5(g)\;{\rightleftharpoons}\;\text{SbCl}_3(g)\;+\;\text{Cl}_2(g)[/latex]
    An equilibrium mixture in a 5.00-L flask at 448 °C contains 3.85 g of SbCl₅, 9.14 g of SbCl₃, and 2.84 g of Cl₂. How many grams of each will be found if the mixture is transferred into a 2.00-L flask at the same temperature?
43. Consider the reaction between H₂ and O₂ at 1000 K
    [latex]2\text{H}_2(g)\;+\;\text{O}_2(g)\;{\rightleftharpoons}\;2\text{H}_2\text{O}(g)\;\;\;\;\;\;\;K_P = \frac{(P_{\text{H}_2\text{O}})^2}{(P_{\text{O}_2})(P_{\text{H}_2})^3} = 1.33\;\times\;10^{20}[/latex]
    If 0.500 atm of H₂ and 0.500 atm of O₂ are allowed to come to equilibrium at this temperature, what are the partial pressures of the components?  Check Answer: ^[46]
44. An equilibrium is established according to the following equation
    [latex]\text{Hg}_2^{\;\;2+}(aq)\;+\;\text{NO}_3^{\;\;-}(aq)\;+\;3\text{H}^{+}(aq)\;{\rightleftharpoons}\;2\text{Hg}^{2+}(aq)\;+\;\text{HNO}_2(aq)\;+\;\text{H}_2\text{O}(l)\;\;\;\;\;\;\;K_c = 4.6[/latex]
    What will happen in a solution that is 0.20 M each in Hg₂²⁺, NO₃^–, H⁺, Hg²⁺, and HNO₂?
    1. Hg₂²⁺ will be oxidized and NO₃^– reduced.
    2. Hg₂²⁺ will be reduced and NO₃^– oxidized.
    3. Hg²⁺ will be oxidized and HNO₂ reduced.
    4. Hg²⁺ will be reduced and HNO₂ oxidized.
    5. There will be no change because all reactants and products have an activity of 1.
45. Consider the equilibrium
    [latex]4\text{NO}_2(g)\;+\;6\text{H}_2\text{O}(g)\;{\rightleftharpoons}\;4\text{NH}_3(g)\;+\;7\text{O}_2(g)[/latex]
    1. What is the expression for the equilibrium constant (K_c) of the reaction?
    2. How must the concentration of NH₃ change to reach equilibrium if the reaction quotient is less than the equilibrium constant?
    3. If the reaction were at equilibrium, how would a decrease in pressure (from an increase in the volume of the reaction vessel) affect the pressure of NO₂?
    4. If the change in the pressure of NO₂ is 28 torr as a mixture of the four gases reaches equilibrium, how much will the pressure of O₂ change? Check Answer: ^[47]
46. The binding of oxygen by hemoglobin (Hb), giving oxyhemoglobin (HbO₂), is partially regulated by the concentration of H₃O⁺ and dissolved CO₂ in the blood. Although the equilibrium is complicated, it can be summarized as
    [latex]\text{HbO}_2(aq)\;+\;\text{H}_3\text{O}^{+}(aq)\;+\;\text{CO}_2(g)\;{\rightleftharpoons}\;\text{CO}_2\;-\;\text{Hb}\;-\;\text{H}^{+}\;+\;\text{O}_2(g)\;+\;\text{H}_2\text{O}(l)[/latex]
    1. Write the equilibrium constant expression for this reaction.
    2. Explain why the production of lactic acid and CO₂ in a muscle during exertion stimulates release of O₂ from the oxyhemoglobin in the blood passing through the muscle.
47. The hydrolysis of the sugar sucrose to the sugars glucose and fructose follows a first-order rate equation for the disappearance of sucrose.

    [latex]\text{C}_{12}\text{H}_{22}\text{O}_{11}(aq)\;+\;\text{H}_2\text{O}(l)\;{\longrightarrow}\;\text{C}_6\text{H}_{12}\text{O}_6(aq)\;+\;\text{C}_6\text{H}_{12}\text{O}_6(aq)[/latex]

    Rate = k[C₁₂H₂₂O₁₁]

    In neutral solution, k = 2.1 × 10⁻¹¹/s at 27 °C. (As indicated by the rate constant, this is a very slow reaction. In the human body, the rate of this reaction is sped up by a type of catalyst called an enzyme.) (Note: That is not a mistake in the equation—the products of the reaction, glucose and fructose, have the same molecular formulas, C₆H₁₂O₆, but differ in the arrangement of the atoms in their molecules). The equilibrium constant for the reaction is 1.36 × 10⁵ at 27 °C. What are the concentrations of glucose, fructose, and sucrose after a 0.150 M aqueous solution of sucrose has reached equilibrium? Remember that the activity of a solvent (the effective concentration) is 1. Check Answer: ^[48]

48. The density of trifluoroacetic acid vapour was determined at 118.1 °C and 468.5 torr, and found to be 2.784 g/L. Calculate K_c for the association of the acid shown in the figure below.
    
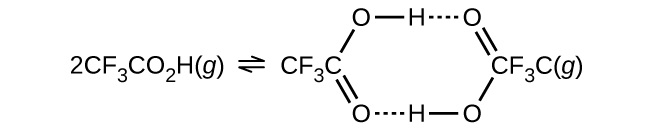
49. Liquid N₂O₃ is dark blue at low temperatures, but the colour fades and becomes greenish at higher temperatures as the compound decomposes to NO and NO₂. At 25 °C, a value of K_P = 1.91 has been established for this decomposition. If 0.236 moles of N₂O₃ are placed in a 1.52-L vessel at 25 °C, calculate the equilibrium partial pressures of N₂O₃(g), NO₂(g), and NO(g).
    Check Answer: ^[49]
50. A 1.00-L vessel at 400 °C contains the following equilibrium concentrations: N₂, 1.00 M; H₂, 0.50 M; and NH₃, 0.25 M. How many moles of hydrogen must be removed from the vessel to increase the concentration of nitrogen to 1.1 M?
51. A 0.010 M solution of the weak acid HA has an osmotic pressure (see chapter on solutions and colloids) of 0.293 atm at 25 °C. A 0.010 M solution of the weak acid HB has an osmotic pressure of 0.345 atm under the same conditions.
    1. Which acid has the larger equilibrium constant for ionization
       HA [latex][\text{HA}(aq)\;{\rightleftharpoons}\;\text{A}^{-}(aq)\;+\;\text{H}^{+}(aq)][/latex] or HB [latex][\text{HB}(aq)\;{\rightleftharpoons}\;\text{H}^{+}(aq)\;+\;\text{B}^{-}(aq)][/latex]?
    2. What are the equilibrium constants for the ionization of these acids?

       (Hint: Remember that each solution contains three dissolved species: the weak acid (HA or HB), the conjugate base (A⁻ or B⁻), and the hydrogen ion (H⁺). Remember that osmotic pressure (like all colligative properties) is related to the total number of solute particles. Specifically for osmotic pressure, those concentrations are described by molarities.) Check Answer: ^[50]

1. Complete the changes in concentrations for each of the following reactions in the table below:
   

   a.	AgI (s)	→	Ag+ (aq)	+ I– (aq)
   			x	______
   b.	CaCO3 (s)	→	Ca2+ (aq)	+ CO32- (aq)
   			______	x
   c.	Mg(OH)2 (s)	→	Mg2+ (aq)	+ 2 OH– (aq)
   			x	______
   d.	Mg3(PO4)2 (s)	→	3 Mg2+ (aq)	+ 2 PO43- (aq)
   			______	2x
   e.	Ca5(PO4)3OH (s)	→	5 Ca2+ (aq)	+ 3 PO43- (aq)	+ OH– (aq)
   			______	______	x

   Check Answer: ^[51]

2. Complete the changes in concentrations for each of the following reactions in the table below:
   

   a.	BaSO4 (s)	→	Ba2+ (aq)	+ SO42- (aq)
   			x	______
   b.	Ag2SO4 (s)	→	2 Ag+ (aq)	+ SO42- (aq)
   			______	x
   c.	Al(OH)3 (s)	→	Al3+ (aq)	+ 3 OH– (aq)
   			x	______
   d.	Pb(OH)Cl (s)	→	Pb2+ (aq)	+ OH– (aq)	+ Cl– (aq)
   			______	x	______
   e.	Ca3(AsO4)2 (s)	→	3 Ca2+ (aq)	+ 2 AsO43- (aq)
   			3x	______

3. How do the concentrations of Ag⁺ and CrO₄^2- in a saturated solution above 1.0 g of solid Ag₂CrO₄ change when 100 g of solid Ag₂CrO₄ is added to the system? Explain. Check Answer: ^[52]
4. How do the concentrations of Pb²⁺ and S^2– change when K₂S is added to a saturated solution of PbS?
5. What additional information do we need to answer the following question: How is the equilibrium of solid silver bromide with a saturated solution of its ions affected when the temperature is raised? Check Answer: ^[53]
6. Which of the following slightly soluble compounds has a solubility greater than that calculated from its solubility product because of hydrolysis of the anion present: CoSO₃, CuI, PbCO₃, PbCl₂, Tl₂S, KClO₄?
7. Which of the following slightly soluble compounds has a solubility greater than that calculated from its solubility product because of hydrolysis of the anion present: AgCl, BaSO₄, CaF₂, Hg₂I₂, MnCO₃, ZnS, PbS? Check Answer: ^[54]
8. Write the ionic equation for dissolution and the solubility product (K_sp) expression for each of the following slightly soluble ionic compounds:
   1. PbCl₂
   2. Ag₂S
   3. Sr₃(PO₄)₂
   4. SrSO₄
9. Write the ionic equation for the dissolution and the K_sp expression for each of the following slightly soluble ionic compounds:
   1. LaF₃
   2. CaCO₃
   3. Ag₂SO₄
   4. Pb(OH)₂
      Check Answer: ^[55]
10. The Handbook of Chemistry and Physics gives solubilities of the following compounds in grams per 100 mL of water. Because these compounds are only slightly soluble, assume that the volume does not change on dissolution and calculate the solubility product for each.
    1. BaSiF₆, 0.026 g/100 mL (contains SiF₆^2- ions)
    2. Ce(IO₃)₄, 1.5 × 10^–2 g/100 mL
    3. Gd₂(SO₄)₃, 3.98 g/100 mL
    4. (NH₄)₂PtBr₆, 0.59 g/100 mL (contains PtBr₆^2- ions)
11. The Handbook of Chemistry and Physics gives solubilities of the following compounds in grams per 100 mL of water. Because these compounds are only slightly soluble, assume that the volume does not change on dissolution and calculate the solubility product for each.
    1. BaSeO₄, 0.0118 g/100 mL
    2. Ba(BrO₃)₂·H₂O, 0.30 g/100 mL
    3. NH₄MgAsO₄·6H₂O, 0.038 g/100 mL
    4. La₂(MoO₄)₃, 0.00179 g/100 mL
       Check Answer: ^[56]
12. Use solubility products and predict which of the following salts is the most soluble, in terms of moles per litre, in pure water: CaF₂, Hg₂Cl₂, PbI₂, or Sn(OH)₂.
13. Assuming that no equilibria other than dissolution are involved, calculate the molar solubility of each of the following from its solubility product:
    1. KHC₄H₄O₆
    2. PbI₂
    3. Ag₄[Fe(CN)₆], a salt containing the Fe(CN)₄^– ion
    4. Hg₂I₂
       Check Answer: ^[57]
14. Assuming that no equilibria other than dissolution are involved, calculate the molar solubility of each of the following from its solubility product:
    1. Ag₂SO₄
    2. PbBr₂
    3. AgI
    4. CaC₂O₄·H₂O
15. Assuming that no equilibria other than dissolution are involved, calculate the concentration of all solute species in each of the following solutions of salts in contact with a solution containing a common ion. Show that changes in the initial concentrations of the common ions can be neglected.
    1. AgCl(s) in 0.025 M NaCl
    2. CaF₂(s) in 0.00133 M KF
    3. Ag₂SO₄(s) in 0.500 L of a solution containing 19.50 g of K₂SO₄
    4. Zn(OH)₂(s) in a solution buffered at a pH of 11.45
       Check Answer: ^[58]
16. Assuming that no equilibria other than dissolution are involved, calculate the concentration of all solute species in each of the following solutions of salts in contact with a solution containing a common ion. Show that changes in the initial concentrations of the common ions can be neglected.
    1. TlCl(s) in 1.250 M HCl
    2. PbI₂(s) in 0.0355 M CaI₂
    3. Ag₂CrO₄(s) in 0.225 L of a solution containing 0.856 g of K₂CrO₄
    4. Cd(OH)₂(s) in a solution buffered at a pH of 10.995
17. Assuming that no equilibria other than dissolution are involved, calculate the concentration of all solute species in each of the following solutions of salts in contact with a solution containing a common ion. Show that it is not appropriate to neglect the changes in the initial concentrations of the common ions.
    1. TlCl(s) in 0.025 M TlNO₃
    2. BaF₂(s) in 0.0313 M KF
    3. MgC₂O₄ in 2.250 L of a solution containing 8.156 g of Mg(NO₃)₂
    4. Ca(OH)₂(s) in an unbuffered solution initially with a pH of 12.700
       Check Answer: ^[59]
18. Calculate the solubility of aluminum hydroxide, Al(OH)₃, in a solution buffered at pH 11.00.
19. Refer to Appendix K for solubility products for calcium salts. Determine which of the calcium salts listed is most soluble in moles per litre and which is most soluble in grams per litre. Check Answer: ^[60]
20. Most barium compounds are very poisonous; however, barium sulfate is often administered internally as an aid in the X-ray examination of the lower intestinal tract (Figure 17.6c). This use of BaSO₄ is possible because of its low solubility. Calculate the molar solubility of BaSO₄ and the mass of barium present in 1.00 L of water saturated with BaSO₄.
21. Public Health Service standards for drinking water set a maximum of 250 mg/L (2.60 × 10^–3M) of SO₄^2- because of its cathartic action (it is a laxative). Does natural water that is saturated with CaSO₄ (“gyp” water) as a result or passing through soil containing gypsum, CaSO₄·2H₂O, meet these standards? What is SO₄^2- in such water? Check Answer: ^[61]
22. Perform the following calculations:
    1. Calculate [Ag⁺] in a saturated aqueous solution of AgBr.
    2. What will [Ag⁺] be when enough KBr has been added to make [Br^–] = 0.050 M?
    3. What will [Br^–] be when enough AgNO₃ has been added to make [Ag⁺] = 0.020 M?
23. The solubility product of CaSO₄·2H₂O is 2.4 × 10^–5. What mass of this salt will dissolve in 1.0 L of 0.010 M SO₄^2-? Check Answer: ^[62]
24. Assuming that no equilibria other than dissolution are involved, calculate the concentrations of ions in a saturated solution of each of the following (see Appendix K for solubility products).
    1. TlCl
    2. BaF₂
    3. Ag₂CrO₄
    4. CaC₂O₄·H₂O
    5. the mineral anglesite, PbSO₄
25. Assuming that no equilibria other than dissolution are involved, calculate the concentrations of ions in a saturated solution of each of the following (see Appendix K for solubility products):
    1. AgI
    2. Ag₂SO₄
    3. Mn(OH)₂
    4. Sr(OH)₂·8H₂O
    5. the mineral brucite, Mg(OH)₂
       Check Answer: ^[63]
26. The following concentrations are found in mixtures of ions in equilibrium with slightly soluble solids. From the concentrations given, calculate K_sp for each of the slightly soluble solids indicated:
    1. AgBr: [Ag⁺] = 5.7 × 10^–7M, [Br^–] = 5.7 × 10^–7M
    2. CaCO₃: [Ca²⁺] = 5.3 × 10^–3M, [CO₃^2-] = 9.0 × 10^–7M
    3. PbF₂: [Pb²⁺] = 2.1 × 10^–3M, [F^–] = 4.2 × 10^–3M
    4. Ag₂CrO₄: [Ag⁺] = 5.3 × 10^–5M, 3.2 × 10^–3M
    5. InF₃: [In³⁺] = 2.3 × 10^–3M, [F^–] = 7.0 × 10^–3M
27. The following concentrations are found in mixtures of ions in equilibrium with slightly soluble solids. From the concentrations given, calculate K_sp for each of the slightly soluble solids indicated:
    1. TlCl: [Tl⁺] = 1.21 × 10^–2M, [Cl^–] = 1.2 × 10^–2M
    2. Ce(IO₃)₄: [Ce⁴⁺] = 1.8 × 10^–4M, [IO₃^–] = 2.6 × 10^–13M
    3. Gd₂(SO₄)₃: [Gd³⁺] = 0.132 M, [SO₄^2-] = 0.198 M
    4. Ag₂SO₄: [Ag⁺] = 2.40 × 10^–2M, [SO₄^2-] = 2.05 × 10^–2M
    5. BaSO₄: [Ba²⁺] = 0.500 M, [SO₄^2-] = 2.16 × 10^–10M
       Check Answer: ^[64]
28. Which of the following compounds precipitates from a solution that has the concentrations indicated? (See Appendix K for K_sp values.)
    1. KClO₄: [K⁺] = 0.01 M, [ClO₄^–] = 0.01 M
    2. K₂PtCl₆: [K⁺] = 0.01 M, [PtCl₆^2-] = 0.01 M
    3. PbI₂: [Pb²⁺] = 0.003 M, [I^–] = 1.3 × 10^–3M
    4. Ag₂S: [Ag⁺] = 1 × 10^–10M, [S^2–] = 1 × 10^–13M
29. Which of the following compounds precipitates from a solution that has the concentrations indicated? (See Appendix K for K_sp values.)
    1. CaCO₃: [Ca²⁺] = 0.003 M, [CO₃^2-] = 0.003 M
    2. Co(OH)₂: [Co²⁺] = 0.01 M, [OH^–] = 1 × 10^–7M
    3. CaHPO₄: [Ca²⁺] = 0.01 M, [HPO₄^2-] = 2 × 10^–6M
    4. Pb₃(PO₄)₂: [Pb²⁺] = 0.01 M, [PO₄^3-] = 1 × 10^–13M
       Check Answer: ^[65]
30. Calculate the concentration of Tl⁺ when TlCl just begins to precipitate from a solution that is 0.0250 M in Cl^–.
31. Calculate the concentration of sulfate ion when BaSO₄ just begins to precipitate from a solution that is 0.0758 M in Ba²⁺. Check Answer: ^[66]
32. Calculate the concentration of Sr²⁺ when SrF₂ starts to precipitate from a solution that is 0.0025 M in F^–.
33. Calculate the concentration of PO₄^3- when Ag₃PO₄ starts to precipitate from a solution that is 0.0125 M in Ag⁺. Check Answer: ^[67]
34. Calculate the concentration of F^– required to begin precipitation of CaF₂ in a solution that is 0.010 M in Ca²⁺.
35. Calculate the concentration of Ag⁺ required to begin precipitation of Ag₂CO₃ in a solution that is 2.50 × 10^–6M in CO₃^2-. Check Answer: ^[68]
36. What [Ag⁺] is required to reduce [CO₃^2-] to 8.2 × 10^–4M by precipitation of Ag₂CO₃?
37. What [F^–] is required to reduce [Ca²⁺] to 1.0 × 10^–4M by precipitation of CaF₂? Check Answer: ^[69]
38. A volume of 0.800 L of a 2 × 10^–4–M Ba(NO₃)₂ solution is added to 0.200 L of 5 × 10^–4M Li₂SO₄. Does BaSO₄ precipitate? Explain your answer.
39. Perform these calculations for nickel(II) carbonate.
    1. With what volume of water must a precipitate containing NiCO₃ be washed to dissolve 0.100 g of this compound? Assume that the wash water becomes saturated with NiCO₃ (K_sp = 1.36 × 10^–7).
    2. If the NiCO₃ were a contaminant in a sample of CoCO₃ (K_sp = 1.0 × 10^–12), what mass of CoCO₃ would have been lost? Keep in mind that both NiCO₃ and CoCO₃ dissolve in the same solution.
       Check Answer: ^[70]
40. Iron concentrations greater than 5.4 × 10^–6M in water used for laundry purposes can cause staining. What [OH^–] is required to reduce [Fe²⁺] to this level by precipitation of Fe(OH)₂?
41. A solution is 0.010 M in both Cu²⁺ and Cd²⁺. What percentage of Cd²⁺ remains in the solution when 99.9% of the Cu²⁺ has been precipitated as CuS by adding sulfide? Check Answer: ^[71]
42. A solution is 0.15 M in both Pb²⁺ and Ag⁺. If Cl^– is added to this solution, what is [Ag⁺] when PbCl₂ begins to precipitate?
43. What reagent might be used to separate the ions in each of the following mixtures, which are 0.1 M with respect to each ion? In some cases it may be necessary to control the pH. (Hint: Consider the K_sp values given in Appendix K.)
    1. Hg₂²⁺ and Cu²⁺
    2. SO₄^2- and Cl^–
    3. Hg²⁺ and Co²⁺
    4. Zn²⁺ and Sr²⁺
    5. Ba²⁺ and Mg²⁺
    6. CO₃^2- and OH^–
       Check Answer: ^[72]
44. A solution contains 1.0 × 10^–5 mol of KBr and 0.10 mol of KCl per litre. AgNO₃ is gradually added to this solution. Which forms first, solid AgBr or solid AgCl?
45. A solution contains 1.0 × 10^–2 mol of KI and 0.10 mol of KCl per litre. AgNO₃ is gradually added to this solution. Which forms first, solid AgI or solid AgCl? Check Answer: ^[73]
46. The calcium ions in human blood serum are necessary for coagulation. Potassium oxalate, K₂C₂O₄, is used as an anticoagulant when a blood sample is drawn for laboratory tests because it removes the calcium as a precipitate of CaC₂O₄·H₂O. It is necessary to remove all but 1.0% of the Ca²⁺ in serum in order to prevent coagulation. If normal blood serum with a buffered pH of 7.40 contains 9.5 mg of Ca²⁺ per 100 mL of serum, what mass of K₂C₂O₄ is required to prevent the coagulation of a 10 mL blood sample that is 55% serum by volume? (All volumes are accurate to two significant figures. Note that the volume of serum in a 10-mL blood sample is 5.5 mL. Assume that the K_sp value for CaC₂O₄ in serum is the same as in water.)
47. About 50% of urinary calculi (kidney stones) consist of calcium phosphate, Ca₃(PO₄)₂. The normal mid range calcium content excreted in the urine is 0.10 g of Ca²⁺ per day. The normal mid range amount of urine passed may be taken as 1.4 L per day. What is the maximum concentration of phosphate ion that urine can contain before a calculus begins to form? Check Answer: ^[74]
48. The pH of normal urine is 6.30, and the total phosphate concentration [PO₄^3-] + [HPO₄^2-] + [H₂PO₄^–] + [H₃PO₄] is 0.020 M. What is the minimum concentration of Ca²⁺ necessary to induce kidney stone formation?
49. Magnesium metal (a component of alloys used in aircraft and a reducing agent used in the production of uranium, titanium, and other active metals) is isolated from sea water by the following sequence of reactions:
    [latex]\text{Mg}^{2+}(aq)\;+\;\text{Ca(OH)}_2(aq)\;{\longrightarrow}\;\text{Mg(OH)}_2(s)\;+\;\text{Ca}^{2+}(aq)[/latex]
    [latex]\text{Mg(OH)}_2(s)\;+\;2\text{HCl}(aq)\;{\longrightarrow}\;\text{MgCl}_2(s)\;+\;2\text{H}_2\text{O}(l)[/latex]
    [latex]\text{MgCl}_2(l)\;{\xrightarrow{\text{electrolysis}}}\;\text{Mg}(s)\;+\;\text{Cl}_2(g)[/latex]
    Sea water has a density of 1.026 g/cm³ and contains 1272 parts per million of magnesium as Mg²⁺(aq) by mass. What mass, in kilograms, of Ca(OH)₂ is required to precipitate 99.9% of the magnesium in 1.00 × 10³ L of sea water? Check Answer: ^[75]
50. Hydrogen sulfide is bubbled into a solution that is 0.10 M in both Pb²⁺ and Fe²⁺ and 0.30 M in HCl. After the solution has come to equilibrium it is saturated with H₂S ([H₂S] = 0.10 M). What concentrations of Pb²⁺ and Fe²⁺ remain in the solution? For a saturated solution of H₂S we can use the equilibrium:
    [latex]\text{H}_2\text{S}(aq)\;+\;2\text{H}_2\text{O}(l)\;{\leftrightharpoons}\;2\text{H}_3\text{O}^{+}(aq)\;+\;\text{S}^{2-}(aq)\;\;\;\;\;\;\;K = 1.0\;\times\;10^{-26}[/latex]

    (Hint: The [H₃O⁺] changes as metal sulfides precipitate.)

51. Perform the following calculations involving concentrations of iodate ions:
    1. The iodate ion concentration of a saturated solution of La(IO₃)₃ was found to be 3.1 × 10^–3 mol/L. Find the K_sp.
    2. Find the concentration of iodate ions in a saturated solution of Cu(IO₃)₂ (K_sp = 7.4 × 10^–8).
       Check Answer: ^[76]
52. Calculate the molar solubility of AgBr in 0.035 M NaBr (K_sp = 5 × 10^–13).
53. How many grams of Pb(OH)₂ will dissolve in 500 mL of a 0.050-M PbCl₂ solution (K_sp = 1.2 × 10^–15)?  Check Answer: ^[77]
54. How many grams of Milk of Magnesia, Mg(OH)₂ (s) (58.3 g/mol), would be soluble in 200 mL of water. K_sp = 7.1 × 10^–12. Include the ionic reaction and the expression for K_sp in your answer. (K_w = 1 × 10^–14 = [H₃O⁺][OH^–])
55. Two hypothetical salts, LM₂ and LQ, have the same molar solubility in H₂O. If K_sp for LM₂ is 3.20 × 10^–5, what is the K_sp value for LQ? Check Answer: ^[78]
56. Which of the following carbonates will form first? Which of the following will form last? Explain.
    1. [latex]\text{MgCO}_3\;\;\;\;\;\;\;K_{\text{sp}} = 3.5\;\times\;10^{-8}[/latex]
    2. [latex]\text{CaCO}_3\;\;\;\;\;\;\;K_{\text{sp}} = 4.2\;\times\;10^{-7}[/latex]
    3. [latex]\text{SrCO}_3\;\;\;\;\;\;\;K_{\text{sp}} = 3.9\;\times\;10^{-9}[/latex]
    4. [latex]\text{BaCO}_3\;\;\;\;\;\;\;K_{\text{sp}} = 4.4\;\times\;10^{-5}[/latex]
    5. [latex]\text{MnCO}_3\;\;\;\;\;\;\;K_{\text{sp}} = 5.1\;\times\;10^{-9}[/latex]
       Check Answer: ^[79]
57. How many grams of Zn(CN)₂(s) (117.44 g/mol) would be soluble in 100 mL of H₂O? Include the balanced reaction and the expression for K_sp in your answer. The K_sp value for Zn(CN)₂(s) is 3.0 × 10^–16.

17.7 Relative Strengths of Acids and Bases

1. Explain why the neutralization reaction of a strong acid and a weak base gives a weakly acidic solution.
2. Explain why the neutralization reaction of a weak acid and a strong base gives a weakly basic solution. Check Answer: ^[80]
3. Use this list of important industrial compounds (and Figure 17.7c) to answer the following questions regarding: CaO, Ca(OH)₂, CH₃CO₂H, CO_2, HCl, H₂CO₃, HF, HNO₂, HNO₃, H₃PO₄, H₂SO₄, NH₃, NaOH, Na₂CO₃.
   1. Identify the strong Brønsted-Lowry acids and strong Brønsted-Lowry bases.
   2. List those compounds in (a) that can behave as Brønsted-Lowry acids with strengths lying between those of H₃O⁺ and H₂O.
   3. List those compounds in (a) that can behave as Brønsted-Lowry bases with strengths lying between those of H₂O and OH⁻.
4. The odour of vinegar is due to the presence of acetic acid, CH₃CO₂H, a weak acid. List, in order of descending concentration, all of the ionic and molecular species present in a 1-M aqueous solution of this acid. Check Answer: ^[81]
5. Household ammonia is a solution of the weak base NH₃ in water. List, in order of descending concentration, all of the ionic and molecular species present in a 1-M aqueous solution of this base.
6. Explain why the ionization constant, K_a, for H₂SO₄ is larger than the ionization constant for H₂SO₃. Check Answer: ^[82]
7. Explain why the ionization constant, K_a, for HI is larger than the ionization constant for HF.
8. Gastric juice, the digestive fluid produced in the stomach, contains hydrochloric acid, HCl. Milk of Magnesia, a suspension of solid Mg(OH)₂ in an aqueous medium, is sometimes used to neutralize excess stomach acid. Write a complete balanced equation for the neutralization reaction, and identify the conjugate acid-base pairs. Check Answer: ^[83]
9. Nitric acid reacts with insoluble copper(II) oxide to form soluble copper(II) nitrate, Cu(NO₃)₂, a compound that has been used to prevent the growth of algae in swimming pools. Write the balanced chemical equation for the reaction of an aqueous solution of HNO₃ with CuO.
10. What is the ionization constant at 25 °C for the weak acid CH₃NH₃⁺, the conjugate acid of the weak base CH₃NH₂, K_b = 4.4 × 10⁻⁴. Check Answer: ^[84]
11. What is the ionization constant at 25 °C for the weak acid (CH₃)₂NH₂⁺, the conjugate acid of the weak base (CH₃)₂NH, K_b = 5.9 × 10⁻⁴?
12. Which base, CH₃NH₂ or (CH₃)₂NH, is the stronger base? Which conjugate acid, (CH₃)₂NH₂⁺ or (CH₃)₂NH, is the stronger acid? Check Answer: ^[85]
13. Which is the stronger acid, NH₄⁺ or HBrO?
14. Which is the stronger base, (CH₃)₃N or H₂BO₃^–? Check Answer: ^[86]
15. Predict which acid in each of the following pairs is the stronger and explain your reasoning for each.
    1. H₂O or HF
    2. B(OH)₃ or Al(OH)₃
    3. HSO₃^– or HSO₄^–
    4. NH₃ or H₂S
    5. H₂O or H₂Te
16. Predict which compound in each of the following pairs of compounds is more acidic and explain your reasoning for each.
    1. HSO₄^– or HSeO₄^–
    2. NH₃ or H₂O
    3. PH₃ or HI
    4. NH₃ or PH₃
    5. H₂S or HBr
       Check Answer: ^[87]
17. Rank the compounds in each of the following groups in order of increasing acidity or basicity, as indicated, and explain the order you assign.
    1. acidity: HCl, HBr, HI
    2. basicity: H₂O, OH⁻, H⁻, Cl⁻
    3. basicity: Mg(OH)₂, Si(OH)₄, ClO₃(OH) (Hint: Formula could also be written as HClO₄).
    4. acidity: HF, H₂O, NH₃, CH₄
18. Rank the compounds in each of the following groups in order of increasing acidity or basicity, as indicated, and explain the order you assign.
    1. acidity: NaHSO₃, NaHSeO₃, NaHSO₄
    2. basicity: BrO₂^–, ClO₂^–, IO₂^–
    3. acidity: HOCl, HOBr, HOI
    4. acidity: HOCl, HOClO, HOClO₂, HOClO₃
    5. basicity: NH₂^–, HS⁻, HTe⁻, PH₂^–
    6. basicity: BrO⁻, BrO₂^–, BrO₃^–, BrO₄^–
       Check Answer: ^[88]</li>
19. Both HF and HCN ionize in water to a limited extent. Which of the conjugate bases, F⁻ or CN⁻, is the stronger base? See Table 17.7b.
20. The active ingredient formed by aspirin in the body is salicylic acid, C₆H₄OH(CO₂H). The carboxyl group (−CO₂H) acts as a weak acid. The phenol group (an OH group bonded to an aromatic ring) also acts as an acid but a much weaker acid. List, in order of descending concentration, all of the ionic and molecular species present in a 0.001-M aqueous solution of C₆H₄OH(CO₂H). Check Answer: ^[89]
21. What do we represent when we write:
    [latex]\text{CH}_3\text{CO}_2\text{H}(aq)\;+\;\text{H}_2\text{O}(l)\;{\rightleftharpoons}\;\text{H}_3\text{O}^{+}(aq)\;+\;\text{CH}_3\text{CO}_2^{\;\;-}(aq)[/latex]?
22. Explain why equilibrium calculations are not necessary to determine ionic concentrations in solutions of certain strong electrolytes such as NaOH and HCl. Under what conditions are equilibrium calculations necessary as part of the determination of the concentrations of all ions of some other strong electrolytes in solution? Check Answer: ^[90]
23. Are the concentrations of hydronium ion and hydroxide ion in a solution of an acid or a base in water directly proportional or inversely proportional? Explain your answer.
24. What two common assumptions can simplify calculation of equilibrium concentrations in a solution of a weak acid? Check Answer: ^[91]
25. What two common assumptions can simplify calculation of equilibrium concentrations in a solution of a weak base?
26. Which of the following will increase the percent of NH₃ that is converted to the ammonium ion in water (Hint: Use LeChâtelier’s principle.)?
    1. addition of NaOH
    2. addition of HCl
    3. addition of NH₄Cl
       Check Answer: ^[92]
27. Which of the following will increase the percent of HF that is converted to the fluoride ion in water?
    1. addition of NaOH
    2. addition of HCl
    3. addition of NaF
28. What is the effect on the concentrations of NO₂⁻, HNO₂, and OH⁻ when the following are added to a solution of KNO₂ in water:
    1. HCl
    2. HNO₂
    3. NaOH
    4. NaCl
    5. KNO
       The equation for the equilibrium is:[latex]\text{NO}_2^{\;\;-}(aq)\;+\;\text{H}_2\text{O}(l)\;{\rightleftharpoons}\;\text{HNO}_2(aq)\;+\;\text{OH}^{-}(aq)[/latex]
       Check Answer: ^[93]
29. What is the effect on the concentration of hydrofluoric acid, hydronium ion, and fluoride ion when the following are added to separate solutions of hydrofluoric acid?
    1. HCl
    2. KF
    3. NaCl
    4. KOH
    5. HF
       The equation for the equilibrium is:[latex]\text{HF}(aq)\;+\;\text{H}_2\text{O}(l)\;{\rightleftharpoons}\;\text{H}_3\text{O}^{+}(aq)\;+\;\text{F}^{-}(aq)[/latex]
30. Why is the hydronium ion concentration in a solution that is 0.10 M in HCl and 0.10 M in HCOOH determined by the concentration of HCl? Check Answer: ^[94]
31. From the equilibrium concentrations given, calculate K_a for each of the weak acids and K_b for each of the weak bases.
    1. CH₃CO₂H: [H₃O⁺] = 1.34 × 10⁻³M;
       [CH₃CO₂^-] = 1.34 × 10⁻³M;
       [CH₃CO₂H] = 9.866 × 10⁻²M;

    2. ClO⁻: [OH⁻] = 4.0 × 10⁻⁴M;
       [HClO] = 2.38 × 10⁻⁵M;
       [ClO⁻] = 0.273 M;

    3. HCO₂H: [HCO₂H] = 0.524 M;
       [H₃O⁺] = 9.8 × 10⁻³M;
       [HCO₂^-] = 9.8 × 10⁻³M;

    4. C₆H₅NH₃⁺: [C₆H₅NH₃⁺] = 0.233 M;
       [C₆H₅NH₂] = 2.3 × 10⁻³M;
       [H₃O⁺] = 2.3 × 10⁻³M

32. From the equilibrium concentrations given, calculate K_a for each of the weak acids and K_b for each of the weak bases.
    1. NH₃: [OH⁻] = 3.1 × 10⁻³M;
       [NH₄⁺] = 3.1 × 10⁻³M;
       [NH₃] = 0.533 M;

    2. HNO₂: [H₃O⁺] = 0.011 M;
       [NO₂^-] = 0.0438 M;
       [HNO₂] = 1.07 M;

    3. (CH₃)₃N: [(CH₃)₃N] = 0.25 M;
       [(CH₃)₃NH⁺] = 4.3 × 10⁻³M;
       [OH⁻] = 4.3 × 10⁻³M;

    4. NH₄⁺: [NH₄⁺] = 0.100 M;
       [NH₃] = 7.5 × 10⁻⁶M;
       [H₃O⁺] = 7.5 × 10⁻⁶M
       Check Answer: ^[95]

33. Determine K_b for the nitrite ion, NO₂^-. In a 0.10-M solution this base is 0.0015% ionized.
34. Determine K_a for hydrogen sulfate ion, HSO₄^-. In a 0.10-M solution the acid is 29% ionized. Check Answer: ^[96]
35. Calculate the ionization constant for each of the following acids or bases from the ionization constant of its conjugate base or conjugate acid:
    1. [latex]\text{F}^{-}[/latex]
    2. [latex]\text{NH}_4^{\;+}[/latex]
    3. [latex]\text{AsO}_4^{\;3-}[/latex]
    4. [latex](\text{CH}_3)_2\text{NH}_2^{\;+}[/latex]
    5. [latex]\text{NO}_2^{\;-}[/latex]
    6. [latex]\text{HC}_2\text{O}_4^{\;-}[/latex] (as a base)
36. Calculate the ionization constant for each of the following acids or bases from the ionization constant of its conjugate base or conjugate acid:
    1. [latex]\text{HTe}^{-}[/latex] (as a base)
    2. [latex](\text{CH}_3)_3\text{NH}^{+}[/latex]
    3. [latex]\text{HAsO}_4^{\;3-}[/latex] (as a base)
    4. [latex]\text{HO}_2^{\;-}[/latex] (as a base)
    5. [latex]\text{C}_6\text{H}_5\text{NH}_3^{\;+}[/latex]
    6. [latex]\text{HSO}_3^{\;-}[/latex] (as a base)
       Check Answer: ^[97]
37. For which of the following solutions must we consider the ionization of water when calculating the pH or pOH?
    1. 3 × 10⁻⁸M HNO₃
    2. 0.10 g HCl in 1.0 L of solution
    3. 0.00080 g NaOH in 0.50 L of solution
    4. 1 × 10⁻⁷M Ca(OH)₂
    5. 0.0245 M KNO₃
38. Even though both NH₃ and C₆H₅NH₂ are weak bases, NH₃ is a much stronger acid than C₆H₅NH₂. Which of the following is correct at equilibrium for a solution that is initially 0.10 M in NH₃ and 0.10 M in C₆H₅NH₂?
    1. [latex][\text{OH}^{-}] = [\text{NH}_4^{\;+}][/latex]
    2. [latex][\text{NH}_4^{\;+}] = [\text{C}_6\text{H}_5\text{NH}_3^{\;+}][/latex]
    3. [latex][\text{OH}^{-}] = [\text{C}_6\text{H}_5\text{NH}_3^{\;+}][/latex]
    4. [latex][\text{NH}_3] = [\text{C}_6\text{H}_5\text{NH}_2][/latex]
    5. both a and b are correct
       Check Answer: ^[98]
39. Calculate the equilibrium concentration of the nonionized acids and all ions in a solution that is 0.25 M in HCO₂H and 0.10 M in HClO.
40. Calculate the equilibrium concentration of the nonionized acids and all ions in a solution that is 0.134 M in HNO₂ and 0.120 M in HBrO. Check Answer: ^[99]
41. Calculate the equilibrium concentration of the nonionized bases and all ions in a solution that is 0.25 M in CH₃NH₂ and 0.10 M in C₅H₅N (K_b = 1.7 × 10⁻⁹).
42. Calculate the equilibrium concentration of the nonionized bases and all ions in a solution that is 0.115 M in NH₃ and 0.100 M in C₆H₅NH₂. Check Answer: ^[100]
43. Using the K_a value of 1.4 × 10⁻⁵, place Al(H₂O)₆³⁺ in the correct location in Figure 17.7c.
44. Calculate the concentration of all solute species in each of the following solutions of acids or bases. Assume that the ionization of water can be neglected, and show that the change in the initial concentrations can be neglected. Ionization constants can be found in Appendix I and Appendix J.
    1. 0.0092 M HClO, a weak acid
    2. 0.0784 M C₆H₅NH₂, a weak base
    3. 0.0810 M HCN, a weak acid
    4. 0.11 M (CH₃)₃N, a weak base
    5. 0.120 M FeH₂O₆²⁺ a weak acid, K_a = 1.6 × 10⁻⁷
       Check Answer: ^[101]
45. Propionic acid, C₂H₅CO₂H (K_a = 1.34 × 10⁻⁵), is used in the manufacture of calcium propionate, a food preservative. What is the hydronium ion concentration in a 0.698-M solution of C₂H₅CO₂H?
46. White vinegar is a 5.0% by mass solution of acetic acid in water. If the density of white vinegar is 1.007 g/cm³, what is the pH? Check Answer: ^[102]
47. The ionization constant of lactic acid, CH₃CH(OH)CO₂H, an acid found in the blood after strenuous exercise, is 1.36 × 10⁻⁴. If 20.0 g of lactic acid is used to make a solution with a volume of 1.00 L, what is the concentration of hydronium ion in the solution?
48. Nicotine, C₁₀H₁₄N₂, is a base that will accept two protons (K₁ = 7 × 10⁻⁷, K₂ = 1.4 × 10⁻¹¹). What is the concentration of each species present in a 0.050-M solution of nicotine? Check Answer: ^[103]
49. The pH of a 0.20-M solution of HF is 1.92. Determine K_a for HF from these data.
50. The pH of a 0.15-M solution of HSO₄^- is 1.43. Determine K_a for HSO₄^- from these data. Check Answer: ^[104]
51. The pH of a 0.10-M solution of caffeine is 11.16. Determine K_b for caffeine from these data:
    [latex]\text{C}_8\text{H}_{10}\text{N}_4\text{O}_2(aq)\;+\;\text{H}_2\text{O}(l)\;{\leftrightharpoons}\;\text{C}_8\text{H}_{10}\text{N}_4\text{O}_2\text{H}^{+}(aq)\;+\;\text{OH}^{-}(aq)[/latex]
52. The pH of a solution of household ammonia, a 0.950 M solution of NH_3, is 11.612. Determine K_b for NH₃ from these data. Check Answer: ^[105]

17.8 Real World Examples of Equilibria

1. A saturated solution of a slightly soluble electrolyte in contact with some of the solid electrolyte is said to be a system in equilibrium. Explain. Why is such a system called a heterogeneous equilibrium?
2. Calculate the equilibrium concentration of Ni²⁺ in a 1.0-M solution [Ni(NH₃)₆](NO₃)₂. Check Answer: ^[106]
3. Calculate the equilibrium concentration of Zn²⁺ in a 0.30-M solution of Zn(CN)₄^2-.
4. Calculate the equilibrium concentration of Cu²⁺ in a solution initially with 0.050 M Cu²⁺ and 1.00 M NH₃. Check Answer: ^[107]
5. Calculate the equilibrium concentration of Zn²⁺ in a solution initially with 0.150 M Zn²⁺ and 2.50 M CN^–.
6. Calculate the Fe³⁺ equilibrium concentration when 0.0888 mole of K₃[Fe(CN)₆] is added to a solution with 0.0.00010 M CN^–. Check Answer: ^[108]
7. Calculate the Co²⁺ equilibrium concentration when 0.100 mole of [Co(NH₃)₆](NO₃)₂ is added to a solution with 0.025 M NH₃. Assume the volume is 1.00 L.
8. The equilibrium constant for the reaction [latex]\text{Hg}^{2+}(aq)\;+\;2\text{Cl}^{-}(aq)\;{\leftrightharpoons}\;\text{HgCl}_2(aq)[/latex] is 1.6 × 10¹³. Is HgCl₂ a strong electrolyte or a weak electrolyte? What are the concentrations of Hg²⁺ and Cl^– in a 0.015-M solution of HgCl₂? Check Answer: ^[109]
9. Calculate the molar solubility of Sn(OH)₂ in a buffer solution containing equal concentrations of NH₃ and NH₄⁺.
10. Calculate the molar solubility of Al(OH)₃ in a buffer solution with 0.100 M NH₃ and 0.400 M NH₄⁺. Check Answer: ^[110]
11. What is the molar solubility of CaF₂ in a 0.100-M solution of HF? K_a for HF = 7.2 × 10^–4.
12. What is the molar solubility of BaSO₄ in a 0.250-M solution of NaHSO₄? K_a for HSO₄^- = 1.2 × 10^–2. Check Answer: ^[111]
13. What is the molar solubility of Tl(OH)₃ in a 0.10-M solution of NH₃?
14. What is the molar solubility of Pb(OH)₂ in a 0.138-M solution of CH₃NH₂? Check Answer: ^[112]
15. A solution of 0.075 M CoBr₂ is saturated with H₂S ([H₂S] = 0.10 M). What is the minimum pH at which CoS begins to precipitate?
    [latex]\text{CoS}(s)\;{\leftrightharpoons}\;\text{Co}^{2+}(aq)\;+\;\text{S}^{2-}(aq)\;\;\;\;\;\;\;K_{\text{sp}} = 4.5\;\times\;10^{-27}[/latex]
    [latex]\text{H}_2\text{S}(aq)\;+\;2\text{H}_2\text{O}(l)\;{\leftrightharpoons}\;2\text{H}_3\text{O}^{+}(aq)\;+\;\text{S}^{2-}(aq)\;\;\;\;\;\;\;K = 1.0\;\times\;10^{-26}[/latex]
16. A 0.125-M solution of Mn(NO₃)₂ is saturated with H₂S ([H₂S] = 0.10 M). At what pH does MnS begin to precipitate?
    [latex]\text{MnS}(s)\;{\rightleftharpoons}\;\text{Mn}^{2+}(aq)\;+\;\text{S}^{2-}(aq)\;\;\;\;\;\;\;K_{\text{sp}} = 4.3\;\times\;10^{-22}[/latex]
    [latex]\text{H}_2\text{S}(aq)\;+\;2\text{H}_2\text{O}(l)\;{\rightleftharpoons}\;2\text{H}_3\text{O}^{+}(aq)\;+\;\text{S}^{2-}(aq)\;\;\;\;\;\;\;K = 1.0\;\times\;10^{-26}[/latex]
    Check Answer: ^[113]
17. Calculate the molar solubility of BaF₂ in a buffer solution containing 0.20 M HF and 0.20 M NaF.
18. Calculate the molar solubility of CdCO₃ in a buffer solution containing 0.115 M Na₂CO₃ and 0.120 M NaHCO₃ Check Answer: ^[114]
19. To a 0.10-M solution of Pb(NO₃)₂ is added enough HF(g) to make [HF] = 0.10 M.
    1. Does PbF₂ precipitate from this solution? Show the calculations that support your conclusion.
    2. What is the minimum pH at which PbF₂ precipitates?
20. Calculate the concentration of Cd²⁺ resulting from the dissolution of CdCO₃ in a solution that is 0.010 M in H₂CO₃. Check Answer: ^[115]
21. Both AgCl and AgI dissolve in NH₃.
    1. What mass of AgI dissolves in 1.0 L of 1.0 M NH₃?
    2. What mass of AgCl dissolves in 1.0 L of 1.0 M NH₃?
22. Calculate the volume of 1.50 M CH₃CO₂H required to dissolve a precipitate composed of 350 mg each of CaCO₃, SrCO₃, and BaCO₃. Check Answer: ^[116]
23. Even though Ca(OH)₂ is an inexpensive base, its limited solubility restricts its use. What is the pH of a saturated solution of Ca(OH)₂?
24. What mass of NaCN must be added to 1 L of 0.010 M Mg(NO₃)₂ in order to produce the first trace of Mg(OH)₂? Check Answer: ^[117]
25. Magnesium hydroxide and magnesium citrate function as mild laxatives when they reach the small intestine. Why do magnesium hydroxide and magnesium citrate, two very different substances, have the same effect in your small intestine. (Hint: The contents of the small intestine are basic.)
26. The following question is taken from a Chemistry Advanced Placement Examination and is used with the permission of the Educational Testing Service.
    Solve the following problem:
    [latex]\text{MgF}_2(s)\;{\rightleftharpoons}\;\text{Mg}^{2+}(aq)\;+\;2\text{F}^{-}(aq)[/latex]

    In a saturated solution of MgF₂ at 18 °C, the concentration of Mg²⁺ is 1.21 × 10^–3M. The equilibrium is represented by the preceding equation.

    1. Write the expression for the solubility-product constant, K_sp, and calculate its value at 18 °C.
    2. Calculate the equilibrium concentration of Mg²⁺ in 1.000 L of saturated MgF₂ solution at 18 °C to which 0.100 mol of solid KF has been added. The KF dissolves completely. Assume the volume change is negligible.
    3. Predict whether a precipitate of MgF₂ will form when 100.0 mL of a 3.00 × 10^–3-M solution of Mg(NO₃)₂ is mixed with 200.0 mL of a 2.00 × 10^–3-M solution of NaF at 18 °C. Show the calculations to support your prediction.
    4. At 27 °C the concentration of Mg²⁺ in a saturated solution of MgF₂ is 1.17 × 10^–3M. Is the dissolving of MgF₂ in water an endothermic or an exothermic process? Give an explanation to support your conclusion.
       Check Answer: ^[118]
27. Which of the following compounds, when dissolved in a 0.01-M solution of HClO₄, has a solubility greater than in pure water: CuCl, CaCO₃, MnS, PbBr₂, CaF₂? Explain your answer.
28. Which of the following compounds, when dissolved in a 0.01-M solution of HClO₄, has a solubility greater than in pure water: AgBr, BaF₂, Ca₃(PO₄)₃, ZnS, PbI₂? Explain your answer. Check Answer: ^[119]
29. What is the effect on the amount of solid Mg(OH)₂ that dissolves and the concentrations of Mg²⁺ and OH^– when each of the following are added to a mixture of solid Mg(OH)₂ and water at equilibrium?
    1. MgCl₂
    2. KOH
    3. HClO₄
    4. NaNO₃
    5. Mg(OH)₂
30. What is the effect on the amount of CaHPO₄ that dissolves and the concentrations of Ca²⁺ and HPO₄^- when each of the following are added to a mixture of solid CaHPO₄ and water at equilibrium?
    1. CaCl₂
    2. HCl
    3. KClO₄
    4. NaOH
    5. CaHPO₄
       Check Answer: ^[120]
31. Identify all chemical species present in an aqueous solution of Ca₃(PO₄)₂ and list these species in decreasing order of their concentrations. (Hint: Remember that the PO₄^3- ion is a weak base.)
32. A volume of 50 mL of 1.8 M NH₃ is mixed with an equal volume of a solution containing 0.95 g of MgCl₂. What mass of NH₄Cl must be added to the resulting solution to prevent the precipitation of Mg(OH)₂? Check Answer: ^[121]

Attribution & References