10.6 Atomic Properties and Periodic Table Trends
Learning Objectives
By the end of this section, you will be able to:
- Describe and explain the observed trends in atomic size, ionization energy, and electron affinity of the elements.
The elements in groups (vertical columns) of the periodic table exhibit similar chemical behaviour. This similarity occurs because the members of a group have the same number and distribution of electrons in their valence shells. However, there are also other patterns in chemical properties on the periodic table. For example, as we move down a group, the metallic character of the atoms increases. Oxygen, at the top of group 16 (6A), is a colourless gas; in the middle of the group, selenium is a semiconducting solid; and, toward the bottom, polonium is a silver-grey solid that conducts electricity.
As we go across a period from left to right, we add a proton to the nucleus and an electron to the valence shell with each successive element. As we go down the elements in a group, the number of electrons in the valence shell remains constant, but the principal quantum number increases by one each time. An understanding of the electronic structure of the elements allows us to examine some of the properties that govern their chemical behaviour. These properties vary periodically as the electronic structure of the elements changes. They are (1) size (radius) of atoms and ions, (2) ionization energies, and (3) electron affinities.
Variation in Covalent Radius
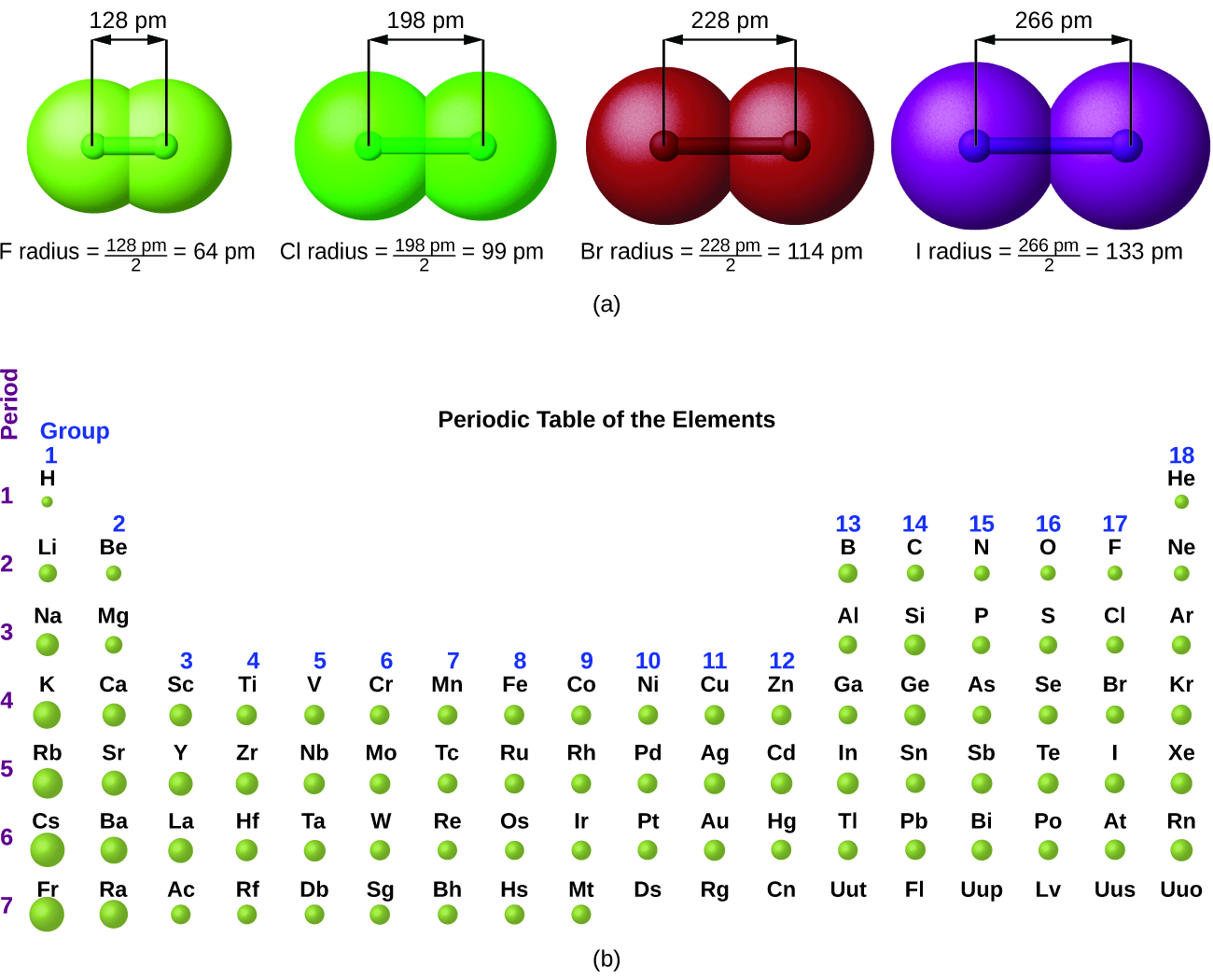
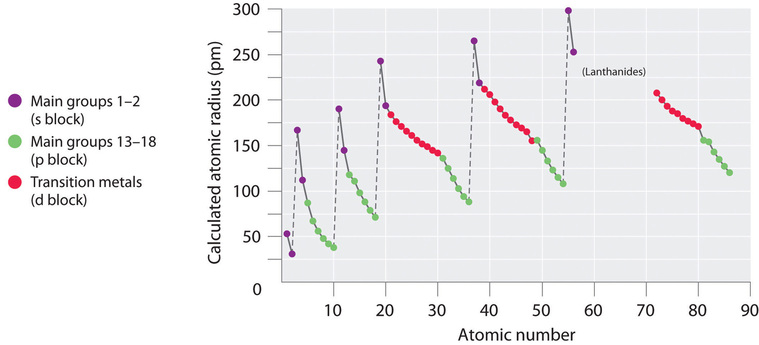
The quantum mechanical picture makes it difficult to establish a definite size of an atom. However, there are several practical ways to define the radius of atoms and, thus, to determine their relative sizes that give roughly similar values. We will use the covalent radius (Figure 10.6a), which is defined as one-half the distance between the nuclei of two identical atoms when they are joined by a covalent bond (this measurement is possible because atoms within molecules still retain much of their atomic identity). We know that as we scan down a group, the principal quantum number, n, increases by one for each element. Thus, the electrons are being added to a region of space that is increasingly distant from the nucleus. Consequently, the size of the atom (and its covalent radius) must increase as we increase the distance of the outermost electrons from the nucleus. This trend is illustrated for the covalent radii of the halogens in Table 10.6a and Figure 10.6a (a). The trends for the entire periodic table can be seen in Figure 10.6a (b).
| Atom | Covalent radius (pm) | Nuclear charge |
|---|---|---|
| F | 64 | +9 |
| Cl | 99 | +17 |
| Br | 114 | +35 |
| I | 133 | +53 |
| At | 148 | +85 |
As shown in Figure 10.6b, we see the general trend for atomic radii:
This might seem counterintuitive because it implies that atoms with more electrons have a smaller atomic radius. This can be explained with the concept of effective nuclear charge, Zeff. This is the pull exerted on a specific electron by the nucleus, taking into account any electron-electron repulsions. For hydrogen, there is only one electron and so the nuclear charge (Z) and the effective nuclear charge (Zeff) are equal. For all other atoms, the inner electrons partially shield the outer electrons from the pull of the nucleus, and thus:
[latex]Z_{\text{eff}} = Z - shielding[/latex]
Shielding is determined by the probability of another electron being between the electron of interest and the nucleus, as well as by the electron-electron repulsions the electron of interest encounters. Core electrons are adept at shielding, while electrons in the same valence shell do not block the nuclear attraction experienced by each other as efficiently. Thus, each time we move from one element to the next across a period, Z increases by one, but the shielding increases only slightly. Thus, Zeff increases as we move from left to right across a period. The stronger pull (higher effective nuclear charge) experienced by electrons on the right side of the periodic table draws them closer to the nucleus, making the covalent radii smaller.
Thus, as we would expect, the outermost or valence electrons are easiest to remove because they have the highest energies, are shielded more, and are farthest from the nucleus. As a general rule, when the representative elements form cations, they do so by the loss of the ns or np electrons that were added last in the Aufbau process. The transition elements, on the other hand, lose the ns electrons before they begin to lose the (n – 1)d electrons, even though the ns electrons are added first, according to the Aufbau principle.
Example 10.6a
Sorting Atomic Radii using Periodic Table Trends
Predict the order of increasing covalent radius for Ge, Pb, Br, Kr.
Solution
Order of increasing covalent radius means ordering elements in order of smallest to largest Radii. Here, the radius increases as we move down a group, so Ge < Pb. Radius decreases as we move across a period, so Kr < Br < Ge. Putting the trends together, we obtain Kr < Br < Ge < Pb.
Exercise 10.6a
- Give an example of an atom in group 2 whose size is larger than boron (B).
- Predict the order of decreasing covalent radius for Mg, Fr, Cs, Na, Ca
Check Your Answer[1]
Variation in Ionic Radii
Ionic radius is the measure used to describe the size of an ion. A cation always has fewer electrons and the same number of protons as the parent atom; it is smaller than the atom from which it is derived (Figure 10.6c). For example, the covalent radius of an aluminum atom (1s22s22p63s23p1) is 118 pm, whereas the ionic radius of an Al3+ (1s22s22p6) is 68 pm. As electrons are removed from the outer valence shell, the remaining core electrons occupying smaller shells experience a greater effective nuclear charge Zeff (as discussed) and are drawn even closer to the nucleus and the cation is smaller than the parent atom.

Cations with larger charges are smaller than cations with smaller charges (e.g., V2+ has an ionic radius of 79 pm, while that of V3+ is 64 pm). Proceeding down the groups of the periodic table, we find that cations of successive elements with the same charge generally have larger radii, corresponding to an increase in the principal quantum number, n.
An anion (negative ion) is formed by the addition of one or more electrons to the valence shell of an atom. This results in a greater repulsion among the electrons and a decrease in Zeff per electron. Both effects (the increased number of electrons and the decreased Zeff) cause the radius of an anion to be larger than that of the parent atom (Figure 10.6c). For example, a sulfur atom ([Ne]3s23p4) has a covalent radius of 104 pm; whereas, the ionic radius of the sulfide anion ([Ne]3s23p6) is 170 pm. For consecutive elements proceeding down any group, anions have larger principal quantum numbers and, thus, larger radii.
Atoms and ions that have the same electron configuration are said to be isoelectronic. Examples of isoelectronic species are N3–, O2–, F–, Ne, Na+, Mg2+, and Al3+, which all have an electron configuration 1s22s22p6. Another isoelectronic series is P3–, S2–, Cl–, Ar, K+, Ca2+, and Sc3+, which all have an electron configuration([Ne]3s23p6). For atoms or ions that are isoelectronic, the number of protons determines the size. The greater the nuclear charge, the smaller the radius in a series of isoelectronic ions and atoms.
Example 10.6b
Sorting Ionic Radii and Parent Atoms using Periodic Table Trends
Predict the order of increasing radius when comparing the following ions and parent atoms:
- Mg2+ and Mg
- N3- and N
- I- and I
- Cs+ and Cs
Solution
Cations have smaller atomic radii than their parent atom; whereas, anions have larger atomic radii than their parent atom. We were asked to order by increasing radii, so smaller radii followed by larger radius.
- Mg > Mg2+
- N3- > N
- I- > I
- Cs > Cs+
Example 10.6c
Sorting Ionic Radii and Parent Atoms using Periodic Table Trends
Predict the order of decreasing atomic radius when comparing the following ions/atoms:
- K+, Ba2+, F-, K, Ba, F
- Se2-, Br-, Kr, Rb+, Sr2+
Solution
Cations have smaller atomic radii than their parent atom; whereas, anions have larger atomic radii than their parent atom. We were asked to order by decreasing radii, so in order of largest radius to smallest radius.
- Ba > Ba2+ > K > K+ > F- > F
- These ions all have the same electron configuration [Ar]4s23d104p6 (the configuration of the noble gas Kr, [Kr]), and are said to be isoelectronic. For atoms or ions that are isoelectronic, the number of protons determines the size. The greater the nuclear charge (# of protons), the smaller the radius in a series of isoelectronic ions and atoms. Therefore, largest to smallest we have: Se2- > Br- > Kr > Rb+ > Sr2+
Exercise 10.6b
Predict the order of increasing atomic radius when comparing the following ions / atoms:
- K+, Cs2+, O2-, K, Fr, F-
- F-, O2-, Ne, Al3+, Mg2+
Check Your Answer[2]
Variation in Ionization Energies
The amount of energy required to remove the most loosely bound electron from a gaseous atom in its ground state is called its first ionization energy (IE1). The first ionization energy for an element, X, is the energy required to form a cation with +1 charge:
[latex]\text{X}(g) \longrightarrow \text{X}^+(g) + \text{e}^{-} \;\;\;\;\; \text{IE}_1[/latex]
The energy required to remove the second most loosely bound electron is called the second ionization energy (IE2).
[latex]\text{X}^+ (g) \longrightarrow \text{X}^{2+}(g) + \text{e}^{-} \;\;\;\;\; \text{IE}_2[/latex]
The energy required to remove the third electron is the third ionization energy, and so on. Energy is always required to remove electrons from atoms or ions, so ionization processes are endothermic and IE values are always positive. For larger atoms, the most loosely bound electron is located farther from the nucleus and so is easier to remove.
Relating this logic to what we have just learned about radii, we would expect first ionization energies to decrease down a group and to increase across a period. Generally speaking, atomic radius and ionization energy are inversely proportional to one another.
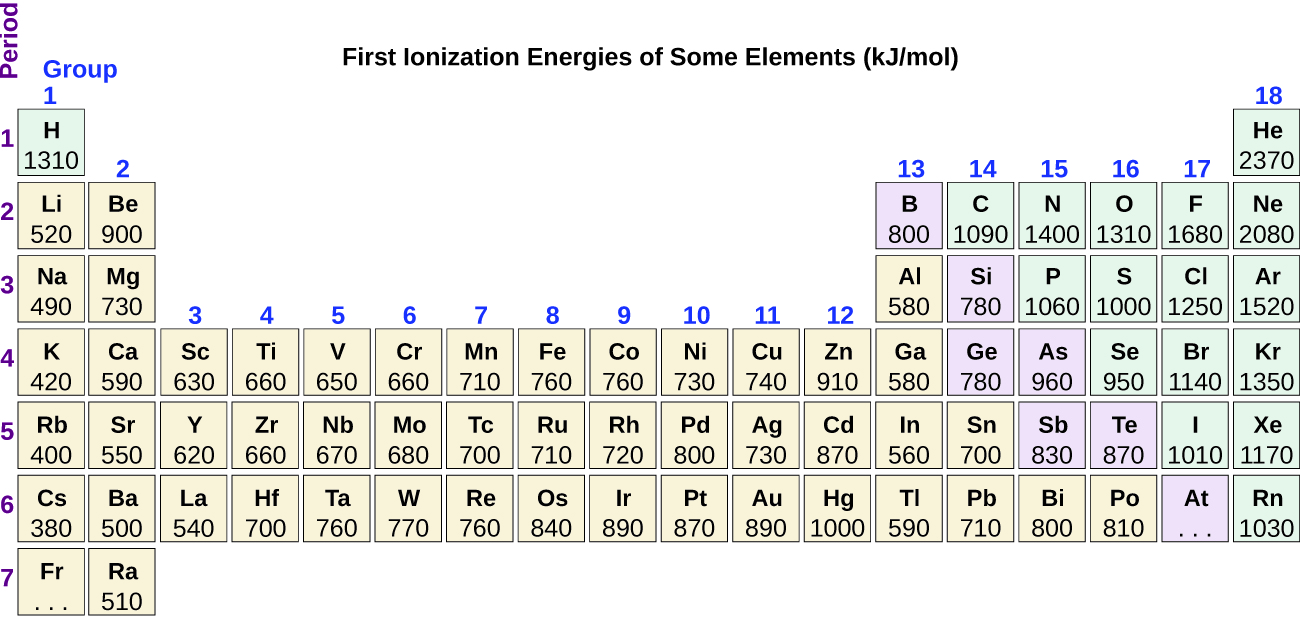
Figure 10.6d graphs the relationship between the first ionization energy and the atomic number of several elements. The values of first ionization energy for the elements are given in Figure 10.6d. Within a period, the IE1 generally increases with increasing Z. Down a group, the IE1 value generally decreases with increasing Z. There are some systematic deviations from this trend, however. Note that the ionization energy of boron (atomic number 5) is less than that of beryllium (atomic number 4) even though the nuclear charge of boron is greater by one proton. This can be explained because the energy of the subshells increases as l increases, due to penetration and shielding (as discussed previously). Within any one shell, the s electrons are lower in energy than the p electrons. This means that an s electron is harder to remove from an atom than a p electron in the same shell. The electron removed during the ionization of beryllium ([He]2s2) is an s electron, whereas the electron removed during the ionization of boron ([He]2s22p1) is a p electron; this results in a lower first ionization energy for boron, even though its nuclear charge is greater by one proton. Thus, we see a small deviation from the predicted trend occurring each time a new subshell begins.
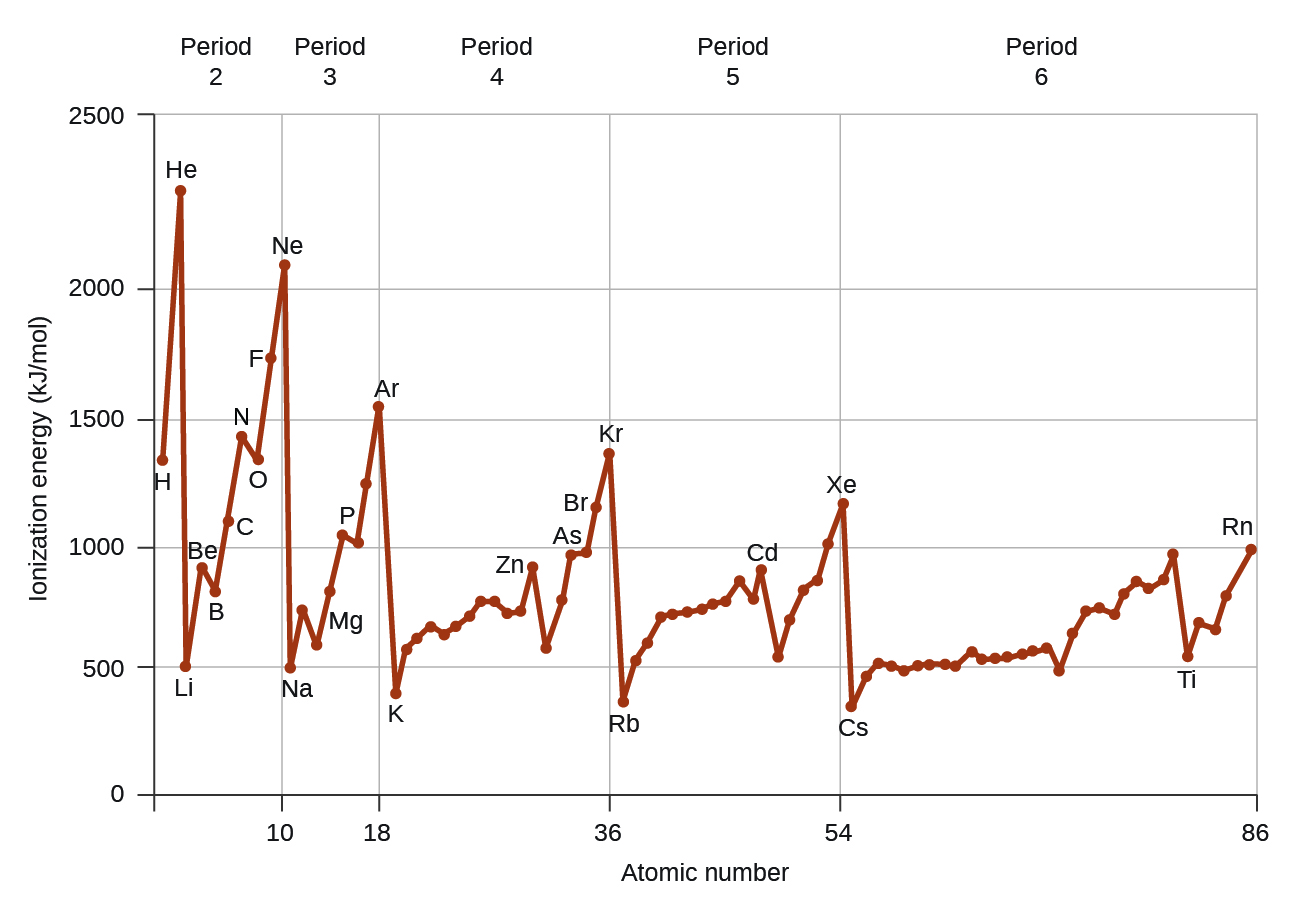
Another deviation occurs as orbitals become more than one-half filled. The first ionization energy for oxygen is slightly less than that for nitrogen, despite the trend in increasing IE1 values across a period. Looking at the orbital diagram of oxygen, we can see that removing one electron will eliminate the electron-electron repulsion caused by pairing the electrons in the 2p orbital and will result in a half-filled orbital (which is energetically favourable).

Removing an electron from a cation is more difficult than removing an electron from a neutral atom because of the greater electrostatic attraction to the cation. Likewise, removing an electron from a cation with a higher positive charge is more difficult than removing an electron from an ion with a lower charge. Thus, successive ionization energies for one element always increase. As seen in Table 10.6b, there is a large increase in the ionization energies (colour change) for each element. This jump corresponds to removal of the core electrons, which are harder to remove than the valence electrons. For example, Sc and Ga both have three valence electrons, so the rapid increase in ionization energy occurs after the third ionization.
| Element | IE1 | IE2 | IE3 | IE4 | IE5 | IE6 | IE7 |
|---|---|---|---|---|---|---|---|
| K | 418.8 | 3051.8 | 4419.6 | 5876.9 | 7975.5 | 9590.6 | 11343 |
| Ca | 589.8 | 1145.4 | 4912.4 | 6490.6 | 8153.0 | 10495.7 | 12272.9 |
| Sc | 633.1 | 1235.0 | 2388.7 | 7090.6 | 8842.9 | 10679.0 | 13315.0 |
| Ga | 578.8 | 1979.4 | 2964.6 | 6180 | 8298.7 | 10873.9 | 13594.8 |
| Ge | 762.2 | 1537.5 | 3302.1 | 4410.6 | 9021.4 | Not available | Not available |
| As | 944.5 | 1793.6 | 2735.5 | 4836.8 | 6042.9 | 12311.5 | Not available |
Example 10.6d
Ranking Ionization Energies
Predict the order of increasing energy for the following processes: IE1 for Al, IE1 for Tl, IE2 for Na, IE3 for Al.
Solution
Removing the 6p1 electron from Tl is easier than removing the 3p1 electron from Al because the higher n orbital is farther from the nucleus, so IE1(Tl) < IE1(Al). Ionizing the third electron from Al (Al2+ → Al3+ + e-) requires more energy because the cation Al2+ exerts a stronger pull on the electron than the neutral Al atom, so IE1(Al) < IE3(Al). The second ionization energy for sodium removes a core electron, which is a much higher energy process than removing valence electrons. Putting this all together, we obtain: IE1(Tl) < IE1(Al) < IE3(Al) < IE2(Na).
Exercise 10.6c
Which has the lowest value for IE1: O, Po, Pb, or Ba?
Check Your Answer[3]
Variation in Electron Affinities
The electron affinity [EA] is the energy change for the process of adding an electron to a gaseous atom to form an anion (negative ion).
[latex]\text{X}(g) + \text{e}^{-} \longrightarrow \text{X}^{-}(g) \;\;\;\;\; \text{EA}_1[/latex]
This process can be either endothermic (requiring energy) or exothermic (releasing energy), depending on the element. The EA of some of the elements is given in Figure 10.6f. You can see that some elements have negative values, whereas, other have positive values:
- Elements having negative values of EA tells us energy is released when the gaseous atom accepts an electron.
- Elements having positive values of EA means energy is required for the atom to become negatively charged.
Just as with ionization energy, subsequent EA values are associated with forming ions with more charge. The second EA is the energy associated with adding an electron to an anion to form a –2 ion, and so on.
As we might predict, it becomes easier to add an electron across a series of atoms as the effective nuclear charge of the atoms increases. We find, as we go from left to right across a period, EAs tend to become more negative. The exceptions found among the elements of group 2 (2A), group 15 (5A), and group 18 (8A) can be understood based on the electronic structure of these groups. The noble gases, group 18 (8A), have a completely filled shell and the incoming electron must be added to a higher n level, which is more difficult to do. Group 2 (2A) has a filled ns subshell, and so the next electron added goes into the higher energy np, so, again, the observed EA value is not as the trend would predict. Finally, group 15 (5A) has a half-filled np subshell and the next electron must be paired with an existing np electron. In all of these cases, the initial relative stability of the electron configuration disrupts the trend in EA.
We also might expect the atom at the top of each group to have the largest EA; their first ionization potentials suggest that these atoms have the largest effective nuclear charges. However, as we move down a group, we see that the second element in the group most often has the greatest EA. The reduction of the EA of the first member can be attributed to the small size of the n = 2 shell and the resulting large electron-electron repulsions. For example, chlorine, with an EA value of –348 kJ/mol, has the highest value of any element in the periodic table. The EA of fluorine is –322 kJ/mol. When we add an electron to a fluorine atom to form a fluoride anion (F–), we add an electron to the n = 2 shell. The electron is attracted to the nucleus, but there is also significant repulsion from the other electrons already present in this small valence shell. The chlorine atom has the same electron configuration in the valence shell, but because the entering electron is going into the n = 3 shell, it occupies a considerably larger region of space and the electron-electron repulsions are reduced. The entering electron does not experience as much repulsion and the chlorine atom accepts an additional electron more readily.
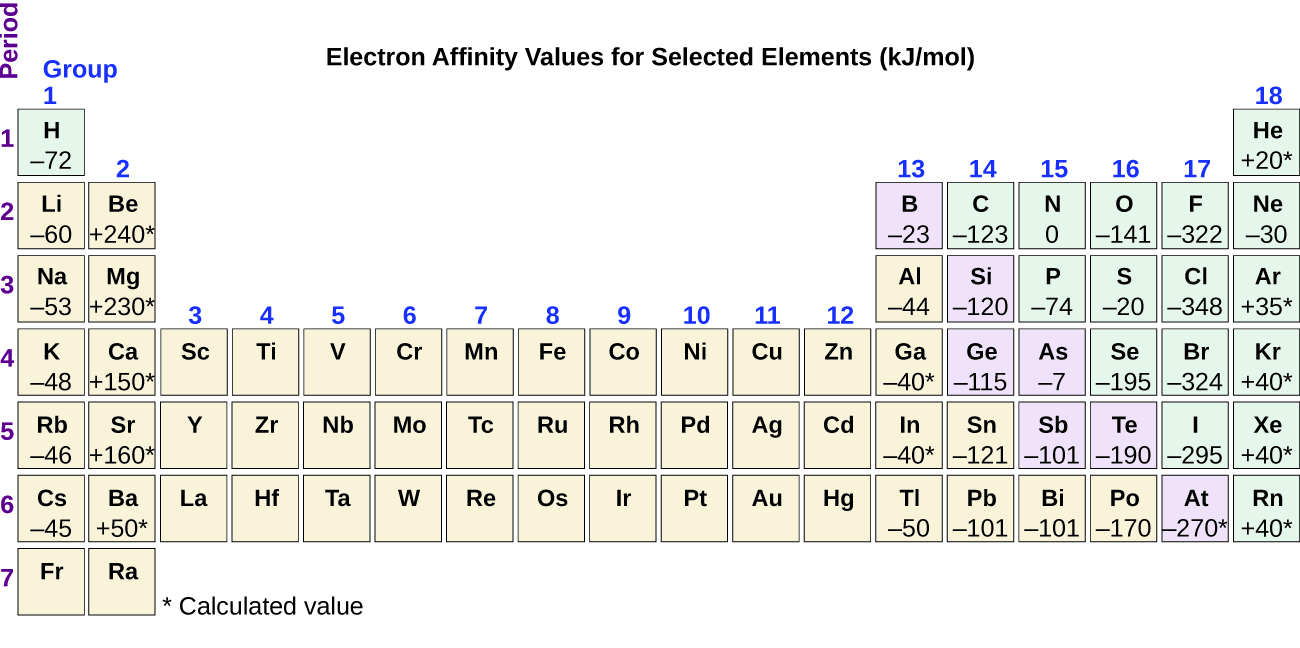
In summary, the electron affinity (EA) of an element is the energy change that occurs when an electron is added to a gaseous atom to give an anion. In general, elements with the most negative electron affinities (the highest affinity for an added electron) are those with the smallest size and highest ionization energies and are found in the upper right corner of the periodic table. With some exceptions to the rule, electron affinities become more negative across a row of the periodic table, which means they have a higher affinity for an electron. As you go down a group in the periodic table, atomic radius increases, ionization energy (affinity for their own valence electrons) decreases, and an atom's electron affinity for an added electron also decreases. Generally speaking,
The properties discussed in this section (size of atoms and ions, effective nuclear charge, ionization energies, and electron affinities) are central to understanding chemical reactivity. For example, because fluorine has an energetically favourable EA and a large energy barrier to ionization (IE), it is much easier to form fluorine anions than cations. Metallic properties including conductivity and malleability (the ability to be formed into sheets) depend on having electrons that can be removed easily. Thus, metallic character increases as we move down a group and decreases across a period is the same trend observed for atomic size because it is easier to remove an electron that is farther away from the nucleus. For both IE and electron affinity data, there are exceptions to the trends when dealing with completely filled or half-filled subshells.
For a summary on periodic table trends, watch The Periodic Table: Atomic Radius, Ionization Energy, and Electronegativity (7 min 52 sec).
Video Source: Professor Dave Explains. (2015, September 3). The Periodic table: Atomic radius, ionization energy, and electronegativity [Video]. YouTube.
Links to Interactive Learning Tools
Explore Periodictable.com's visualizations of the periodic trends discussed in this section (and many more trends). With just a few clicks, you can create three-dimensional versions of the periodic table showing atomic size or graphs of ionization energies from all measured elements.
Practice Periodic Trends from the Physics Classroom.
Attribution & References
Except where otherwise noted, this page is adapted by Jackie MacDonald from:
- "3.5 Periodic Variations in Element Properties" In General Chemistry 1 & 2 by Rice University, a derivative of Chemistry (Open Stax) by Paul Flowers, Klaus Theopold, Richard Langley & William R. Robinson and is licensed under CC BY 4.0. Access for free at Chemistry (OpenStax) / Adaptions and modifications were made to content for student comprehension.
- "6.5 Periodic Variations in Element Properties” In Chemistry 2e (Open Stax) by Paul Flowers, Klaus Theopold, Richard Langley & William R. Robinson is licensed under CC BY 4.0. Access for free at Chemistry 2e (Open Stax) .
-
- possible answers include Be, Li
- Order of decreasing covalent radius means ordering elements in order of Largest to smallest Radii. Here, the radius increases as we move down a group, so Fr>Cs. Next determine which is the next largest radii by comparing Na, Mg and Ca. Radius decreases as we move across a period, so Mg>Na. Since radius increases as we move down a group Ca>Mg. Putting the trends together, we obtain Fr>Cs>Ca>Mg>Na.
-
- F- < O2- < K+ < K < Cs2+ < Fr;
- Al3+ < Mg2+ < Ne < F- < O2-
- Ba has the lowest value for 1E1 ↵
one-half the distance between the nuclei of two identical atoms when they are joined by a covalent bond
charge that leads to the Coulomb force exerted by the nucleus on an electron, calculated as the nuclear charge minus shielding
group of ions or atoms that have identical electron configurations
energy required to remove an electron from a gaseous atom or ion; the associated number (e.g., second ionization energy) corresponds to the charge of the ion produced (X2+)
energy required to add an electron to a gaseous atom to form an anion

