1.4 Gerrymandering
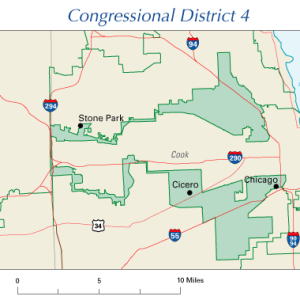
Some American States use IRCs to draw district boundaries. However, many other states allow the state legislature to draw borders. This can pose problems as elected officials often have an incentive to draw borders in a manner that is advantageous for their political party. This is known as gerrymandering. The Gerrymandering of electoral districts can lead to some strange configurations. One famous example is the oddly shaped 4th Congressional District of Illinois.
Why Gerrymander?
There are several motivations for manipulating district borders:
- Incumbency Protection – Drawing districts to increase the chances that an incumbent politician will get reelected.
- Racial Gerrymandering – Drawing districts in a manner that dilutes the political power of a racial or ethnic group.
- Partisan Gerrymandering – Drawing districts to ensure a numerical advantage for a political party.
Cracking and Packing
Two common tactics employed in gerrymandering are cracking and packing (MIT Election Data and Science Lab, 2025). Cracking is drawing districts in a manner that divides a group of voters into several districts, ensuring they don’t form a majority in any one district. Packing, on the other hand, involves drawing a district so that a numerically dominant voting group is confined to a single district. They will win that district easily, but they won’t be competitive elsewhere.
Try It: Gerrymandering

Image Description
A visual explanation of gerrymandering using coloured grids to represent voters and voting districts. The title reads “How to Steal an Election,” with a subtitle, “An introduction to gerrymandering, or how politicians pick their voters.”
On the left is a 10-by-6 grid with 60% yellow squares and 40% green squares, representing voters. The caption says, “Each square is a voter. Yellow party: 60%, Green party: 40%.”
To the right are two sets of the same grid, each divided into 5 voting districts in different ways:
The first grid is labelled “5 districts – fair outcome,” showing simple vertical slices where the yellow party wins 3 out of 5 districts (a 60/40 split).
The second grid is labelled “5 districts – rigged outcome,” showing irregular district shapes where the yellow party wins 4 out of 5 districts, overrepresenting their vote share.
Below are two more versions of the grid:
The left is labelled “Packing: 3 Yellow wins, 2 Green wins.” It groups almost all green voters into 2 districts (concentrating their votes), allowing yellow to narrowly win the remaining 3.
The right is labelled “Cracking: 5 Yellow wins.” It splits green voters across all districts, diluting their influence and giving yellow a win in every district.
The overall message shows how gerrymandering can unfairly influence election outcomes by redrawing district lines.
Note: You may need to reload the page for the activity to show
Activity Description
An interactive game where you draw the districts in order to get one colour to win the election
Benefits of Independent Redistricting
Gerrymandering can be described as a process in which the politicians choose their voters, which inverts the democratic ideal of having voters choose their representatives. The manipulation of district boundaries can have negative consequences for the political system. Aside from the tangible impact of denying groups from meaningful participation in the democratic process, it can increase cynicism and foster distrust in the political system. Conversely, Independent redistricting processes can provide transparency and offer meaningful opportunities for public participation (Sadhwani, 2022).

