Hai ví dụ về hàm bậc hai là [latex]p,q: \mathbb{R}^2 \rightarrow \mathbb{R}[/latex], với các giá trị

[latex]\begin{align*} p(x) &= 4x_1^2 + 2x_2^2 + 3x_1 x_2 +4x_1 + 5x_2 + 2\times 10^5 \end{align*}[/latex]

[latex]\begin{align*} q(x) &= 4x_1^2 - 2x_2^2 + 3x_1 x_2 +4x_1 + 5x_2 + 2\times 10^5 \end{align*}[/latex]

Hàm

[latex]\begin{align*} r(x) &= 4x_1^2 + 2x_2^2 + 3x_1 x_2 \end{align*}[/latex]

là một dạng toàn phương, vì nó không có các số hạng bậc nhất hay hằng số.

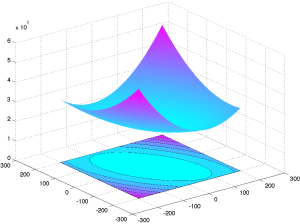	Tập mức và đồ thị của hàm bậc hai [latex]p[/latex]. Thượng đồ thị là bất kỳ phần nào nằm phía trên đồ thị theo hướng trục [latex]z[/latex]. Hàm này có ‘‘dạng hình bát’’, hay lồi.

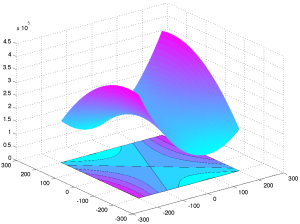	Tập mức và đồ thị của hàm bậc hai [latex]q[/latex]. Hàm bậc hai này không lồi.