31.1. Phép chiếu lên một đường thẳng thông qua tối đa hóa phương sai

Xét một tập dữ liệu gồm [latex]n[/latex] điểm [latex]x_j[/latex], [latex]j = 1, \cdots, n[/latex] trong [latex]\mathbb{R}^m[/latex]. Ta có thể biểu diễn tập dữ liệu này dưới dạng một ma trận [latex]m \times n[/latex] là [latex]X = [x_1, \cdots, x_n][/latex], trong đó mỗi [latex]x_j[/latex] là một véctơ cột [latex]m \times 1[/latex]. Mục tiêu của bài toán tối đa hóa phương sai là tìm một phương [latex]u \in \mathbb{R}^m[/latex] sao cho \textit{phương sai mẫu} của véctơ tương ứng [latex]u^TX = (u^Tx_1, \cdots, u^Tx_n)[/latex] là lớn nhất.

Nhắc lại rằng khi [latex]u[/latex] được chuẩn hóa, vô hướng [latex]u^Tx[/latex] là thành phần của [latex]x[/latex] dọc theo phương [latex]u[/latex], tức là nó tương ứng với phép chiếu của [latex]x[/latex] lên đường thẳng đi qua [latex]0[/latex] và có phương [latex]u[/latex].

Ở đây, ta tìm một phương đã được chuẩn hóa [latex]u[/latex] sao cho phương sai thực nghiệm của các giá trị được chiếu [latex]u^Tx_j[/latex], [latex]j = 1, \cdots, n[/latex], là lớn. Nếu [latex]\hat{x}[/latex] là véctơ trung bình của các [latex]x_j[/latex], thì giá trị trung bình của các giá trị được chiếu là [latex]u^T\hat{x}[/latex]. Do đó, phương có phương sai lớn nhất là phương giải bài toán tối ưu hóa

[latex]\begin{align*} \max\limits_{u: ||u||_2=1} \frac{1}{n} \sum\limits_{j=1}^n \left((x_j-\hat{x})^Tu\right)^2. \end{align*}[/latex]

Bài toán trên có thể được phát biểu là

[latex]\begin{align*} \max\limits_{u: ||u||_2=1} u^T {\textstyle \Sigma} u, \end{align*}[/latex]

trong đó

[latex]\begin{align*} {\textstyle \Sigma} := \frac{1}{n}\sum\limits_{j=1}^n (x_j - \hat{x}) (x_j-\hat{x})^T \end{align*}[/latex]

là ma trận hiệp phương sai mẫu cỡ [latex]m \times m[/latex] của dữ liệu.

Ta đã gặp bài toán trên trước đây, dưới tên gọi thương Rayleigh của một ma trận đối xứng. Việc giải bài toán chỉ đơn giản là tìm một véctơ riêng của ma trận hiệp phương sai [latex]\Sigma[/latex] tương ứng với giá trị riêng lớn nhất.

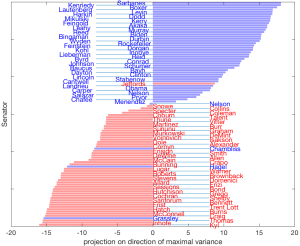Phương có phương sai lớn nhất cho dữ liệu bỏ phiếu của Thượng viện. Hình ảnh này cho thấy điểm số được gán cho mỗi Thượng nghị sĩ dọc theo phương có phương sai lớn nhất, [latex]u^T_{\max}(x_j-\hat{x})[/latex], [latex]j = 1, \cdots, n[/latex], với [latex]u_{\max}[/latex] là một véctơ riêng đã chuẩn hóa tương ứng với giá trị riêng lớn nhất của ma trận hiệp phương sai [latex]\Sigma[/latex]. Các Thượng nghị sĩ Đảng Cộng hòa có xu hướng nhận điểm âm, trong khi ta thấy nhiều Thượng nghị sĩ Đảng Dân chủ có điểm dương (rõ ràng dấu ở đây không quan trọng, vì ta có thể đổi [latex]u[/latex] thành [latex]-u[/latex]; chỉ có thứ tự là quan trọng). Do đó, phương này có thể được diễn giải là tiết lộ sự liên kết đảng phái. Hai Thượng nghị sĩ thuộc nhóm đối lập (đặc biệt là Thượng nghị sĩ Chaffee) thực sự đã đôi khi bỏ phiếu chống lại đảng của mình.

Lưu ý rằng điểm số tuyệt đối lớn nhất thu được trong đồ thị này lớn hơn khoảng 18 lần so với điểm số quan sát được trên phép chiếu lên một phương ngẫu nhiên. Điều này phù hợp với thực tế rằng phương hiện tại có phương sai lớn nhất.

31.2. Phân tích phần tử chính quy

Ý tưởng chính

Ý tưởng chính đằng sau \textit{phân tích thành phần chính} là trước hết tìm một phương tương ứng với phương sai lớn nhất giữa các điểm dữ liệu. Dữ liệu sau đó được chiếu lên siêu phẳng trực giao với phương đó. Ta thu được một tập dữ liệu mới và tìm một phương mới có phương sai lớn nhất. Ta có thể dừng quá trình này khi đã thu thập đủ số phương (ví dụ, ba phương nếu ta muốn trực quan hóa dữ liệu trong không gian 3D).

Thực tế là các phương được tìm thấy theo cách này chính là các véctơ riêng của ma trận hiệp phương sai của dữ liệu. Thuật ngữ \textit{thành phần chính} đề cập đến các phương được cho bởi các véctơ riêng này. Về mặt toán học, quá trình này do đó tương đương với việc tìm phân tích giá trị riêng của một ma trận nửa xác định dương, chính là ma trận hiệp phương sai của các điểm dữ liệu.

Phép chiếu lên một mặt phẳng

Phép chiếu được sử dụng để thu được, chẳng hạn, một cái nhìn hai chiều với phương sai lớn nhất, có dạng [latex]x \rightarrow Px[/latex], trong đó [latex]P=[u_1, u_2]^T[/latex] là một ma trận chứa các véctơ riêng tương ứng với hai giá trị riêng đầu tiên.

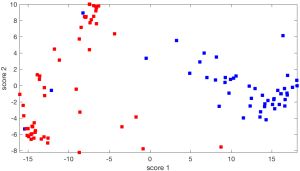Phép chiếu hai chiều của ma trận bỏ phiếu Thượng viện: Phép chiếu phẳng cụ thể này sử dụng hai véctơ riêng tương ứng với hai giá trị riêng lớn nhất của ma trận hiệp phương sai của dữ liệu. Dường như nó cho phép phân cụm các Thượng nghị sĩ theo đảng phái và do đó cung cấp nhiều thông tin hơn so với, chẳng hạn, mặt phẳng tương ứng với hai giá trị riêng nhỏ nhất.

31.3. Phương sai giải được

Tổng phương sai trong dữ liệu được định nghĩa là tổng các phương sai của các thành phần riêng lẻ. Đại lượng này chỉ đơn giản là \textit{vết} của ma trận hiệp phương sai vì các phần tử trên đường chéo của ma trận này chứa các phương sai. Nếu [latex]\Sigma[/latex] có phân tích giá trị riêng (EVD) là [latex]\Sigma = U \Lambda U^T[/latex], trong đó [latex]\Lambda = {\bf diag}(\lambda_1, \cdots, \lambda_m)[/latex] chứa các giá trị riêng, và [latex]U[/latex] là một ma trận trực giao của các véctơ riêng, thì tổng phương sai có thể được biểu diễn dưới dạng tổng của tất cả các giá trị riêng:

[latex]\begin{align*} {\bf Tr} \Sigma = {\bf Tr}(U\Lambda U^T) = {\bf Tr} (U^TU\Lambda) = {\bf Tr} \Lambda = \lambda_1 + \cdots + \lambda_n. \end{align*}[/latex]

Khi ta chiếu dữ liệu lên một mặt phẳng hai chiều tương ứng với các véctơ riêng [latex]u_1, u_2[/latex] được liên kết với hai giá trị riêng lớn nhất [latex]\lambda_1, \lambda_2[/latex], ta nhận được một ma trận hiệp phương sai mới [latex]P \Sigma P^T[/latex], trong đó [latex]P = [u_1, u_2]^T[/latex]. Tổng phương sai của dữ liệu được chiếu là

[latex]\begin{align*} {\bf Tr}(P\Sigma P^T) = \lambda_1 + \lambda_2. \end{align*}[/latex]

Do đó, ta có thể định nghĩa tỷ lệ phương sai “giải thích được” bởi dữ liệu được chiếu là tỷ lệ:

[latex]\begin{align*} \frac{\lambda_1 + \lambda_2}{\lambda_1 + \cdots + \lambda_n}. \end{align*}[/latex]

Nếu tỷ lệ này cao, ta có thể nói rằng phần lớn sự biến thiên trong dữ liệu có thể được quan sát trên mặt phẳng được chiếu.

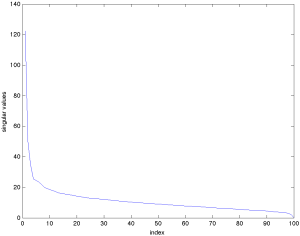Hình ảnh này cho thấy các giá trị riêng của ma trận hiệp phương sai [latex]m \times m[/latex] của dữ liệu bỏ phiếu Thượng viện, chứa hiệp phương sai giữa các phiếu bầu của mỗi cặp Thượng nghị sĩ. Rõ ràng, các giá trị riêng giảm rất nhanh. Trong trường hợp này, tỷ lệ phương sai giải thích được so với tổng phương sai gần [latex]90%[/latex], điều này cho thấy “hầu hết thông tin” nằm trong giá trị riêng đầu tiên. Vì véctơ riêng tương ứng gần như tương ứng với một “đường lối đảng phái” hoàn hảo, ta có thể nói rằng sự liên kết đảng phái giải thích hầu hết phương sai trong dữ liệu bỏ phiếu của Thượng viện.