30.1. Các định nghĩa

Với một ma trận đối xứng cho trước [latex]A\in \mathbb{R}^{n\times n}[/latex], dạng toàn phương tương ứng là hàm [latex]q: \mathbb{R}^n \rightarrow \mathbb{R}[/latex] với các giá trị

[latex]\begin{align*}q(x) = x^TAx.\end{align*}[/latex]

• Một ma trận đối xứng [latex]A[/latex] được gọi là \textit{nửa xác định dương} (PSD, ký hiệu: [latex]A \succeq 0[/latex]) khi và chỉ khi dạng toàn phương tương ứng [latex]q[/latex] không âm với mọi [latex]x[/latex]:

[latex]\begin{align*}q(x) \ge 0 \quad (\forall x\in \mathbb{R}^n).\end{align*}[/latex]

• Ma trận thoả mãn điểu kiện trên được gọi là xác định dương (PD, ký hiệu: [latex]A \succ 0[/latex]) nếu dạng toàn phương này không âm và xác định, tức là, [latex]q(x) = 0[/latex] khi và chỉ khi [latex]x=0[/latex].

Một ma trận là nửa xác định dương khi và chỉ khi các giá trị riêng của [latex]A[/latex] là không âm. Do đó, ta có thể kiểm tra xem một dạng có phải là nửa xác định dương không bằng cách tính phân tích giá trị riêng của ma trận đối xứng nền.

Định lý: Các giá trị riêng của ma trận nửa xác định dương

Chứng minh. 

Theo định nghĩa, các tính chất nửa xác định dương và xác định dương chỉ là các tính chất của giá trị riêng của ma trận, không phải của véctơ riêng. Ngoài ra, nếu ma trận [latex]A[/latex] cỡ [latex]n \times n[/latex] là nửa xác định dương, thì với mọi ma trận [latex]B[/latex] có [latex]n[/latex] cột, ma trận [latex]B^TAB[/latex] cũng vậy.

30.2. Các trường hợp đặc biệt và ví dụ

Dyad đối xứng

Các trường hợp đặc biệt của ma trận nửa xác định dương bao gồm các dyad đối xứng. Thật vậy, nếu [latex]A = uu^T[/latex] với một véctơ [latex]u \in \mathbb{R}^n[/latex] nào đó, thì với mọi [latex]x[/latex]:

[latex]\begin{align*}q_A(x) = x^Tuu^Tx = (u^Tx)^2 \ge 0.\end{align*}[/latex]

Tổng quát hơn, nếu [latex]B \in \mathbb{R}^{m\times n}[/latex], thì [latex]A = B^TB[/latex] là nửa xác định dương, vì

[latex]\begin{align*}q_A(x) = x^TB^TBx = ||Bx||_2^2 \ge 0.\end{align*}[/latex]

Ma trận đường chéo

Một ma trận đường chéo là nửa xác định dương (tương ứng, xác định dương) khi và chỉ khi tất cả các phần tử trên đường chéo của nó là không âm (tương ứng, dương).

Ví dụ về các ma trận nửa xác định dương

• Ma trận hiệp phương sai.
• Ma trận Laplace của một đồ thị.
• Ma trận Gram của các điểm dữ liệu.

30.3. Căn bậc hai và phân tích Cholesky

Đối với ma trận xác định dương, ta có thể tổng quát hóa khái niệm căn bậc hai thông thường của một số không âm. Thật vậy, nếu [latex]A[/latex] là nửa xác định dương, tồn tại một ma trận nửa xác định dương duy nhất, ký hiệu là [latex]A^{1/2}[/latex], sao cho [latex]A = (A^{1/2})^2[/latex]. Ta có thể biểu diễn căn bậc hai ma trận này theo phân tích giá trị riêng đối xứng (SED) của [latex]A = U \Lambda U^T[/latex], là [latex]A^{1/2} = U \Lambda^{1/2} U^T[/latex], trong đó [latex]\Lambda^{1/2}[/latex] được thu từ [latex]\Lambda[/latex] bằng cách lấy căn bậc hai của các phần tử trên đường chéo của nó. Nếu [latex]A[/latex] là xác định dương, thì căn bậc hai của nó cũng vậy.

Bất kỳ ma trận nửa xác định dương nào cũng có thể được viết dưới dạng tích [latex]A= LL^T[/latex] với một ma trận [latex]L[/latex] thích hợp. Phép phân tích này không duy nhất, và [latex]L = A^{1/2}[/latex] chỉ là một lựa chọn khả dĩ (và là lựa chọn duy nhất nửa xác định dương). Một lựa chọn khác, theo phân tích SED của [latex]A = U \Lambda U^T[/latex], là [latex]L = U \Lambda^{1/2} U^T[/latex]. Nếu [latex]A[/latex] là xác định dương, thì ta có thể chọn [latex]L[/latex] là ma trận tam giác dưới và khả nghịch. Phép phân tích khi đó được gọi là \textit{phân tích Cholesky} của [latex]A[/latex].

30.4. Ellipsoids

Có một sự tương ứng chặt chẽ giữa các elipsoid và các ma trận nửa xác định dương.

Định nghĩa

Ta định nghĩa một elipsoid là một phép biến đổi afin của quả cầu đơn vị đối với chuẩn Euclid:

[latex]\begin{align*}{\bf E} = \{\hat{x} +Lz: ||z||_2 \leq 1 \},\end{align*}[/latex]

trong đó [latex]L \in \mathbb{R}^{n\times n}[/latex] là một ma trận không suy biến bất kỳ. Ta có thể biểu diễn elipsoid là

[latex]\begin{align*} \mathbf{E}=\left\{x:\left\|L^{-1}(x-\hat{x})\right\|_2 \leq 1\right\}=\left\{x:(x-\hat{x})^T A^{-1}(x-\hat{x}) \leq 1\right\},\end{align*}[/latex]

trong đó [latex]A: = L^T L^{-1}[/latex] là ma trận xác định dương.

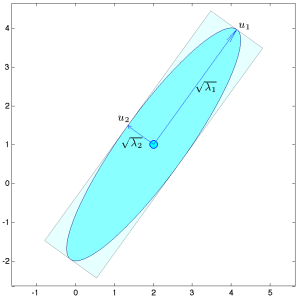
Diễn giải hình học thông qua phân tích giá trị riêng đối xứng (SED)

Ta có thể diễn giải các véctơ riêng và các giá trị riêng tương ứng của [latex]A[/latex] theo các tính chất hình học của elipsoid như sau. Xét phân tích SED của [latex]A[/latex]: [latex]A = U \Lambda U^T[/latex], với [latex]U^T U = I[/latex] và [latex]\Lambda[/latex] là ma trận đường chéo, với các phần tử trên đường chéo là dương. Phân tích SED của ma trận nghịch đảo của nó là [latex]A^{-1} = LL^T = U \Lambda^{-1} U^T[/latex]. Đặt [latex]\tilde{x} = U^T(x- \hat{x})[/latex]. Ta có thể biểu diễn điều kiện [latex]x \in {\bf E}[/latex] là

[latex]\begin{align*}\tilde{x}^T\Lambda \tilde{x} = \sum\limits_{i=1}^n \lambda_i \tilde{x}_i^2 \leq 1.\end{align*}[/latex]

Bây giờ đặt [latex]\overline{x}_i = \sqrt{\lambda_i} \tilde{x}_i[/latex], [latex]i = 1, \cdots, n[/latex]. Biểu thức trên có thể được viết là [latex]\overline{x}^T \overline{x} \leq 1[/latex]: trong không gian [latex]\overline{x}[/latex], elipsoid chỉ đơn giản là một quả cầu đơn vị. Trong không gian [latex]\tilde{x}[/latex], elipsoid tương ứng với việc co giãn mỗi trục [latex]\overline{x}[/latex] theo căn bậc hai của các giá trị riêng. Elipsoid có các trục chính song song với các trục tọa độ trong không gian [latex]\tilde{x}[/latex]. Sau đó ta áp dụng một phép quay và một phép tịnh tiến để có được elipsoid trong không gian [latex]x[/latex] ban đầu. Phép quay được xác định bởi các véctơ riêng của [latex]A^{-1}[/latex], vốn nằm trong ma trận trực giao [latex]U[/latex]. Do đó, hình học của elipsoid có thể được đọc từ phân tích SED của ma trận xác định dương [latex]A^{-1} = LL^T[/latex]: các véctơ riêng cho ta các phương chính, và độ dài các bán trục là căn bậc hai của các giá trị riêng.

	Đồ thị bên trái cho thấy elipsoid [latex]\{\hat{x} +Lz: ||z||_2 \leq 1 \}[/latex], với
	[latex]\begin{align*}\hat{x}=\left(\begin{array}{l} 2 \\ 1 \end{array}\right), \quad L=\left(\begin{array}{ll} 1 & 2 \\ 0 & 3 \end{array}\right) \text {. }\end{align*}[/latex]
	Ma trận [latex]LL^T[/latex] có phân tích SED
	[latex]\begin{align*} L L^T &= U^T \Lambda U, \end{align*}[/latex]
	với
	[latex]\begin{align*} U &= \left(\begin{array}{cc} -0.9871 & 0.1602 \\ 0.1602 & 0.9871 \end{array}\right), \\ \Lambda &= \left(\begin{array}{cc} 0.6754 & 0 \\ 0 & 13.3246 \end{array}\right). \end{align*}[/latex]
	Ta kiểm tra rằng các cột của [latex]U[/latex] xác định các phương chính, và [latex]\sqrt{\lambda_1} = 3.6503[/latex], [latex]\sqrt{\lambda_2} = 0.8219[/latex] là độ dài các bán trục.

Phần trên đặc biệt cho thấy rằng một biểu diễn tương đương của một elipsoid là

[latex]\begin{align*}\{x: (x-\hat{x})^TB(x-\hat{x}) \leq 1 \}\end{align*}[/latex]

trong đó [latex]B:=A^{-1}[/latex] is PD.

Như vậy chúng ta có thể định nghĩa các elipsoid suy biến, tương ứng với các trường hợp khi ma trận [latex]B[/latex] ở trên, hoặc ma trận nghịch đảo [latex]A[/latex] của nó, là suy biến. Ví dụ, các hình trụ hoặc các lát cắt (giao của hai nửa không gian song song) là các elipsoid suy biến.