18.1. Tổng quan

Chụp cắt lớp là công nghệ tái tạo một hình ảnh từ các mặt cắt của nó. Từ này bắt nguồn từ tiếng Hy Lạp ‘‘tomos’’ (‘‘lát cắt’’) và ‘‘graph’’ (‘‘mô tả’’). Bài toán này nảy sinh trong nhiều lĩnh vực, từ thiên văn học đến hình ảnh y khoa.

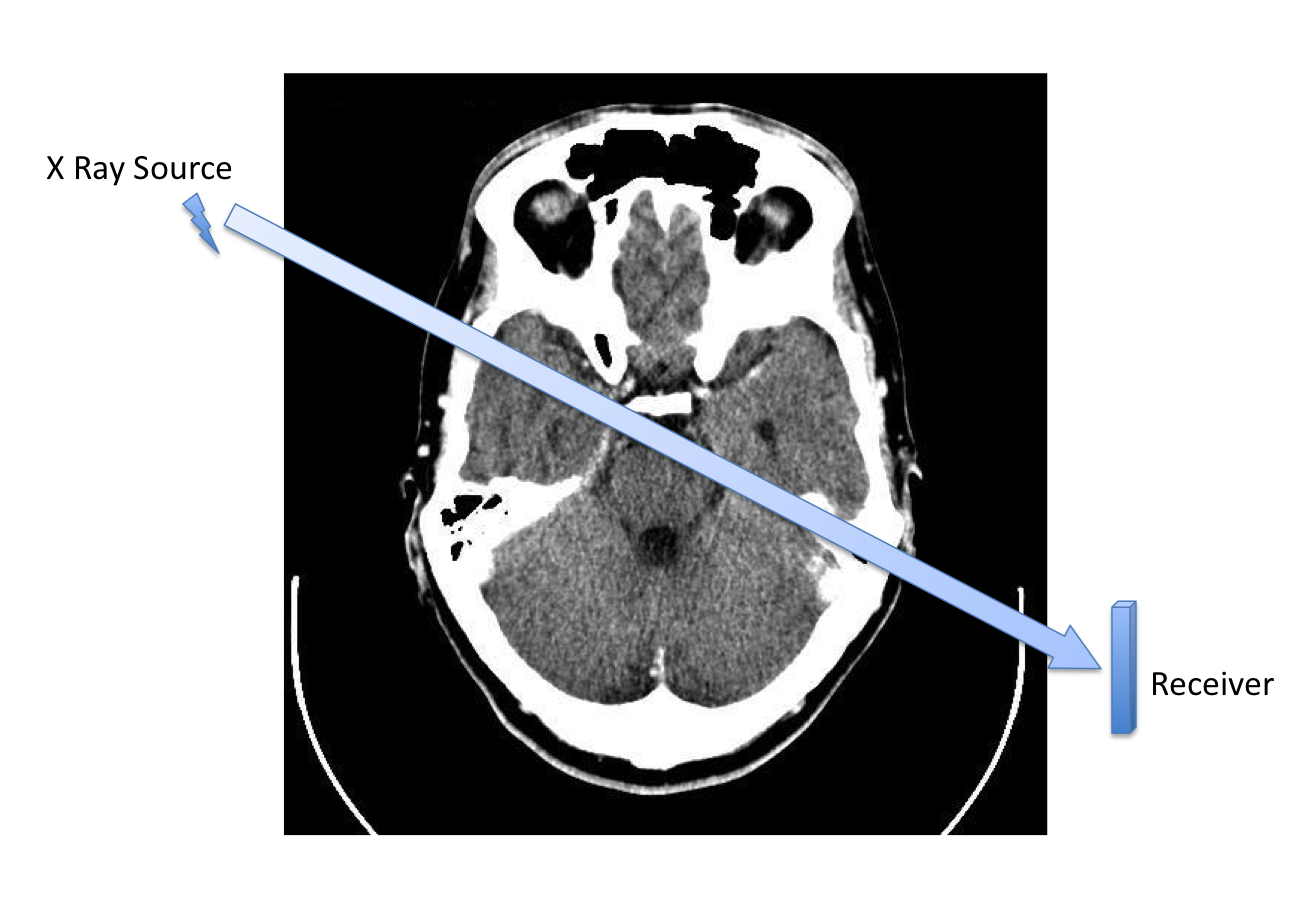
Chụp cắt lớp vi tính theo trục (CAT) là một phương pháp hình ảnh y khoa xử lý một lượng lớn các hình ảnh tia X hai chiều để tạo ra một hình ảnh ba chiều. Mục tiêu là để hình dung, ví dụ, mật độ mô của các phần khác nhau của bộ não, nhằm phát hiện các bất thường (chẳng hạn như khối u não).

Thông thường, các hình ảnh tia X biểu diễn các ‘‘lát cắt’’ của bộ phận cơ thể (như bộ não) được kiểm tra. Những lát cắt đó thu được một cách gián tiếp thông qua các phép đo theo trục về sự suy giảm của tia X, như được giải thích bên dưới. Do đó, trong CAT cho hình ảnh y khoa, chúng ta sử dụng các phép đo theo trục (đường thẳng) để có được các hình ảnh hai chiều (lát cắt), và từ việc quét các hình ảnh đó, chúng ta có thể tiến hành tái tạo kỹ thuật số một khung cảnh ba chiều. Ở đây, chúng ta tập trung vào quá trình tạo ra một hình ảnh hai chiều duy nhất từ các phép đo theo trục.

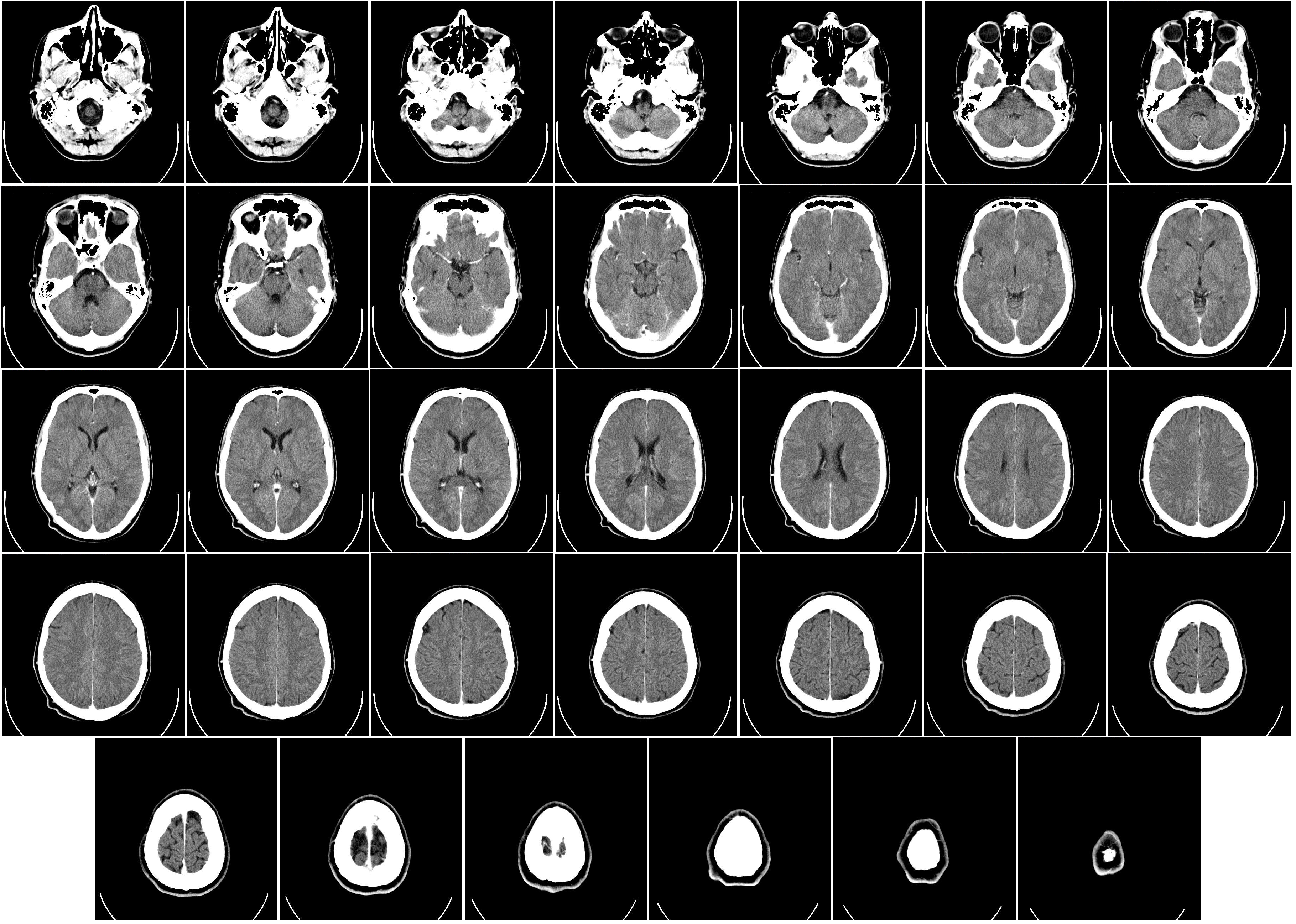
	Một bộ sưu tập các ‘‘lát cắt’’ của não người thu được bằng chụp cắt lớp vi tính. Các hình ảnh này cho thấy mật độ của mô ở các phần khác nhau của não. Mỗi lát cắt thực chất là một hình ảnh được tái tạo thu được bằng kỹ thuật chụp cắt lớp được giải thích bên dưới. Bộ sưu tập các lát cắt này lần lượt có thể được sử dụng để tạo thành một biểu diễn ba chiều đầy đủ của bộ não.
	Nguồn: Wikipedia entry.

18.2 Từ 1D đến 2D: chụp cắt lớp theo trục

Trong hình ảnh y khoa dựa trên CAT, một số tia X được chiếu xuyên qua các mô cần kiểm tra theo các hướng khác nhau, và cường độ của chúng sau khi đi qua các mô được ghi lại bằng máy ảnh. Đối với mỗi hướng, chúng ta ghi lại sự suy giảm của tia X, bằng cách so sánh cường độ của tia X tại nguồn, [latex]I_{nguồn}[/latex], với cường độ sau khi tia X đã đi qua các mô, tại đầu thu, [latex]I_{thu}[/latex].

	Một lát cắt duy nhất thu được bằng chụp cắt lớp vi tính. Mỗi lát cắt là một hình ảnh được tái tạo thu được bằng cách ghi lại sự suy giảm của tia X qua các mô dọc theo vô số hướng. Hình ảnh cho thấy nguồn tia X và đầu thu tương ứng được sử dụng để đo sự suy giảm dọc theo một hướng cụ thể.

18.3. Phương trình tuyến tính cho một lát cắt

Tương tự như định luật Beer-Lambert trong quang học, hóa ra, với một mức độ xấp xỉ hợp lý, tỉ số logarit của cường độ tại nguồn và tại máy thu là tuyến tính theo mật độ của các mô mà tia đi qua.

	Ta xét một phiên bản rời rạc hóa của một hình ảnh lát cắt vuông, với [latex]N \times N[/latex] pixel có các giá trị thang độ xám. Trong ví dụ được minh họa ở đây, ta chỉ đơn giản có [latex]N = 2[/latex], và tổng cộng bốn pixel. Mỗi pixel có thể được biểu diễn bằng một cặp chỉ số [latex](i, j)[/latex], với [latex]1 \leq i, j \leq N[/latex]. Các giá trị thang độ xám biểu thị mật độ của các mô, với [latex]d_{ij}[/latex] là mật độ tại pixel [latex](i, j)[/latex].

Với việc rời rạc hóa, mối quan hệ tuyến tính giữa tỉ số logarit của cường độ và mật độ có thể được biểu diễn là

[latex]y = \log{ \dfrac{ I_{thu} }{ I_{nguồn} } } = \sum_{(i, j) \in T} A_{ij} d_{ij},[/latex]

trong đó [latex]T[/latex] ký hiệu các chỉ số của các vùng pixel mà tia X đi qua, [latex]d_{ij}[/latex] là mật độ trong vùng [latex](i, j)[/latex], và [latex]A_{ij}[/latex] là tỉ lệ diện tích bên trong pixel [latex](i,j)[/latex] mà tia đi qua.

	Quan hệ tuyến tính giữa các tỉ số log-cường độ quan sát được [latex]y_1, y_2, y_3, y_4[/latex] và các mật độ (không quan sát được) [latex]d_{ij}, 1 \leq i, j \leq 2[/latex] trong bốn pixel. Mũi tên chéo tương ứng với một tia X đi qua khoảng [latex]\dfrac{2}{3}[/latex] diện tích của các pixel [latex](1, 1)[/latex] và [latex](2, 2)[/latex], và [latex]\dfrac{1}{3}[/latex] diện tích của các pixel [latex](1, 2)[/latex] và [latex](2, 1)[/latex].

Do đó, ta có thể liên hệ véctơ [latex]d \in \mathbb{R}^{N^2}[/latex] với véctơ tỉ số log-cường độ quan sát được [latex]y \in \mathbb{R}^m[/latex] dưới dạng một phương trình tuyến tính

[latex]\begin{align*} y = Ad \end{align*}[/latex]

trong đó [latex]A \in \mathbb{R}^{m \times n}[/latex], với [latex]n := N^2[/latex]. Lưu ý rằng tùy thuộc vào số lượng pixel được sử dụng và số lượng phép đo, ma trận [latex]A[/latex] có thể khá lớn. Tổng quát, ma trận này là ma trận rộng, theo nghĩa là nó có (nhiều) cột hơn hàng ([latex]n \gg m[/latex]). Do đó, hệ phương trình trên thường là không xác định.

Trong ví dụ được minh họa ở trên, ta có

[latex]\begin{align*} \begin{pmatrix} y_1 \\ y_2 \\ y_3 \\ y_4 \end{pmatrix} = \begin{pmatrix} 1 & 1 & 0 & 0 \\ 0 & 0 & 1 & 1 \\[0.9ex] \dfrac{2}{3} & \dfrac{1}{3} & \dfrac{1}{3} & \dfrac{2}{3} \\[2ex] 1 & 0 & 1 & 0 \end{pmatrix} \begin{pmatrix} d_{11} \\ d_{12} \\ d_{21} \\ d_{22} \end{pmatrix} \nonumber \end{align*}[/latex]

18.4. Các vấn đề đặt ra

Ví dụ trên thúc đẩy chúng ta giải quyết các bài toán về giải hệ phương trình tuyến tính. Nó cũng đặt ra vấn đề về sự tồn tại (chúng ta có đủ phép đo để tìm ra mật độ không?) và tính duy nhất (nếu một nghiệm tồn tại, liệu nó có duy nhất không?).