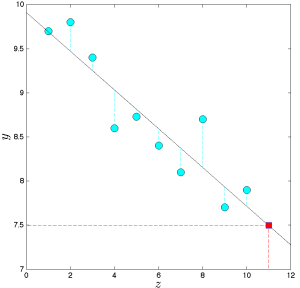
Hồi quy tuyến tính dựa trên ý tưởng khớp một hàm tuyến tính qua các điểm dữ liệu.
Ở dạng cơ bản, bài toán được phát biểu như sau. Ta được cho các dữ liệu [latex](y_i, x_i), i=1, \ldots, m[/latex] trong đó [latex]x_i \in \mathbb{R}^n[/latex] là “đầu vào” và [latex]y_i \in \mathbb{R}[/latex] là “đầu ra” cho phép đo thứ [latex]i[/latex]. Ta tìm một hàm tuyến tính [latex]f: \mathbb{R}^n \to \mathbb{R}[/latex] sao cho các giá trị [latex]f(x_i)[/latex] gần với các giá trị [latex]y_i[/latex] tương ứng.
Trong hồi quy bình phương tối thiểu, cách ta đánh giá một hàm ứng viên [latex]f[/latex] khớp với dữ liệu tốt đến đâu là thông qua chuẩn Euclid (bình phương):
$$
\sum_{i=1}^m\left(y_i-f\left(x_i\right)\right)^2 .
$$
Vì một hàm tuyến tính [latex]f[/latex] có dạng [latex]f(x)=\theta^T x[/latex] với một véctơ [latex]\theta \in \mathbb{R}^n[/latex] nào đó, bài toán tối thiểu hóa tiêu chuẩn trên có dạng
$$
\min _\theta \sum_{i=1}^m\left(y_i-x_i^T \theta\right)^2 .
$$
Ta có thể phát biểu bài toán này dưới dạng một bài toán bình phương tối thiểu:
$$
\min _\theta\|A \theta-y\|_2,
$$
trong đó
$$
A=\left(\begin{array}{c}
x_1^T \\
\vdots \\
x_m^T
\end{array}\right)
$$
The linear regression approach can be extended to multiple dimensions, that is, to problems where the output in the above problem contains more than one dimension (see ). It can also be extended to the problem of fitting non-linear curves.
Phương pháp hồi quy tuyến tính có thể được mở rộng cho nhiều chiều, tức là cho các bài toán mà đầu ra trong bài toán trên có nhiều hơn một chiều (xem tại đây ). Nó cũng có thể được mở rộng cho bài toán khớp các đường cong phi tuyến.
 |
Trong ví dụ này, ta tìm cách phân tích phản ứng của khách hàng đối với việc tăng giá của một mặt hàng nhất định. Ta được cho các điểm dữ liệu hai chiều [latex]\left(x_i, y_i\right), i=1, \ldots, m[/latex]. Các giá trị [latex]x_i[/latex] chứa giá của mặt hàng, và các giá trị [latex]y_i[/latex] là số lượng khách hàng trung bình mua mặt hàng ở mức giá đó. |
| Phương trình tổng quát của một đường thẳng không thẳng đứng là [latex]y=\theta_1 x+\theta_2[/latex], trong đó [latex]\theta=\left(\theta_1, \theta_2\right)[/latex] chứa các biến quyết định. Chất lượng của việc khớp một đường thẳng tổng quát được đo bằng tổng bình phương sai số ở thành phần [latex]y[/latex] (các đường chấm màu xanh). Do đó, sự khớp bình phương tối thiểu tốt nhất được thu được thông qua bài toán bình phương tối thiểu | |
| $$ \min _\theta \sum_{i=1}^m\left(\theta_1 x_i+\theta_2-y_i\right)^2 . $$ |
|
| Một khi đường thẳng được tìm thấy, nó có thể được sử dụng để dự báo giá trị của số lượng khách hàng trung bình mua mặt hàng ([latex]y[/latex]) cho một mức giá mới ([latex]x[/latex]). Dự báo được thể hiện bằng màu đỏ. |
Xem thêm:
