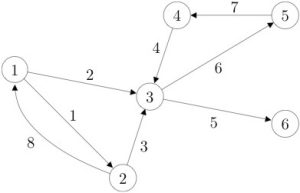
Về mặt toán học, một mạng lưới là một đồ thị gồm [latex]m[/latex] nút được nối với nhau bởi [latex]n[/latex] cung có hướng. Ở đây, ta giả sử rằng các cung là các cặp có thứ tự, với tối đa một cung nối hai nút bất kỳ; ta cũng giả sử rằng không có khuyên (cung từ một nút đến chính nó). Ta không giả sử các cạnh của đồ thị có trọng số, nghĩa là mỗi cạnh đều như nhau.

Ta có thể mô tả đầy đủ mạng lưới bằng \textit{ma trận liên thuộc cung-nút}, là ma trận cỡ [latex]m \times n[/latex] được định nghĩa là

[latex]A_{ij} = \begin{cases} 1 & \text{nếu cung } j \text{ bắt đầu tại nút } i \\ -1 & \text{nếu cung } j \text{ kết thúc tại nút } i \\ 0 & \text{ngược lại.} \end{cases} , \quad 1 \le i \le m, \quad 1 \le j \le n.[/latex]

Hình vẽ cho thấy đồ thị tương ứng với ma trận liên thuộc cung-nút \[ A = \left[ \begin{array}{cccccccc} 1 & 1 & 0 & 0 & 0 & 0 & 0 & -1 \\ -1 & 0 & 1 & 0 & 0 & 0 & 0 & 1 \\ 0 & -1 & -1 & -1 & 1 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 & -1 & 0 \\ 0 & 0 & 0 & 0 & 0 & -1 & 1 & 0 \\ 0 & 0 & 0 & 0 & -1 & 0 & 0 & 0 \\ \end{array} \right]. \]

Xem thêm: Luồng mạng.