• Siêu phẳng
• Phép chiếu lên siêu phẳng
• Hình học của siêu phẳng
• Bán không gian

5.1. Siêu phẳng

Một siêu phẳng là một tập hợp được mô tả bằng một đẳng thức tích vô hướng duy nhất. Chính xác hơn, một siêu phẳng trong [latex]\mathbb{R}^n[/latex] là một tập hợp có dạng
[latex]\begin{align*} \mathbf{H} = {x: a^Tx = b}, \end{align*}[/latex]
trong đó [latex]a \in \mathbb{R}^n[/latex], [latex]a \neq 0[/latex], và [latex]b \in \mathbb{R}[/latex] được cho. Khi [latex]b=0[/latex], siêu phẳng đơn giản là tập hợp các điểm trực giao với [latex]a[/latex]; khi [latex]b \neq 0[/latex], siêu phẳng là một phép tịnh tiến, theo hướng [latex]a[/latex], của tập hợp đó.

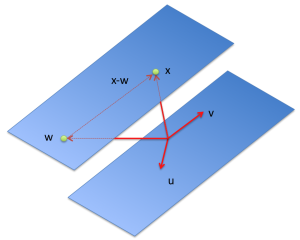
Nếu [latex]x_0 \in {\bf H}[/latex], thì với bất kỳ phần tử [latex]x \in {\bf H}[/latex] nào khác, chúng ta có
[latex]\begin{align*} b = a^Tx_0 = a^Tx. \end{align*}[/latex]
Do đó, siêu phẳng có thể được đặc trưng là tập hợp các vector [latex]x[/latex] sao cho [latex]x - x_0[/latex] trực giao với [latex]a[/latex]:
[latex]\begin{align*} \mathbf{H} = {x: a^T(x-x_0) = 0}. \end{align*}[/latex]
Siêu phẳng là các tập afin, có chiều [latex]n-1[/latex] (xem chứng minh ở đây). Do đó, chúng tổng quát hóa khái niệm thông thường về một mặt phẳng trong [latex]\mathbb{R}^3[/latex]. Siêu phẳng rất hữu ích vì chúng cho phép chia không gian thành hai vùng. Điều đó dẫn tới khái niệm về bán không gian.

Ví dụ 1: Một siêu phẳng trong [latex]\mathbb{R}^3[/latex]. [latexpage] Xét một tập afin có chiều (2) trong (\mathbb{R}^3), mà chúng ta mô tả là tập hợp các điểm (x) trong (\mathbb{R}^3) sao cho tồn tại hai tham số (\lambda_1, \lambda_2) sao cho [ x = \begin{pmatrix} 3\lambda_1-4\lambda_2 + 4 \ \lambda_1 \ \lambda_2 \end{pmatrix} = \begin{pmatrix} 4 \ 0 \ 0 \end{pmatrix} + \lambda_1 \begin{pmatrix} 3 \ 1 \ 0 \end{pmatrix} + \lambda_2 \begin{pmatrix} -4 \ 0 \ 1 \end{pmatrix}. ] Tập (\mathbf{H}) có thể được biểu diễn như một phép tịnh tiến của một không gian con tuyến tính: (\mathbf{H} = x_0 + \mathbf{L}), với [ x_0 := \begin{pmatrix} 4 \ 0 \ 0 \end{pmatrix}, ] và (\mathbf{L}) là không gian sinh bởi hai vector độc lập [ u := \begin{pmatrix} 3 \ 1 \ 0 \end{pmatrix}, \quad v := \begin{pmatrix} -4 \ 0 \ 1 \end{pmatrix}. ] Do đó, tập (\mathbf{H}) có chiều (2) trong (\mathbb{R}^3), do đó nó là một siêu phẳng. Trong (\mathbb{R}^3), siêu phẳng là các mặt phẳng thông thường. Chúng ta có thể tìm một biểu diễn của siêu phẳng ở dạng chuẩn [ \mathbf{H} = \left{ x ,:, a^T(x-x_0) = 0 \right}. ] Chúng ta chỉ cần tìm (a) vuông góc với cả (u) và (v). Tức là, chúng ta giải các phương trình [ 0 = a^T u = 3a_1 + a_2, \quad 0 = a^T v = -4a_1 + a_3. ] Điều trên dẫn đến (a = (a_1, -3a_1, 4a_1)). Chọn ví dụ (a_1 = 1) dẫn đến (a=(1,-3,4)).
		Siêu phẳng (\mathbf{H}) có thể được biểu diễn là (x_0 + \mathbf{span}(u, v)), trong đó (x_0) là một phần tử cụ thể, và (u, v) là hai vector độc lập. Tập (\mathbf{H}) được biểu diễn bằng màu xanh lam nhạt; nó là một phép tịnh tiến của không gian sinh tương ứng (\mathbf{L} = \mathbf{span}(u, v)). Bất kỳ điểm (x) nào trong (\mathbf{H}) đều thỏa mãn (x – x_0) thuộc (\mathbf{L}). Do đó, chúng ta có thể biểu diễn siêu phẳng là tập hợp các điểm sao cho (x – x_0) trực giao với (a), trong đó (a) là bất kỳ vector nào trực giao với cả (u, v).

5.2. Phép chiếu lên siêu phẳng

Xét siêu phẳng [latex]{\bf H} = {x: a^Tx = b}[/latex], và giả sử không mất tính tổng quát rằng [latex]a[/latex] đã được chuẩn hóa ([latex]||a||2 =1[/latex]). Chúng ta có thể biểu diễn [latex]{\bf H}[/latex] là tập hợp các điểm [latex]x[/latex] sao cho [latex]x- x_0[/latex] trực giao với [latex]a[/latex], trong đó [latex]x_0[/latex] là bất kỳ vector nào trong [latex]{\bf H}[/latex], tức là sao cho [latex]a^Tx_0 = b[/latex]. Một vector như vậy là [latex]x{proj}:= ba[/latex].

Theo cấu trúc, [latex]x_{proj}[/latex] là phép chiếu của [latex]0[/latex] lên [latex]{\bf H}[/latex]. Tức là, nó là điểm trên [latex]{\bf H}[/latex] gần gốc tọa độ nhất, vì nó giải bài toán chiếu
[latex]\begin{align*} \min\limits_x ||x||_2: x \in \mathbf{H} \end{align*}[/latex]
Thật vậy, với bất kỳ [latex]x \in {\bf H}[/latex] nào, sử dụng bất đẳng thức Cauchy-Schwartz:
[latex]\begin{align*} ||x_0||_2 = |b| = |a^Tx| \leq ||a||_2 \cdot ||x||_2 = ||x||2, \end{align*}[/latex]
và độ dài nhỏ nhất |[latex]b[/latex]| đạt được với [latex]x{proj} = ba[/latex].

5.3. Hình học của siêu phẳng

5.4. Bán không gian

Một bán không gian là một tập hợp con của [latex]\mathbb{R}^n[/latex] được xác định bằng một bất đẳng thức duy nhất liên quan đến một tích vô hướng. Chính xác hơn, một nửa không gian trong [latex]\mathbb{R}^n[/latex] là một tập hợp có dạng
[latex]\begin{align*} \mathbf{H} = {x: a^Tx \ge b}, \end{align*}[/latex]
trong đó [latex]a \in \mathbb{R}^n[/latex], [latex]a \neq 0[/latex], và [latex]b \in \mathbb{R}[/latex] được cho.

Về mặt hình học, nửa không gian ở trên là tập hợp các điểm sao cho [latex]{a^T(x-x_0) \ge 0[/latex], tức là, góc giữa [latex]x - x_0[/latex] và [latex]a[/latex] là góc nhọn (trong [latex][-90^{\circ}; +90^{\circ}][/latex]). Ở đây [latex]x_0[/latex] là điểm gần gốc tọa độ nhất trên siêu phẳng được xác định bởi đẳng thức [latex]a^Tx = b[/latex]. (Khi [latex]a[/latex] đã được chuẩn hóa, như trong hình, [latex]x_0 = ba[/latex].)

	Bán không gian [latex]{x: a^Tx \ge b},[/latex] là tập hợp các điểm sao cho [latex]x-x_0[/latex] tạo thành một góc nhọn với [latex]a[/latex], trong đó [latex]x_0[/latex] là phép chiếu của gốc tọa độ lên biên của nửa không gian.
	Hình bên trái mô tả một bán không gian trong trường hợp không gian ba chiều.