Gradient của một hàm khả vi [latex]f:\mathbb{R}^n \rightarrow \mathbb{R}[/latex] chứa các đạo hàm cấp một của hàm số theo mỗi biến. Gradient hữu ích để tìm xấp xỉ tuyến tính của hàm số gần một điểm.
Định nghĩa
Gradient của [latex]f[/latex] tại [latex]x_0[/latex], ký hiệu là [latex]\nabla f(x_0)[/latex], là véctơ trong [latex]\mathbb{R}^n[/latex] được cho bởi
[latex]\nabla f\left(x_0\right) = \begin{pmatrix} \dfrac{\partial f}{\partial x_1}(x_0) \\[0.5em] \vdots \\[0.5em] \dfrac{\partial f}{\partial x_n}(x_0) \end{pmatrix}.[/latex]
Ví dụ:
● Hàm khoảng cách:
Hàm khoảng cách từ một điểm [latex]p \in \mathbb{R}^2[/latex] đến một điểm khác [latex]x \in \mathbb{R}^2[/latex] được định nghĩa là
$$
\rho(x)=\|x-p\|_2=\sqrt{\left(x_1-p_1\right)^2+\left(x_2-p_2\right)^2} .
$$
Hàm số này khả vi, với điều kiện [latex]x \neq p[/latex], điều mà ta giả sử. Khi đó
$$
\nabla \rho(x)=\frac{1}{\sqrt{\left(x_1-p_1\right)^2+\left(x_2-p_2\right)^2}}\left(\begin{array}{l}
x_1-p_1 \\
x_2-p_2
\end{array}\right) .
$$
● Hàm log-sum-exp: Xét hàm “log-sum-exp” [latex]\operatorname{lse}: \mathbb{R}^2 \rightarrow \mathbb{R}[/latex], với các giá trị
$$
\operatorname{lse}(x):=\log \left(e^{x_1}+e^{x_2}\right) .
$$
Gradient của [latex]\operatorname{lse}[/latex] tại [latex]x[/latex] là
$$
\nabla \operatorname{lse}(x)=\frac{1}{z_1+z_2}\left(\begin{array}{c}
z_1 \\
z_2
\end{array}\right) .
$$
trong đó [latex]z_i:=e^{x_i}, i=1,2[/latex]. Tổng quát hơn, gradient của hàm [latex]\operatorname{lse}: \mathbb{R}^n \rightarrow \mathbb{R}[/latex] với các giá trị
$$
\operatorname{lse}(x)=\log \left(\sum_{i=1}^n e^{x_i}\right)
$$
được cho bởi
$$
\nabla f(x)=\frac{1}{\sum_{i=1}^n e^{x_i}}\left(\begin{array}{c}
e^{x_1} \\
\ldots \\
e^{x_n}
\end{array}\right)=\frac{1}{Z} z,
$$
trong đó \(z=\left(e^{x_1}, \ldots, e^{x_n}\right)\), và \(Z=\sum_{i=1}^n z_i\).
Quy tắc hợp với một ánh xạ afin
Nếu [latex]A \in \mathbb{R}^{m \times n}[/latex] là một ma trận, và [latex]b \in \mathbb{R}^m[/latex] là một véctơ, hàm [latex]g: \mathbb{R}^n \rightarrow \mathbb{R}[/latex] với các giá trị
$$
g(x)=f(A x+b)
$$
được gọi là hàm hợp của ánh xạ afin [latex]x \rightarrow A x+b[/latex] với [latex]f[/latex]. Gradient của nó được cho bởi (xem chứng minh tại đây)
$$
\nabla g(x)=A^T \nabla f(A x+b) .
$$
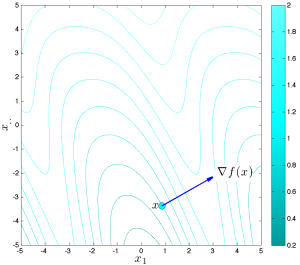
Diễn giải hình học
Về mặt hình học, gradient có thể được đọc trên đồ thị của đường mức của hàm số. Cụ thể, tại một điểm [latex]x[/latex] bất kỳ, gradient vuông góc với đường mức và hướng ra ngoài từ tập mức dưới (tức là, nó hướng về phía các giá trị lớn hơn của hàm số).
 |
Các đường mức và tập mức dưới của hàm [latex]f:\mathbb{R}^2 \rightarrow \mathbb{R}[/latex] với các giá trị \[ Gradient tại một điểm (hiển thị màu đỏ) vuông góc với đường mức, và hướng ra ngoài tập mức dưới tương ứng. Độ dài của gradient xác định tốc độ thay đổi cục bộ của hàm số (Độ dài của gradient đã được phóng to lên [latex]5[/latex] lần.) |
