27
27.1. Bài tập cơ bản
[latexpage]
\textit{Chính quy hóa cho dữ liệu nhiễu.} Xét một bài toán bình phương tối thiểu
\[ \min _x\|A x-y\|_2^2 \]
trong đó ma trận dữ liệu $A \in \mathbb{R}^{m \times n}$ bị nhiễu. Mô hình nhiễu cụ thể của chúng ta giả định rằng mỗi hàng $a_i^T \in \mathbb{R}^n$ có dạng $a_i=\hat{a}_i+u_i$, trong đó véctơ nhiễu $u_i \in \mathbb{R}^n$ có trung bình không và ma trận hiệp phương sai là $\sigma^2I_n$, với $\sigma$ là một thước đo độ lớn của nhiễu. Do đó, bây giờ ma trận $A$ là một hàm của tập hợp các véctơ bất định $u=\left(u_1, \ldots, u_m\right)$, mà ta ký hiệu là $A(u)$. Ta sẽ viết $\hat{A}$ để ký hiệu ma trận có các hàng là $\hat{a}_i^T, \; i=1, \ldots, m$. Ta thay thế bài toán ban đầu bằng
\[ \min _x \mathbf{E}_u\|A(u) x-y\|_2^2 \]
trong đó $\mathbf{E}_u$ ký hiệu giá trị kỳ vọng đối với biến ngẫu nhiên $u$. Chứng minh rằng bài toán này có thể được viết dưới dạng
\[ \min_x \|\hat{A}x-y\|_2^2 + \lambda \|x\|_2^2 \]
trong đó $\lambda \ge 0$ là một tham số chính quy hóa nào đó, mà ta sẽ xác định. Tức là, bình phương tối thiểu chính quy hóa có thể được diễn giải là một cách để tính đến các sự bất định trong ma trận $A$, theo nghĩa giá trị kỳ vọng.
\textit{Gợi ý:} tính giá trị kỳ vọng của $((\hat{a}_i+u_i)^Tx-y_i)^2$, với một chỉ số hàng $i$ cụ thể.
27.2. Ứng dụng
 |
Hình vẽ cho thấy số lượng transistor trong 13 vi xử lý như một hàm của năm ra mắt của chúng. Đồ thị cho thấy rằng ta có thể thu được một sự khớp tốt với một hàm có dạng $n(t)=\alpha^{t-t_0}$, trong đó $t$ là năm, $n(t)$ là số lượng transistor tại năm $t$, và $\alpha>0$ và $t_0$ là các tham số của mô hình. Mô hình này cho kết quả là một đường thẳng nếu ta vẽ $n(t)$ trên thang đo logarit và $t$ trên thang đo tuyến tính, như được thực hiện trong hình. |
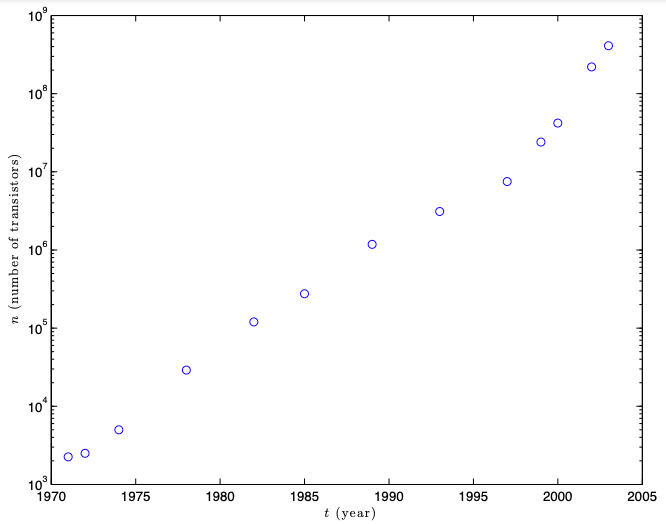
1. Định luật Moore’s mô tả một xu hướng dài hạn trong lịch sử của phần cứng máy tính và phát biểu rằng số lượng transistor có thể được đặt một cách không tốn kém trên một mạch tích hợp đã tăng gấp đôi xấp xỉ mỗi hai năm. Trong bài toán này, ta khảo sát tính hợp lệ của phát biểu này thông qua bình phương tối thiểu.
Chỉ ra cách ước lượng các tham số $\alpha, t_0$ sử dụng bình phương tối thiểu, tức là, thông qua một bài toán có dạng
\[ \min _x\|A x-y\|_2 \]
Hãy định nghĩa chính xác dữ liệu $A,y$ và mối liên hệ giữa biến $x$ với các tham số ban đầu của bài toán là $\alpha, t_0$. (Sử dụng các ký hiệu $n=(n_1, \ldots, n_{13}) \in \mathbb{R}^{13}$ cho số lượng transistor, và $t=(t_1, \ldots, t_{13}) \in \mathbb{R}^{13}$ cho các năm tương ứng. Ta có thể giả sử rằng không có thành phần nào của $x$ bằng không tại điểm tối ưu.)
a. Nghiệm của bài toán trên có duy nhất không? Giải thích cẩn thận câu trả lời của bạn, và đưa ra biểu thức cho nghiệm duy nhất $x^*$ theo $A,y$.
b. Nghiệm của bài toán cho kết quả $\alpha=1.4257, t_0=1949.7$. Ước lượng này có phù hợp với định luật Moore, vốn phát biểu rằng số lượng transistor trên mỗi mạch tích hợp tăng gần gấp đôi mỗi hai năm không?
2. Mô hình Michaelis–Menten cho động học enzyme liên hệ tốc độ của một phản ứng enzyme, $y$, với nồng độ của một cơ chất, $x$, như sau:
\[ y=\frac{\beta_1 x}{\beta_2+x} \]
trong đó $\beta_i, i=1,2$, là các tham số.
a. Chứng minh rằng mô hình có thể được biểu diễn như một mối quan hệ tuyến tính giữa các giá trị $1/y$ và $1/x$.
b. Sử dụng biểu thức này để khớp tham số $\beta$ bằng cách sử dụng bình phương tối thiểu tuyến tính.
c. Phương pháp trên đã được nhận thấy là khá nhạy cảm với sai số trong dữ liệu đầu vào. Liệu có thể xác nhận ý kiến này bằng thực nghiệm không?
\textit{Gợi ý:} tạo dữ liệu nhiễu từ các giá trị tham số $\beta_1=3.4$ và $\beta_2=0.4$.
