Định nghĩa

Định thức của một ma trận vuông [latex]A[/latex] kích thước [latex]n \times n[/latex], ký hiệu là [latex]\det A[/latex], được định nghĩa bằng một công thức đại số của các hệ số trong [latex]A[/latex]. Công thức sau đây cho định thức, được biết đến là công thức khai triển Laplace, cho phép tính định thức một cách quy nạp:

[latex]\begin{align*} \det A &= \sum\limits_{i=1}^n (-1)^{i+1} A_{i,1} \det(C_i), \end{align*}[/latex]

trong đó [latex]A_{i,1}[/latex] là ma trận [latex](n-1) \times (n-1)[/latex] thu được từ [latex]A[/latex] bằng cách bỏ đi hàng thứ [latex]i[/latex] và cột đầu tiên. (Cột đầu tiên không có nhiều ý nghĩa ở đây, vì định thức không đổi nếu chúng ta sử dụng bất kỳ cột nào khác.)

Định thức là hàm duy nhất của các phần tử trong [latex]A[/latex] sao cho

1. [latex]\det I = 1[/latex].

2. Ánh xạ [latex]A \rightarrow \det A[/latex] là một hàm tuyến tính theo mỗi cột (khi các cột khác được giữ cố định).

3. [latex]\det A[/latex] đổi dấu khi hai cột được hoán vị.

Có những biểu thức khác của định thức, bao gồm công thức Leibnitz (chứng minh ở đây):

[latex]\begin{align*} \det A &= \sum\limits_{\sigma \in S_n} {\bf sign}(\sigma) A_{\sigma(i), i} \end{align*}[/latex]

trong đó [latex]S_n[/latex] ký hiệu tập hợp các hoán vị [latex]\sigma[/latex] của các số nguyên [latex]1,2, \cdots, n[/latex]. Ở đây, [latex]{\bf sign}(\sigma)[/latex] ký hiệu dấu của hoán vị [latex]\sigma[/latex], là số lần tráo đổi cặp để biến đổi [latex]\sigma(1), \sigma(2), \cdots, \sigma(n)[/latex] thành [latex]1, 2, \cdots, n[/latex].

Kết quả quan trọng

Một kết quả quan trọng là một ma trận vuông khả nghịch khi và chỉ khi định thức của nó khác không. Chúng ta sử dụng kết quả chính này khi giới thiệu các trị riêng của ma trận đối xứng.

Ý nghĩa hình học

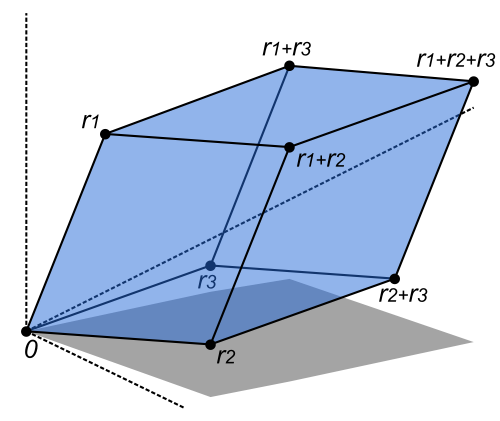	Định thức của một ma trận [latex]3 \times 3[/latex] [latex]A[/latex] với các cột [latex]r_1, r_2, r_3[/latex] là thể tích của hình hộp được xác định bởi các véctơ [latex]r_1, r_2, r_3[/latex]. (Nguồn: wikipedia). Do đó, định thức là một thước đo tỷ lệ để định lượng cách ánh xạ tuyến tính liên quan đến [latex]A, x \rightarrow Ax[/latex], làm thay đổi thể tích.

Nói chung, giá trị tuyệt đối của định thức của một ma trận [latex]n \times n[/latex] là thể tích của hình hộp

[latex]\begin{align*} \{Ax: 0\leq x_i \leq 1, \quad i = 1, \dots, n\}. \end{align*}[/latex]

Thật vậy, khi [latex]A[/latex] không khả nghịch, các cột của nó xác định một hình hộp có thể tích bằng không.

Định thức và nghịch đảo

Định thức có thể được sử dụng để tính ma trận nghịch đảo của một ma trận vuông, hạng đầy đủ (tức là khả nghịch) [latex]A[/latex]: ma trận nghịch đảo [latex]B=A^{-1}[/latex] có các phần tử được cho bởi

[latex]\begin{align*} B_{ij} &= \frac{(-1)^{i+j}}{\det A} \det (\tilde{A}_{ij}), \end{align*}[/latex]

trong đó [latex]\tilde{A}_{ij}[/latex] là một ma trận thu được từ [latex]A[/latex] bằng cách bỏ đi hàng thứ [latex]i[/latex] và cột thứ [latex]j[/latex]. Ví dụ, định thức của một ma trận [latex]2 \times 2[/latex]

[latex]\begin{align*} A &= \left(\begin{array}{ll} a & b \\ c & d \end{array}\right) \end{align*}[/latex]

được cho bởi

[latex]\begin{align*} \det A &= ad-bc. \end{align*}[/latex]

Nó chính là diện tích của hình bình hành được xác định bởi các cột của [latex]A[/latex], [latex](a,c),(b,d)[/latex]. Ma trận nghịch đảo được cho bởi

[latex]\begin{align*} A^{-1} &= \frac{1}{ad-bc} \left(\begin{array}{cc} \phantom{-}d & -b \\ -c & \phantom{-}a \end{array}\right) \end{align*} [/latex]

Một số tính chất

Định thức của ma trận tam giác

Nếu một ma trận là ma trận tam giác vuông, thì định thức của nó đơn giản là tích của các hệ số trên đường chéo. Điều này xuất phát trực tiếp từ công thức khai triển Laplace ở trên.

Định thức của ma trận chuyển vị

Định thức của một ma trận vuông và của ma trận chuyển vị của nó là bằng nhau.

Định thức của một tích các ma trận

Đối với hai ma trận vuông khả nghịch, ta có

[latex]\begin{align*} \det AB &= \det A \cdot \det B. \end{align*}[/latex]

Cụ thể:

[latex]\begin{align*} \det A^{-1} &= \frac{1}{\det A}. \end{align*}[/latex]

Điều này cũng suy ra rằng đối với một ma trận trực giao [latex]U[/latex], tức là một ma trận [latex]n \times n[/latex] với [latex]U^TU = I[/latex], ta có

[latex]\begin{align*} 1 &= \det U^TU = (\det U^T) \det U = (\det U)^2. \end{align*}[/latex]

Định thức của ma trận khối

Một sự tổng quát hóa của kết quả trên, ta có ba khối tương thích [latex]A, C, D[/latex]:

Một công thức tổng quát hơn là