39
[latexpage]
39.1 Nén ảnh.
Biểu diễn ảnh dưới dạng ma trận
Ta có thể biểu diễn ảnh dưới dạng ma trận như sau. Xét một hình ảnh có [latex]n \times m[/latex] điểm ảnh. Đối với ảnh thang độ xám, ta cần một số cho mỗi điểm ảnh, có thể được biểu diễn dưới dạng một ma trận [latex]n \times m[/latex]. Đối với ảnh màu, ta cần ba số cho mỗi điểm ảnh, cho mỗi màu: đỏ, lục và lam (RGB). Mỗi màu có thể được biểu diễn dưới dạng một ma trận [latex]n \times m[/latex], và ta có thể biểu diễn ảnh màu đầy đủ dưới dạng một ma trận [latex]n \times 3m[/latex], trong đó ta xếp chồng ma trận của mỗi màu theo cột bên cạnh nhau, như sau
\[ A = \begin{bmatrix} A_{\text{red}} & A_{\text{green}} & A_{\text{blue}} \end{bmatrix}. \]
 |
Hình ảnh bên trái là một ảnh thang độ xám, có thể được biểu diễn dưới dạng một ma trận [latex]298 \times 298[/latex] chứa các giá trị thang độ xám được lưu trữ dưới dạng số nguyên. |
Hình ảnh cũng có thể được trực quan hóa. Trước tiên, ta phải chuyển đổi ma trận từ số nguyên sang số thực dấu phẩy động. Ở định dạng JPEG, hình ảnh sẽ được tải vào matlab dưới dạng một mảng ba chiều, một ma trận cho mỗi màu. Đối với ảnh thang độ xám, ta chỉ cần ma trận đầu tiên trong mảng.
Xấp xỉ hạng thấp
Sử dụng phương pháp xấp xỉ hạng thấp thông qua SVD, ta có thể tạo ra các xấp xỉ hạng-[latex]k[/latex] tốt nhất cho ma trận.
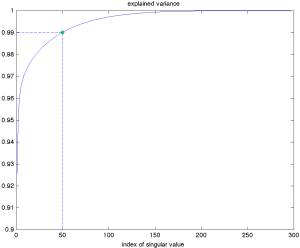
Ảnh gốc và ảnh xấp xỉ, với các hạng khác nhau. Ta quan sát thấy rằng với [latex]k=50[/latex], phép xấp xỉ gần như giống hệt với ảnh gốc, có hạng là [latex]r = m = n = 298[/latex].
Nhắc lại rằng phương sai giải thích được của xấp xỉ hạng-[latex]k[/latex] là tỷ lệ giữa bình phương chuẩn của ma trận xấp xỉ hạng-[latex]k[/latex] và bình phương chuẩn của ma trận gốc. Về cơ bản, nó đo lường lượng thông tin được giữ lại trong phép xấp xỉ so với bản gốc.
 |
Phương sai giải thích được cho các xấp xỉ hạng-[latex]k[/latex] khác nhau của ảnh gốc cung cấp cái nhìn sâu sắc về chất lượng của phép xấp xỉ. Với [latex]k=50[/latex], phép xấp xỉ chứa hơn 99% tổng phương sai trong ảnh, cho thấy rằng xấp xỉ hạng-50 gần như không thể phân biệt được với bản gốc về mặt nội dung thông tin. |
39.2 Phân tích dữ liệu thị trường.
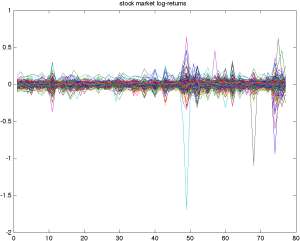
Ta xem xét logarit tỷ suất sinh lợi hàng ngày của một tập hợp gồm [latex]77[/latex] cổ phiếu được chọn trong các công ty Fortune 100 trong khoảng thời gian từ ngày 3 tháng 1 năm 2007 đến ngày 31 tháng 12 năm 2008. Ta có thể biểu diễn điều này dưới dạng một ma trận [latex]77 \times 504[/latex], với mỗi cột là một ngày, và mỗi hàng là một chuỗi thời gian tương ứng với một cổ phiếu cụ thể.
 |
Hình ảnh bên trái biểu diễn chuỗi thời gian của thị trường chứng khoán đã đề cập ở trên, được hiển thị dưới dạng một tập hợp các chuỗi thời gian. Ta lưu ý rằng logarit tỷ suất sinh lợi dao động quanh một giá trị trung bình dường như gần bằng không. |
 |
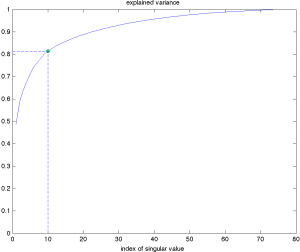Ta có thể thực hiện phân tích SVD của ma trận logarit tỷ suất sinh lợi, và vẽ đồ thị phương sai giải thích được. Ta thấy rằng 10 giá trị kỳ dị đầu tiên giải thích hơn 80% phương sai của dữ liệu. |
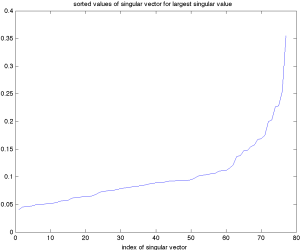Việc xem xét véctơ kỳ dị tương ứng với giá trị kỳ dị lớn nhất, được sắp xếp theo thứ tự tăng dần, rất có ý nghĩa. Ta quan sát thấy rằng tất cả các thành phần đều có cùng dấu (mà ta luôn có thể giả sử là dương). Điều này có nghĩa là ta có thể diễn giải véctơ này như là cung cấp một giá trị trung bình có trọng số của thị trường. Như đã thấy trong đồ thị trước, xấp xỉ hạng một tương ứng giải thích gần đúng hơn 80% phương sai trong dữ liệu thị trường này, điều này minh chứng cho câu nói “trung bình thị trường chi phối thị trường”. Năm thành phần có độ lớn lớn nhất tương ứng với các công ty sau. Lưu ý rằng tất cả đều là các công ty tài chính:
- FABC (Fidelity Advisor)
- FTU (Wachovia, bought by Wells Fargo)
- MER (Merrill Lynch, đã được Bank of America mua lại)
- AIG (don’t need to elaborate)
- MS (Morgan Stanley)
